目录
写出正确代码
-
定义清楚循环不变量
-
维护循环不变量
-
定义清楚函数功能
LinearSearch 输入: 数组 和 目标元素 输出: 目标元素所在的索引;若不存在返回 -1
复杂度分析
复杂度分析: 表示算法的性能 通常看最坏的情况 算法运行的上界
选择排序法
每次选择还没处理的最小元素,放到已处理的最后面
如何原地完成?不开辟新数组
i 指向已处理的最后一个元素 j 指向还没处理的第一个元素 minIndex 指向未处理的最小元素 arr[i, n) 是还没处理的元素 在 arr[i, n) 中找到最小的元素,放到 arr[i] 的位置
算法复杂度 O(n^2)
数据结构
数组
把数据码成一排进行存放
- 数组最大的优点:快速查询,scores[2]
新增和删除都是 O(n) 改/删除 已知索引 O(1), 未知 O(n)
栈
栈是一种后进先出的数据结构
应用: Undo(撤销) 操作 程序调用的系统栈
数组实现的栈: 进栈出栈的时间复杂度都是 O(1)
队列
队列也是一种线性数据结构,先进先出 只能从队尾插入,队首取出
数组实现的队列
进(队尾添加) O(1) 出(队首出,后续向前挪一位) O(n)
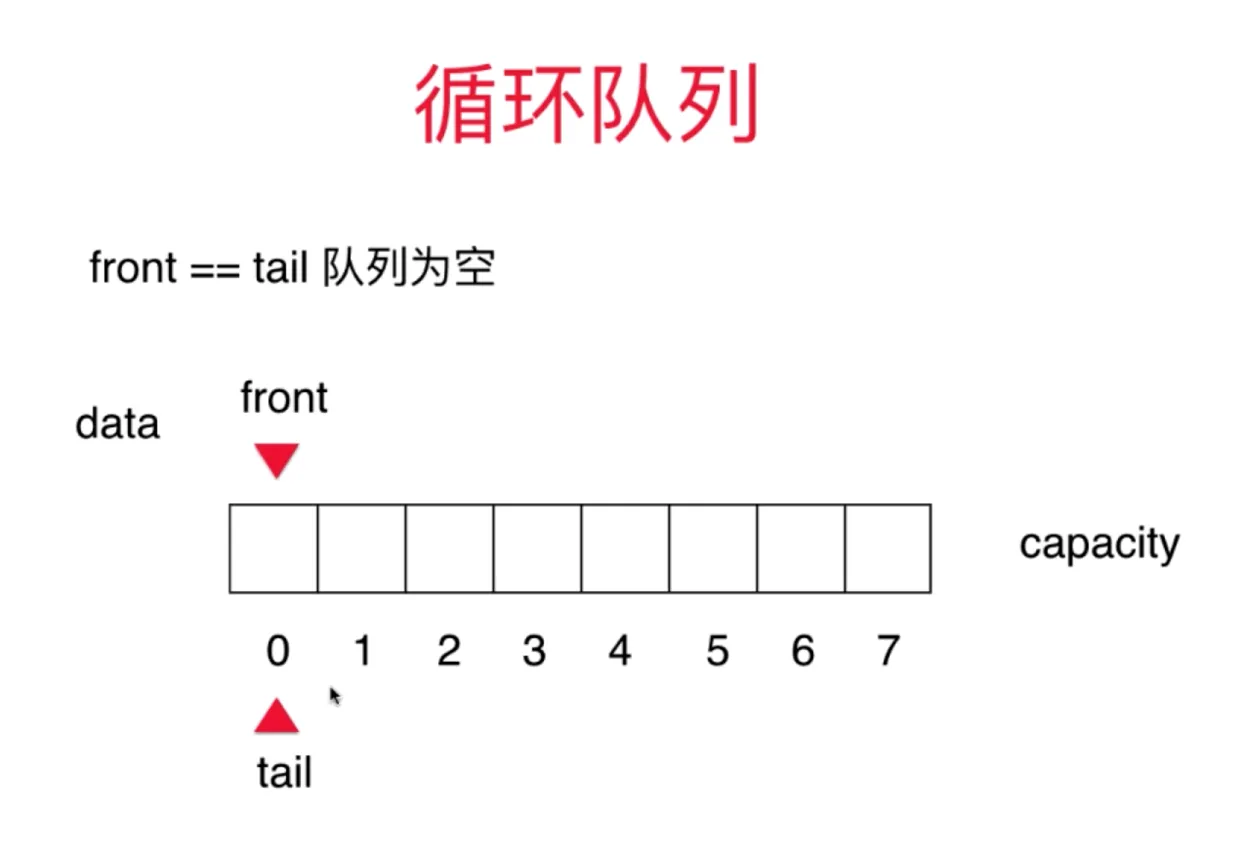
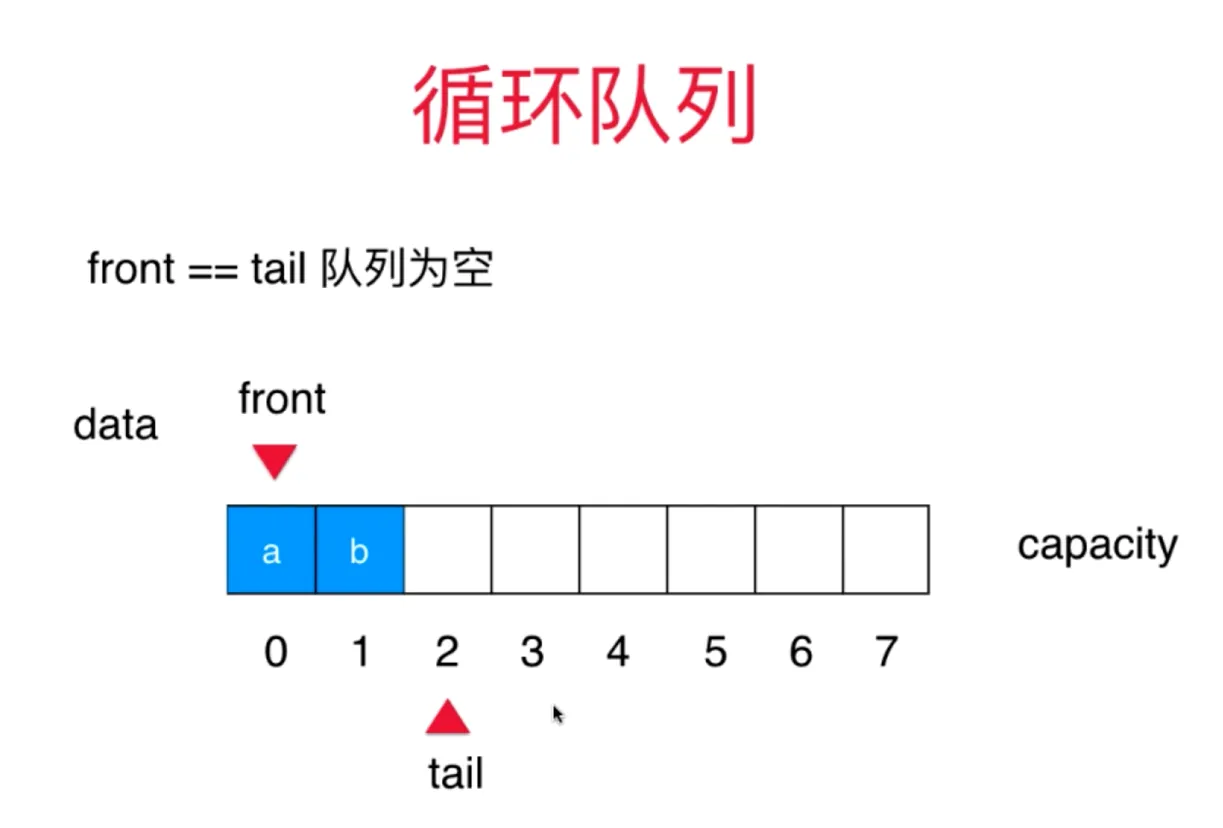
循环数组实现的队列
思路 一个数组 front 指向队首 tail 指向队尾
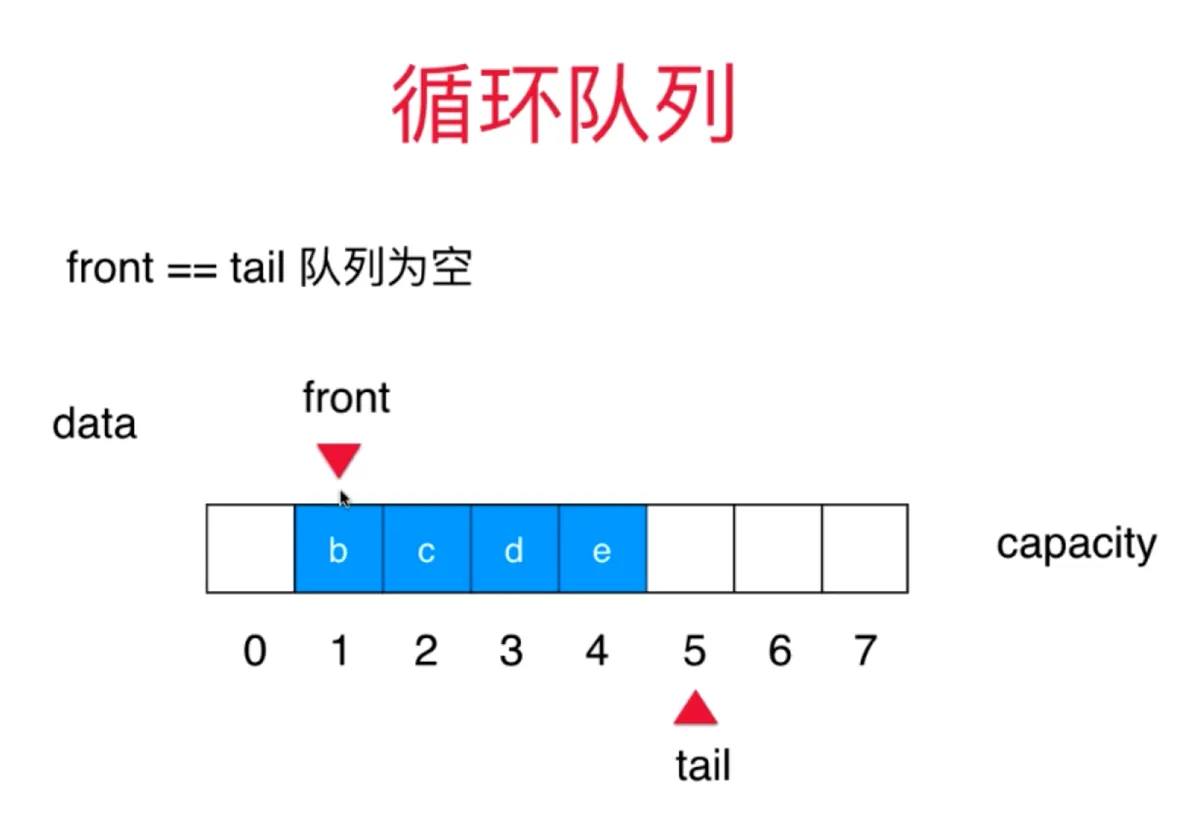
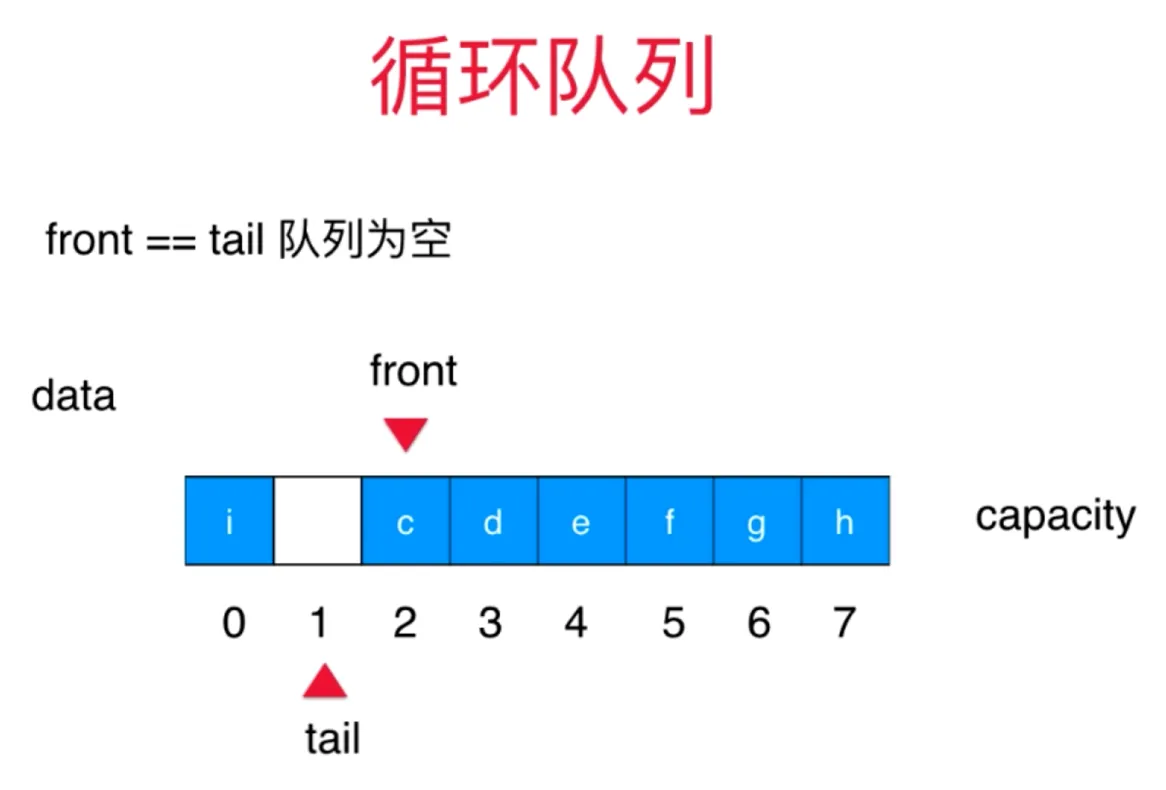
front==tail 时候队列为空 入队时,(tail+1) % capacity 出队时, front - 1 当 tail 到容量上限时,且队首有空时(队列未满) tail 指向队首 (tail + 1) % capacity = front 时候队列满 队列满时始终有一个元素为空
可自动扩容
进(队尾添加) O(1) 出(队首出) O(1)
todo:
- 使用 size 不浪费一个空间
- 浪费一个空间,不使用 size
- 新双端队列(Deque),可以在队首和队尾添加/删除元素 addFront removeFront addLast removeLast
使用栈实现队列 232 使用队列实现栈 225
链表 linked list
数据存储在“节点”(Node)中 优点:真正的动态,不需要处理固定容量的问题 缺点:丧失了随机访问的能力
在链表的 index (0-based) 位置添加新元素e
- 链表最好维护了一个虚拟头节点
- prev 节点,指向虚拟头节点,往后遍历到 index 位置,这个位置就是待插入的前一位 比如 0->1->2->3->4 在 index=2 处插入 9,即插入到 1 和 2 的中间,由于虚拟头节点存在 内部指向为 dummyHead->0->1->2->3->4, 那 prev 就是从 dummyHead 往后挪 index 位(从0开始) prev=1 Node(9).next = prev.next 即 9->2->3->4 prev.next = Node(9) 即 dummyHead->0->1->9->2->3->4
添加操作 O(n) addLast O(n) addFirst O(1) add O(n/2)=O(n) 删除 O(n) 查找 O(n)
使用链表实现栈
链表头部增删复杂度都是 O(1)
使用链表实现队列
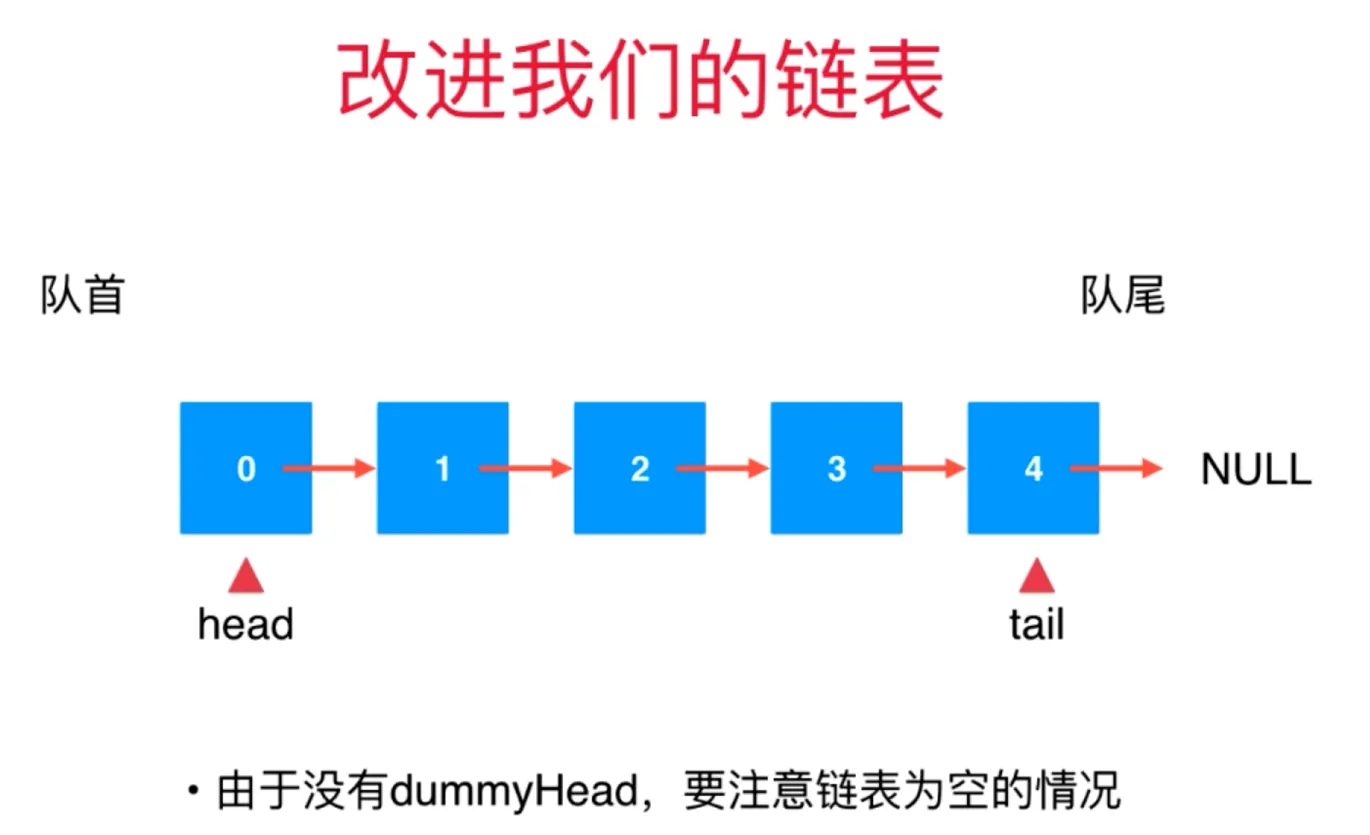
需要加一个尾指针 tail, 指向最后一个元素
3->2->1->0->NULL
从尾部添加元素的复杂度是 O(1), 无法根据 tail 指针来删除(只指向后一个元素)
故队列从链表 尾部插入,头部删除,均是 O(1)
反转链表
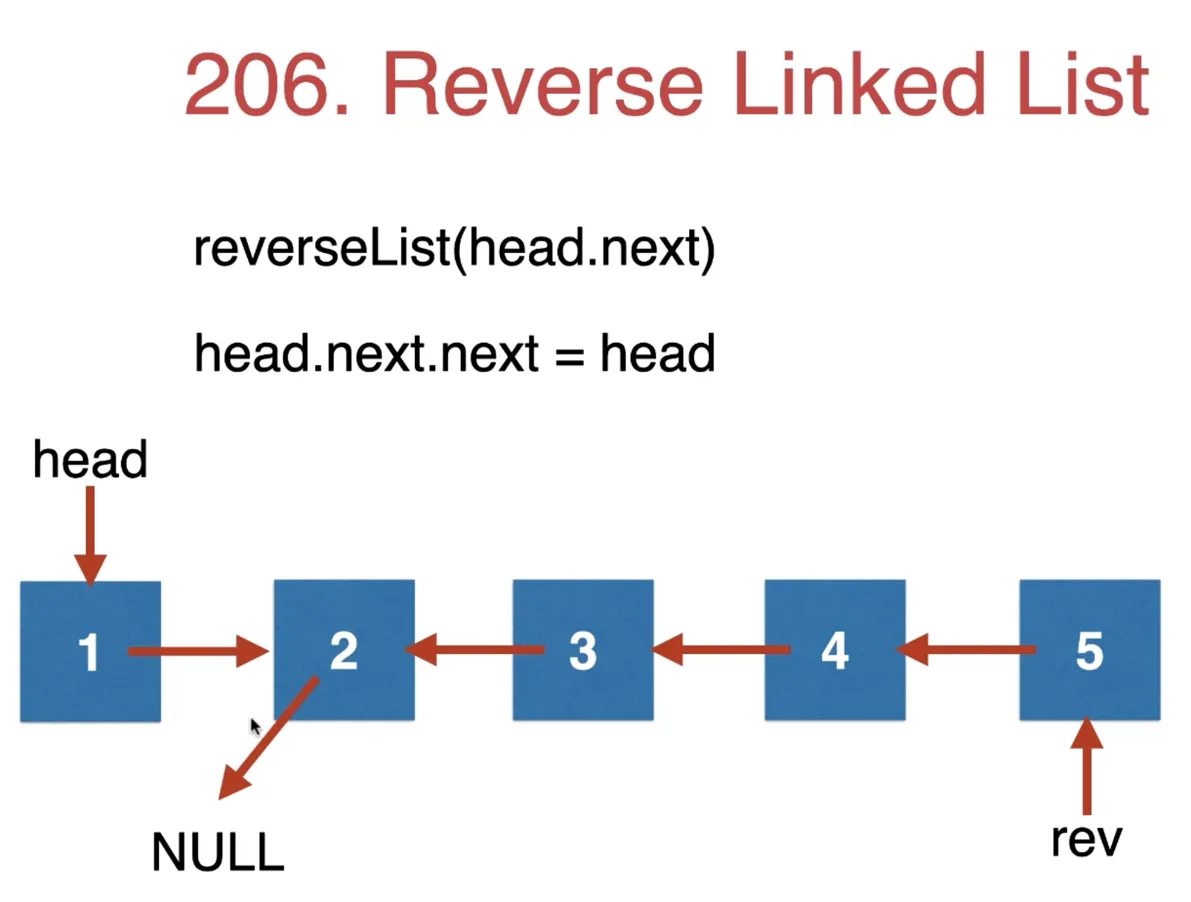
递归实现
reverseList(head.next) 时可以认为后面都已经反转结束了 函数返回的是反转后的头节点
此时 head 仍然指向的是,反转后的最末尾节点 head.next = 最末尾节点 所以,我们让反转后节点,最末尾节点的 next 指向 head 就是 (head.next).next = head
选择排序
先把最小的拿出来,放到第一个位置,然后再从剩下的里面找最小的,放到第二个位置,以此类推 原地排序
func selectionSort[T constraints.Ordered](data []T) {
// i 指向已处理的最后一个元素
// j 指向还没处理的第一个元素
// minIndex 指向未处理的最小元素
for i := 0; i < len(arr); i++ {
minIndex := i
for j := i + 1; j < len(arr); j++ {
if arr[j] < arr[minIndex] {
minIndex = j
}
}
arr[i], arr[minIndex] = arr[minIndex], arr[i]
}
}时间复杂度 O(n^2)
插入排序法
arr[0, i) 是有序的,arr[i, n) 是无序的 i 指向已经处理了的元素,从 0 开始,每次循环,把 arr[i] 插入到 arr[0, i) 的合适位置 (合适位置的计算方式: 从后往前比较,如果比前一个小,就交换位置,直到比前一个大,或者到了第一个位置)
public class InsertionSort<E> {
public static <E extends Comparable<E>> void sort(E[] arr) {
for (int i = 1; i < arr.length; i++) {
E temp = arr[i];
int j;
for (j = i; j > 0; j--) {
if (temp.compareTo(arr[j - 1]) < 0) {
E tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
} else {
break;
}
}
arr[j] = temp;
}
}
}
优化: 交换操作改为赋值操作
public static <E extends Comparable<E>> void sort(E[] arr) {
for (int i = 1; i < arr.length; i++) {
E temp = arr[i];
int j;
for (j = i; j - 1 > 0 && temp.compareTo(arr[j - 1]) < 0; j--) {
arr[j] = arr[j - 1];
}
arr[j] = temp;
}
}时间复杂度 O(n^2) 初始状态下,数组是有序的,那么时间复杂度是 O(n)
归并排序
把需要排序的数组,一份为二,分别对子数组排序,然后把这两个排序后的子数组合并为一个即可 子数组的排序是同样的思路 MergeSort(arr, l, r) 对 arr 的 [l, r] 部分排序
MergeSort(arr, l, r) { if (l >= r) return int mid = (l + r) / 2; // 对 arr[l, mid] 排序 MergeSort(arr, l, mid) // 对 arr[mid, r] 排序 MergeSort(arr, mid, r) // 将 arr[l, mid] 和 arr[mid, r] 合并 merge(arr, l, mid, r) }
merge(arr, l, mid, r) 的过程
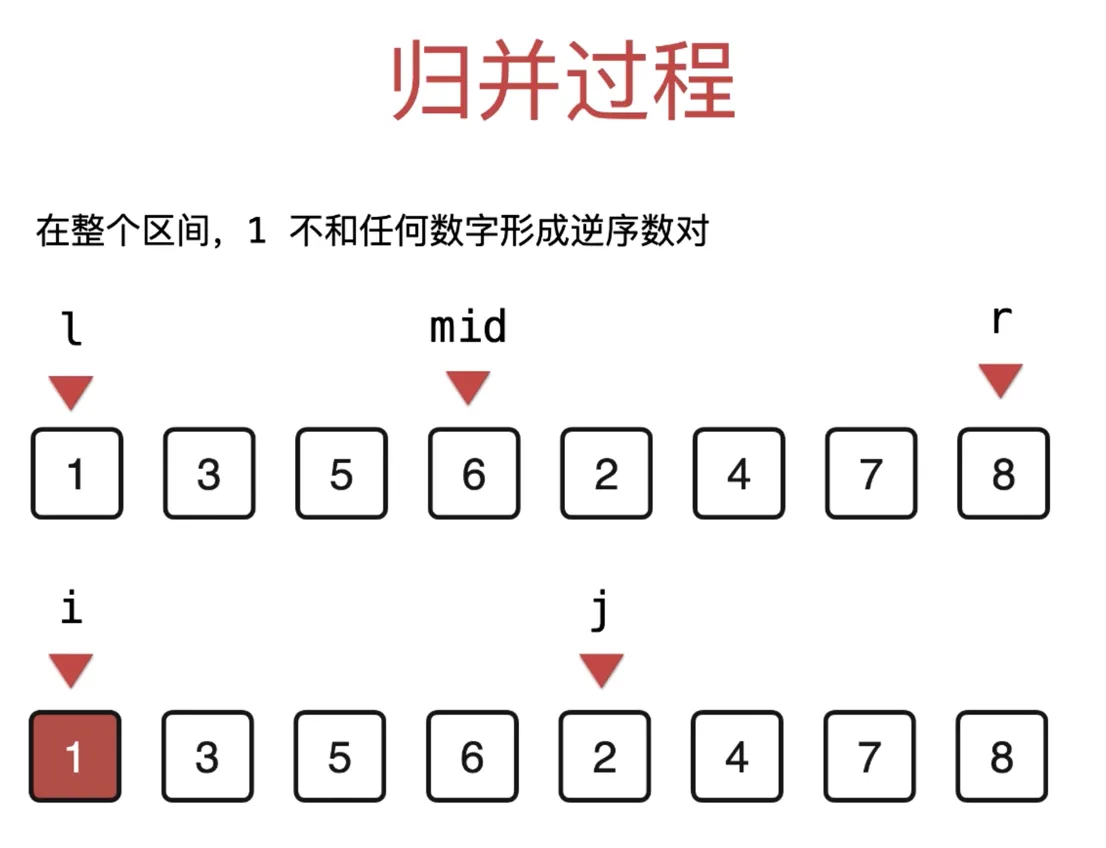
当前指针如下, arr[l:mid] 有序, arr[mid+1:r] 有序
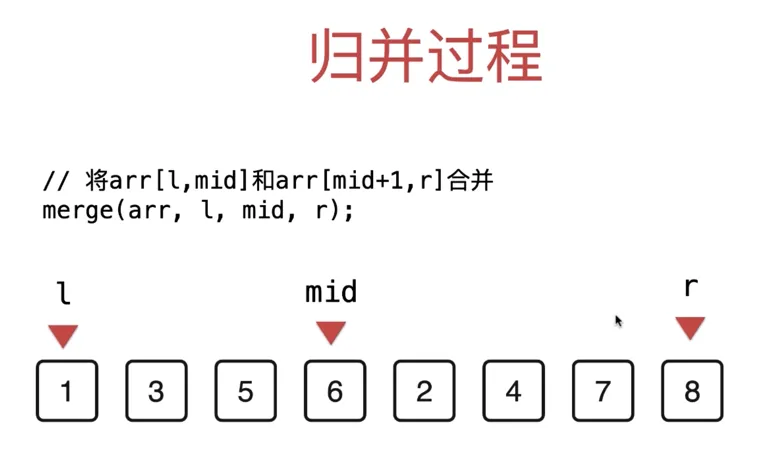 复制一个新的数组 tmp
i 初始指向第一个区间的第一个元素 (i = l)
j 初始指向第二个区间的第一个元素 (j = mid+1)
复制一个新的数组 tmp
i 初始指向第一个区间的第一个元素 (i = l)
j 初始指向第二个区间的第一个元素 (j = mid+1)
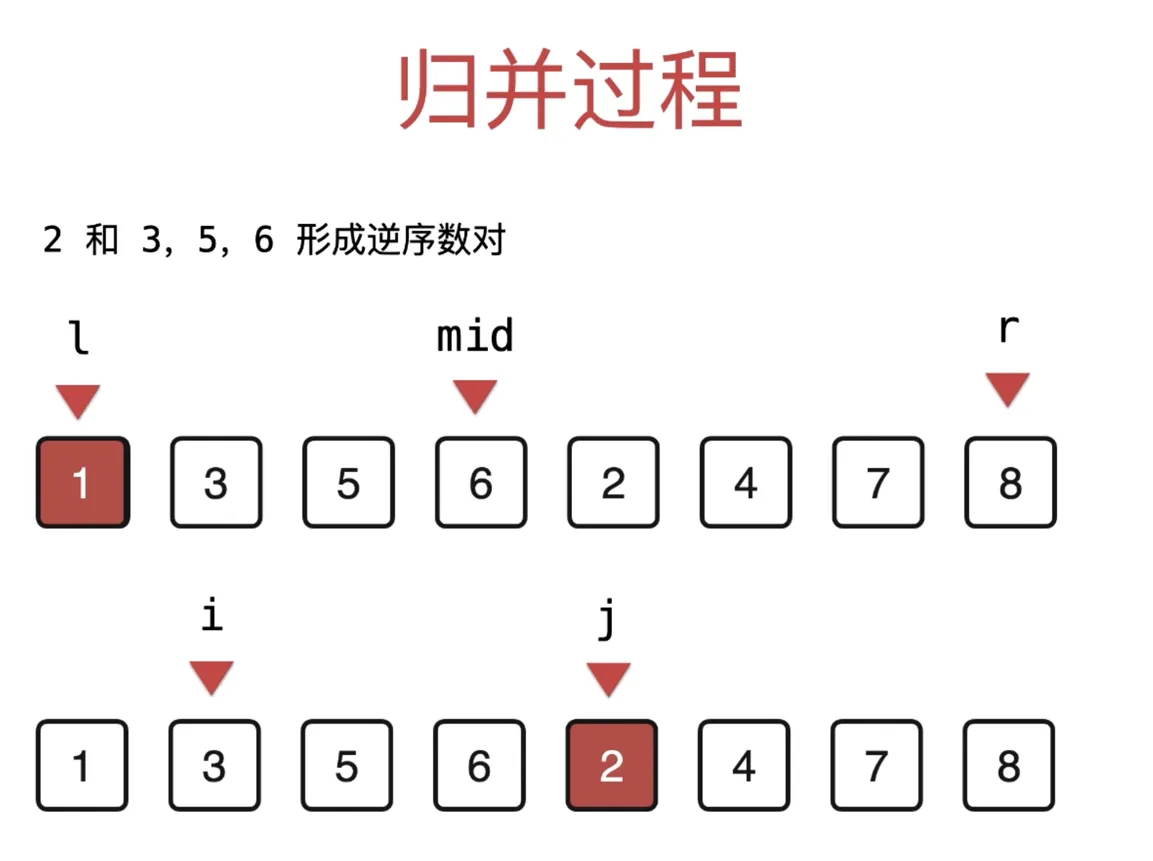
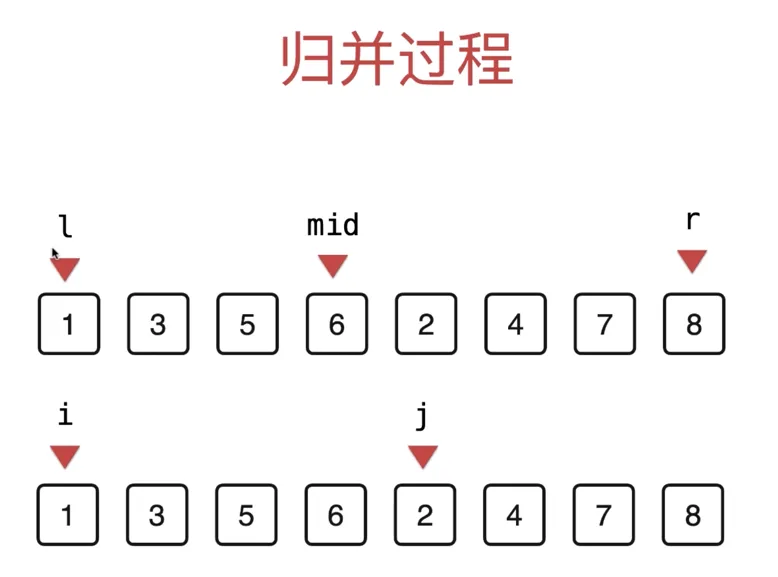 把 i,j 中指向的最小的值复制到上面的数组中,对应指针+1
把 i,j 中指向的最小的值复制到上面的数组中,对应指针+1
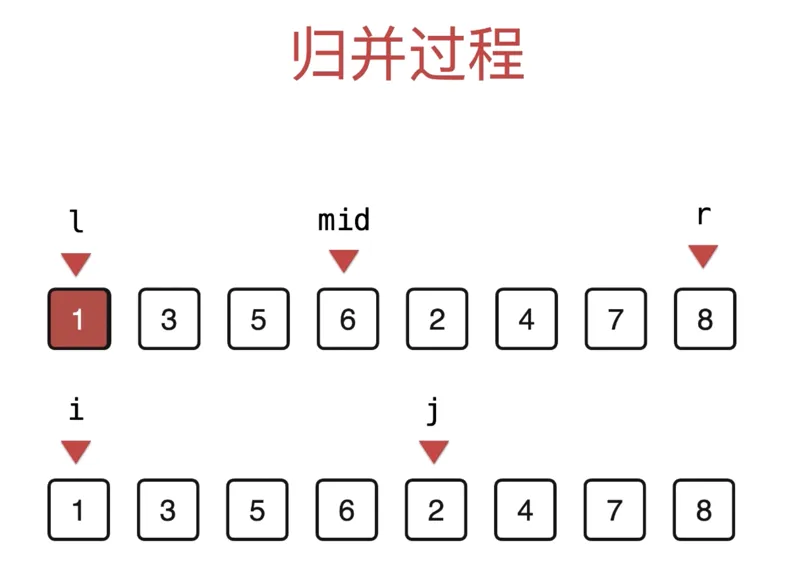
归并的过程无法原地完成
算法复杂度:O(nlogn)
优化1: 如果 arr[mid] < arr[mid + 1],则说明 arr[l:mid] 和 arr[mid+1:r] 已经有序,不需要 merge
private static <E extends Comparable<E>> void sort(E[] arr, int l, int r) {
if (l >= r) {
return;
}
// 下面写法是为了防止整形溢出
int mid = l + (r - l) / 2;
sort(arr, l, mid);
sort(arr, mid + 1, r);
if (arr[mid].compareTo(arr[mid + 1]) > 0) {
// 优化1:如果 arr[mid] < arr[mid + 1],则说明 arr[l:mid] 和 arr[mid+1:r] 已经有序,不需要 merge
merge(arr, l, mid, r);
}
}对于有序的数组,归并排序的时间复杂度是 O(n)
优化2: 当数据规模小于 15 时,使用算法复杂度为O(n^2)的归并排序
private static <E extends Comparable<E>> void insertSort(E[] arr, int l, int r) {
for (int i = l + 1; i <= r; i++) {
E temp = arr[i];
int j;
for (j = i; j > l && temp.compareTo(arr[j - 1]) < 0; j--) {
arr[j] = arr[j - 1];
}
arr[j] = temp;
}
}
private static <E extends Comparable<E>> void sort(E[] arr, int l, int r) {
if (l >= r) {
return;
}
// 优化2:当数据规模小于 15 时,使用算法复杂度为O(n^2)的归并排序
if (r - l <= 15) {
insertSort(arr, l, r);
return;
}
// 下面写法是为了防止整形溢出
int mid = l + (r - l) / 2;
sort(arr, l, mid);
sort(arr, mid + 1, r);
if (arr[mid].compareTo(arr[mid + 1]) > 0) {
// 优化1:如果 arr[mid] < arr[mid + 1],则说明 arr[l:mid] 和 arr[mid+1:r] 已经有序,不需要 merge
merge(arr, l, mid, r);
}
}这个优化在某些解释执行语言中,可能不会有太大的提升,因为函数调用的开销比较大
优化3: 内存占用优化,merge 的时候,之前写法每次都开辟一个新数组,新的写法是,在初次调用的时候就创建这个数组 后续的 merge 操作,都是在这个数组上进行操作
private static <E extends Comparable<E>> void merge(E[] arr, int l, int mid, int r, E[] temp) {
// 把 arr 中的 l 到 r 区间的元素复制到 temp 中
System.arraycopy(arr, l, temp, l, r - l + 1);
int i = l, j = mid + 1;
// 每轮循环为 arr[k] 赋值
for (int k = l; k <= r; k++) {
if (i > mid) {
// 左区间已经全部处理完毕
arr[k] = temp[j];
j++;
} else if (j > r) {
// 右区间已经全部处理完毕
arr[k] = temp[i];
i++;
} else if (temp[i].compareTo(temp[j]) < 0) {
// 左区间更小
arr[k] = temp[i];
i++;
} else {
// 右区间更小
arr[k] = temp[j];
j++;
}
}
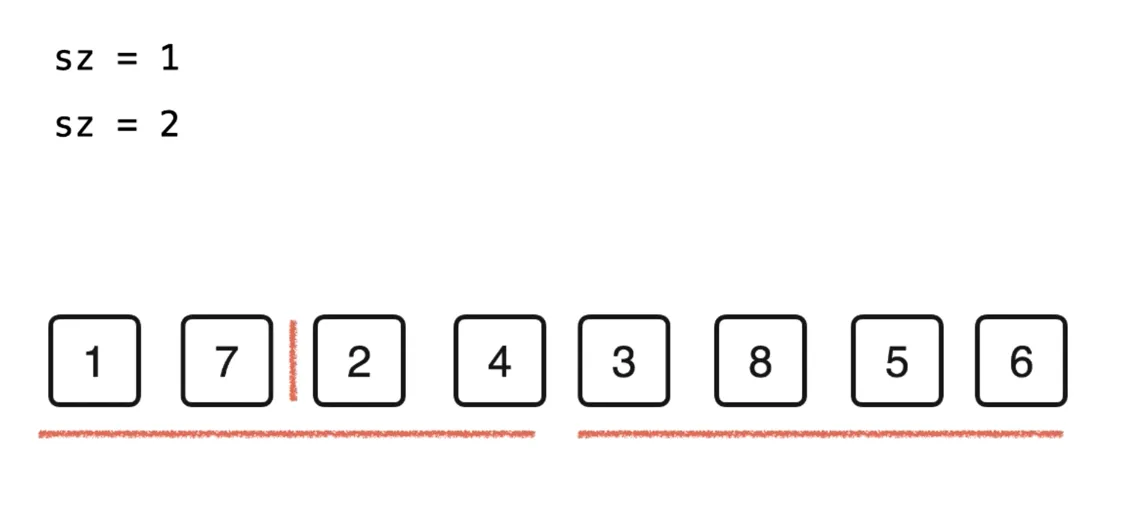
}自底向上的归并排序
-
把每两个元素分为一组 size(sz)=1
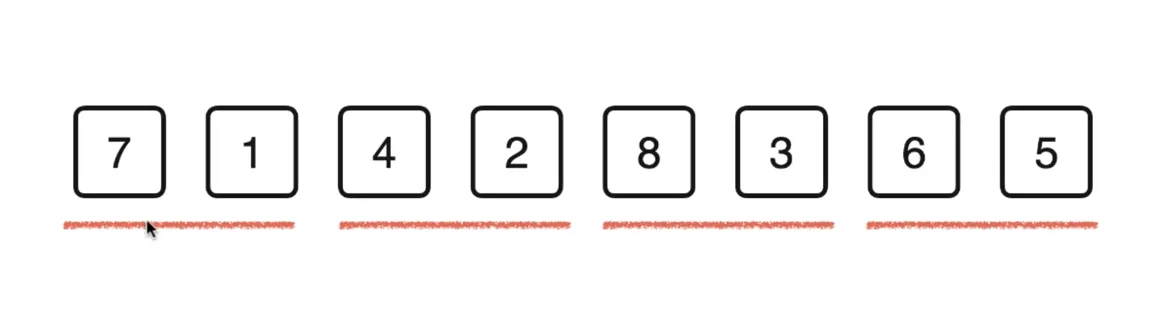
-
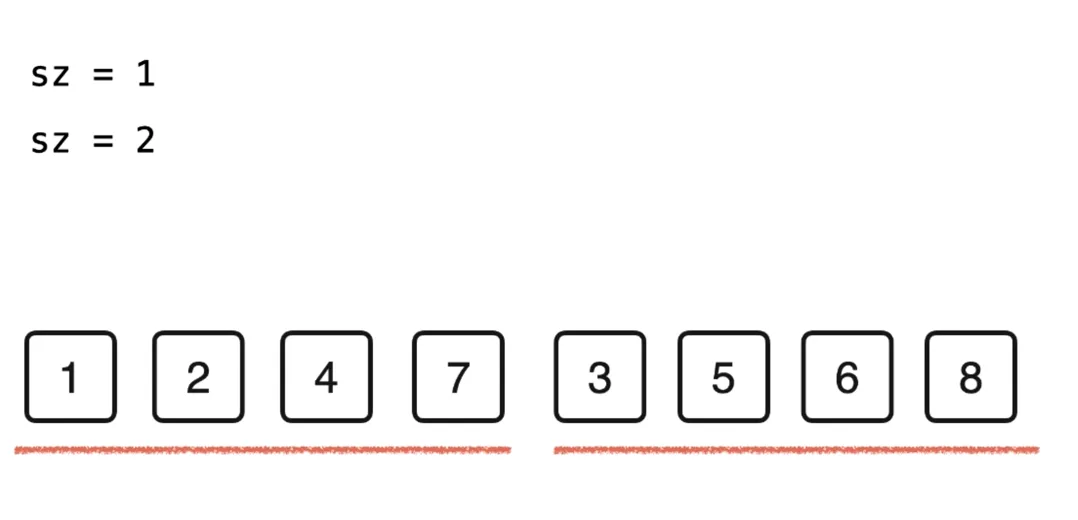
对这两个包含一个元素的有序数据进行归并排序,得到一个长度为 2 的有序数组
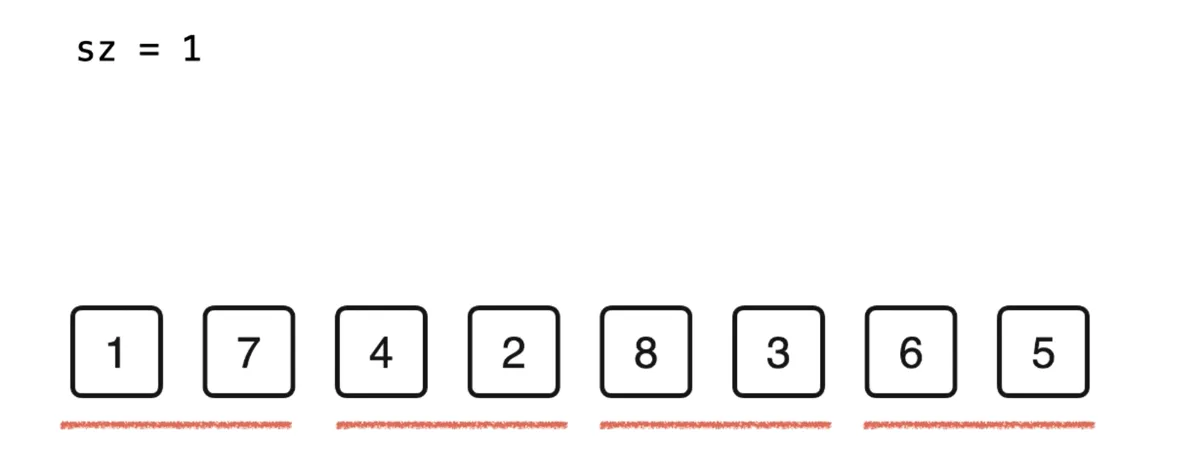
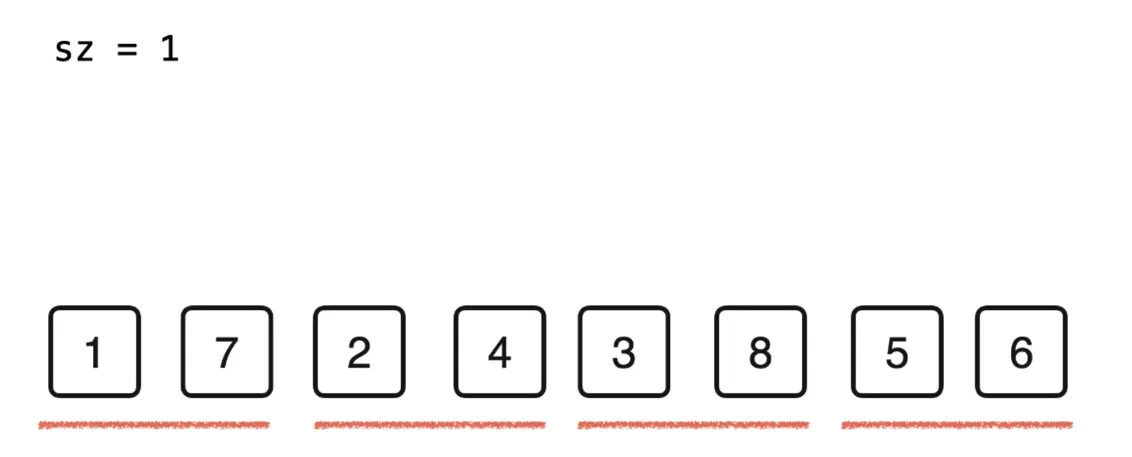
-
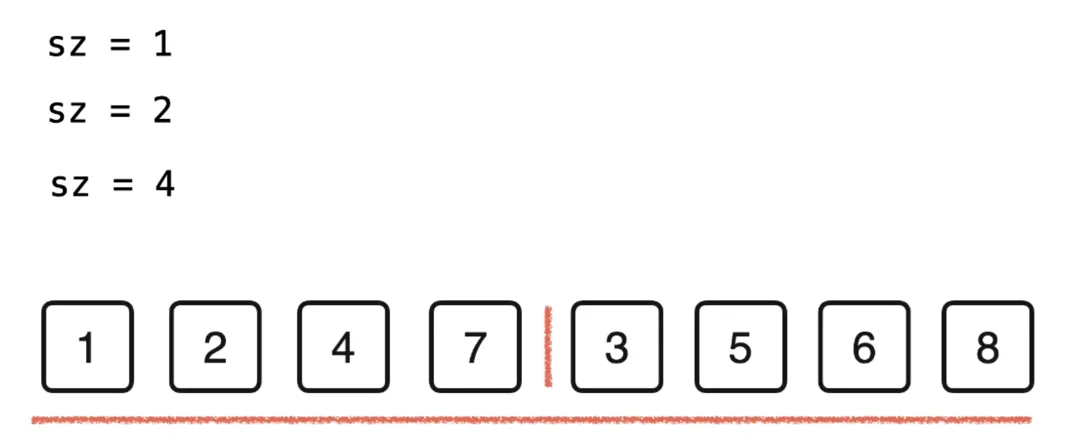
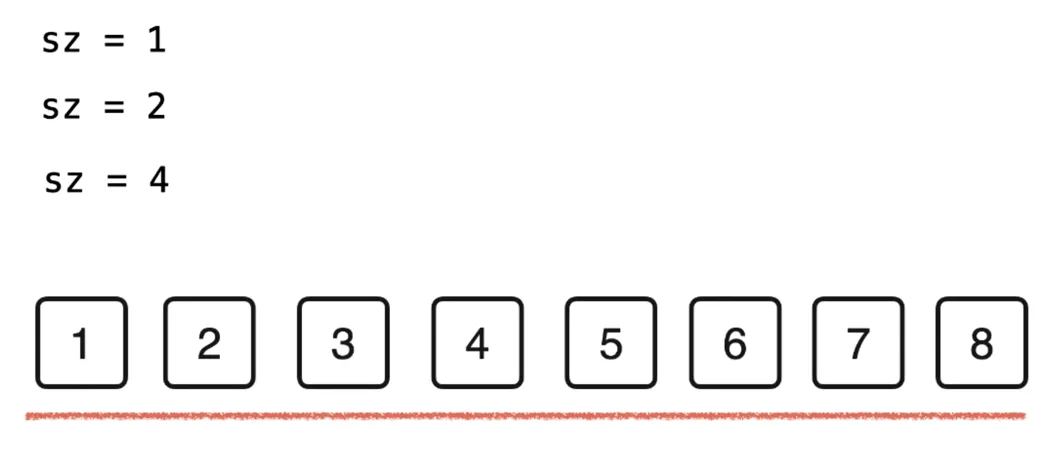
继续对排序后的有序数组进行归并
// 自底向上的归并排序
public static <E extends Comparable<E>> void sortBU(E[] arr) {
E[] temp = Arrays.copyOf(arr, arr.length);
int n = arr.length;
// 遍历合并的区间长度
for (int sz = 1; sz < n; sz += sz) {
// 遍历合并的两个区间的起始位置 i
// 合并 [i, i+sz-1] 和 [i+sz, i+sz+sz-1]
for (int i = 0; i + sz < n; i += sz + sz) {
if (arr[i + sz - 1].compareTo(arr[i + sz]) > 0) {
// 当前面的区间大于后面时,才执行归并操作,否则就已经是有序的了
int r = Math.min(i + sz + sz - 1, n - 1);
merge(arr, i, i + sz - 1, r, temp);
}
}
}
}
LCR 170. 交易逆序对的总数
快速排序
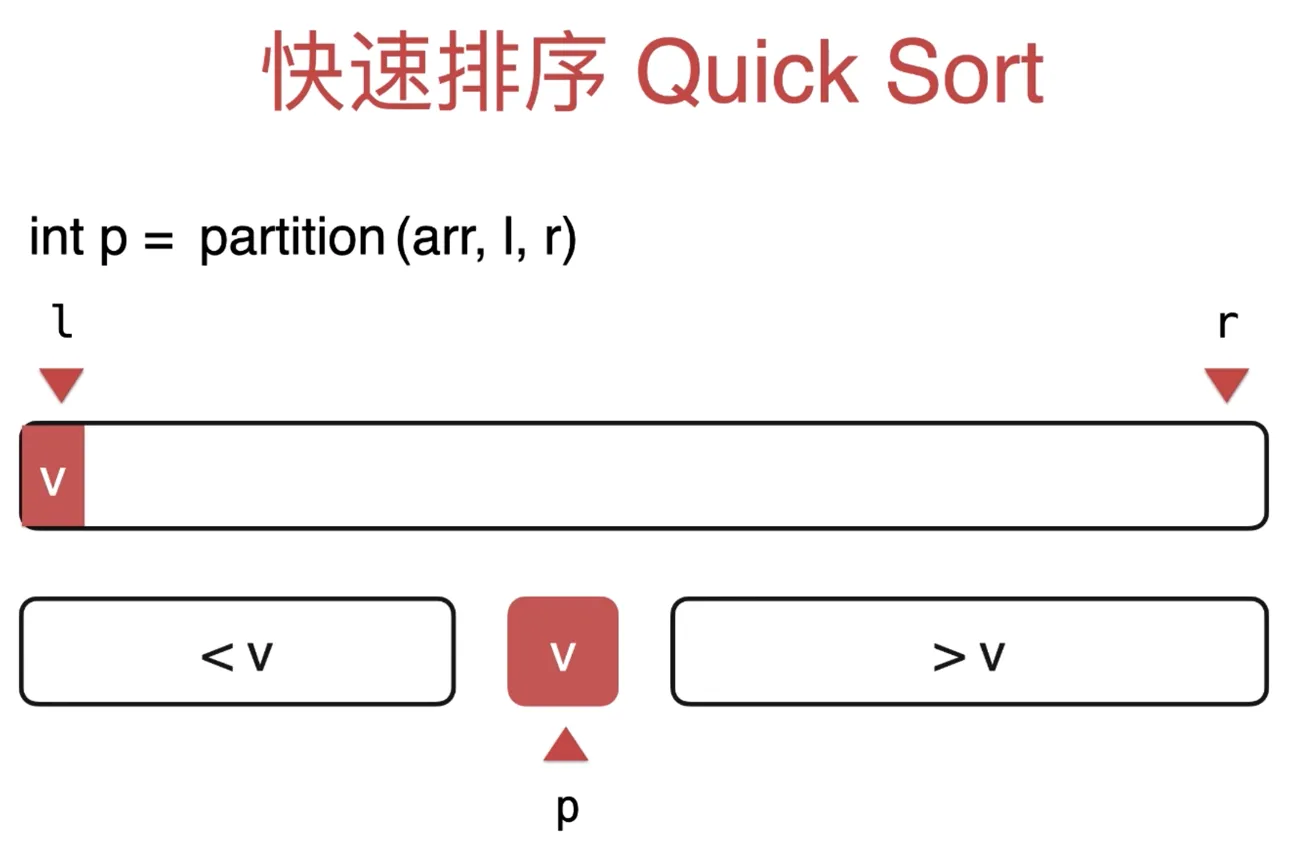
选择数组[l, r]第一个元素 v 作为标定点,
执行 int p = partition(arr, l, r) 函数
把数组分为三部分,左边为小于 v, 中间为 v, 右边大于 v(暂时不考虑等于v)
返回值的 p 是一个索引,对应 v 标定点所在位置

计算 partition
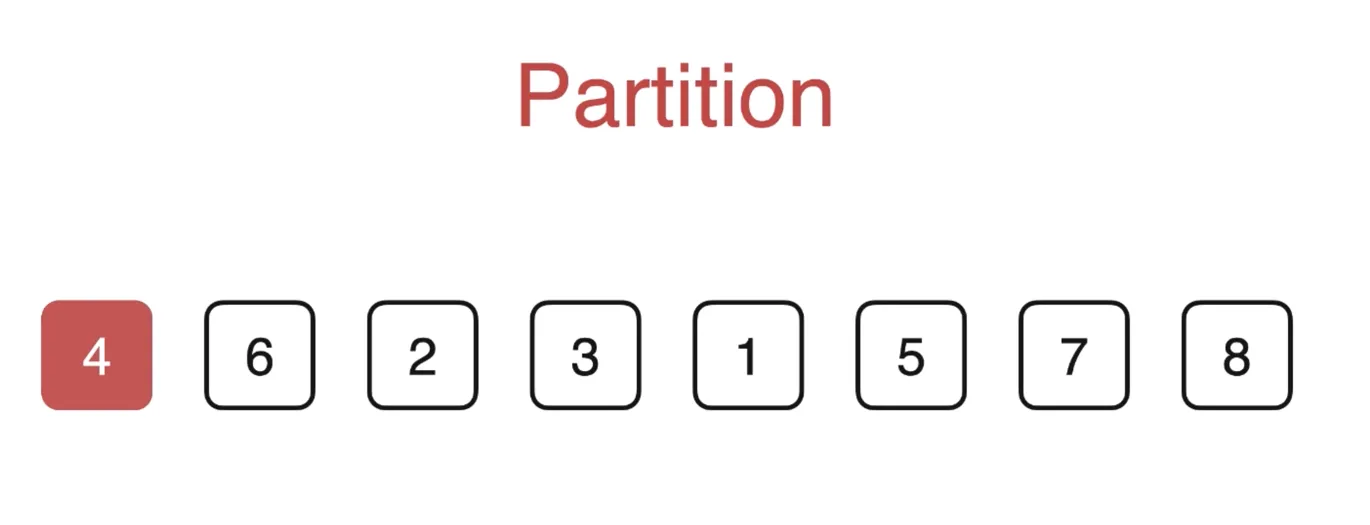
如果允许开辟空间
使用额外两个数组,小于 v 放 left, 大于 v 放 right,就完成了
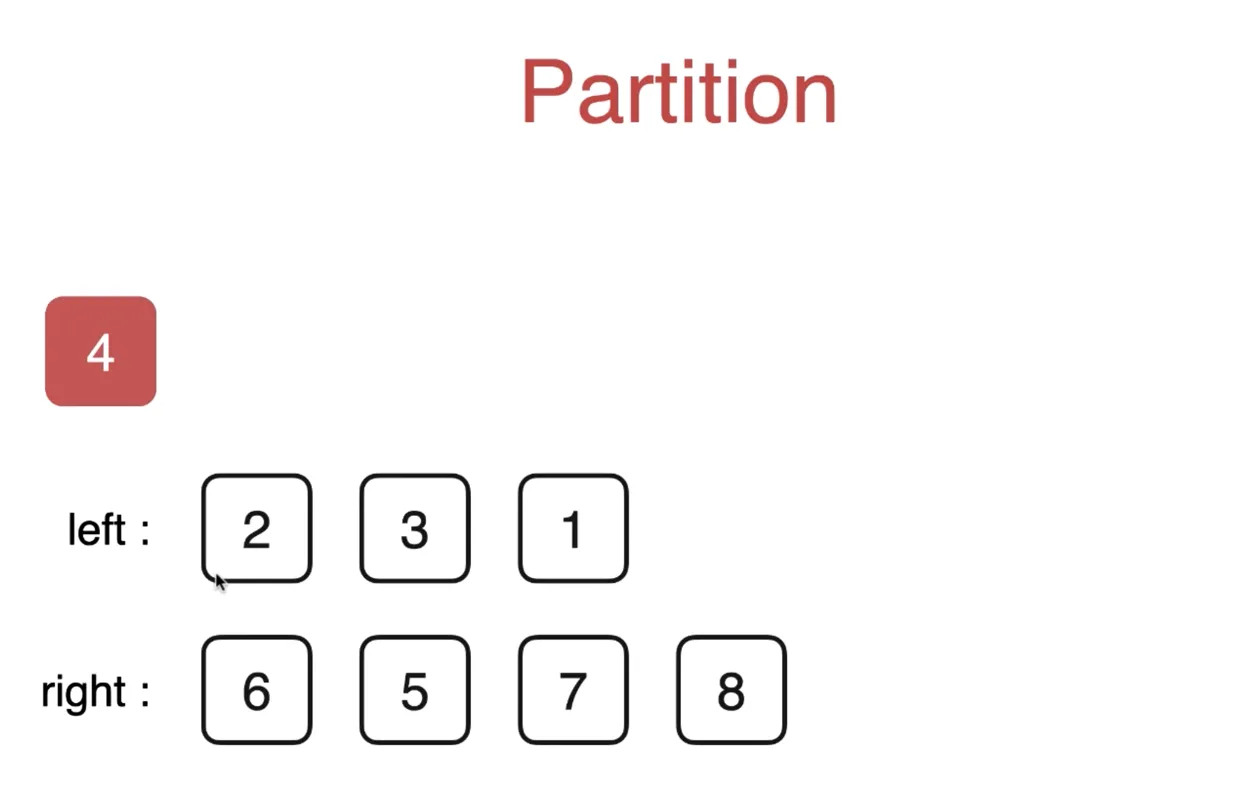
原地排序
取第一个元素v, j 指向小于 v 和大于 v 所在位置的索引
i指向未整理的最近一个元素
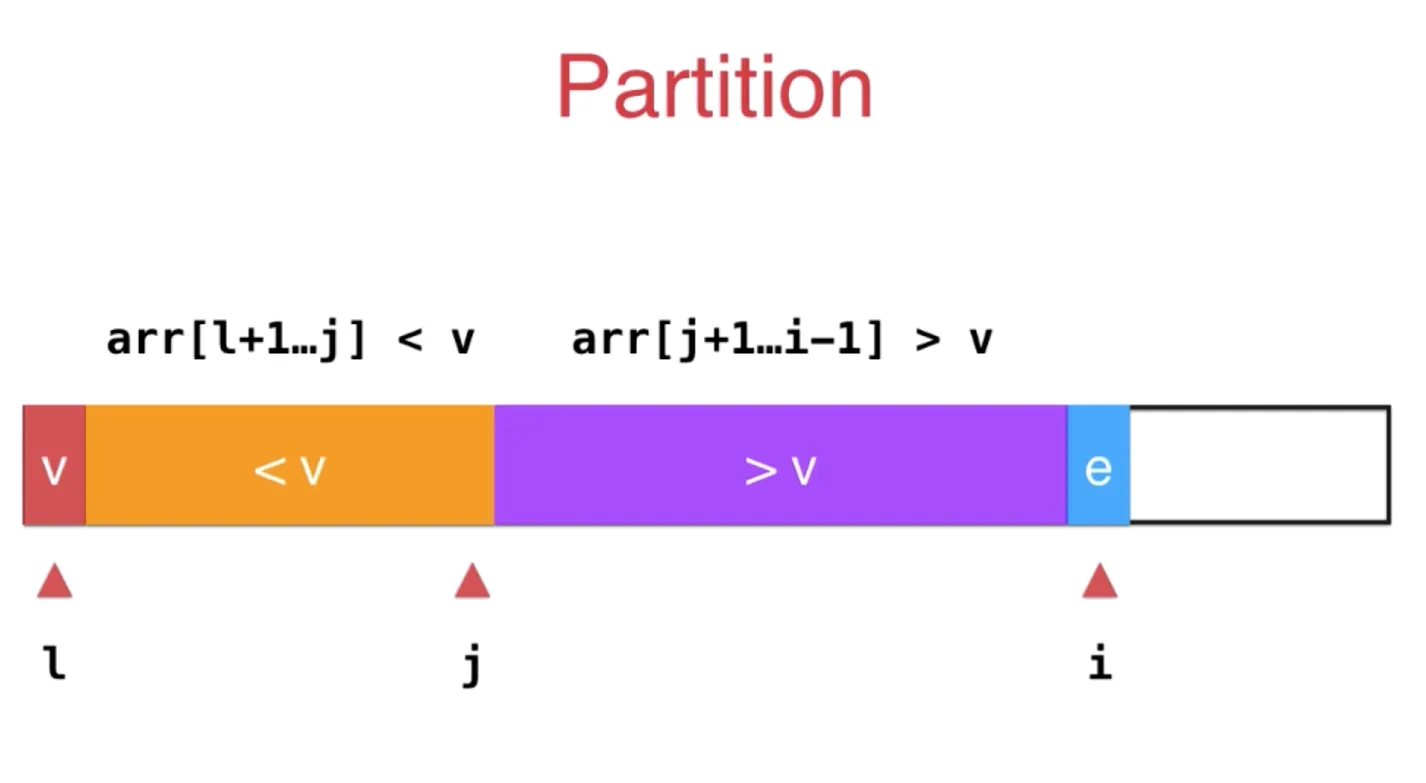
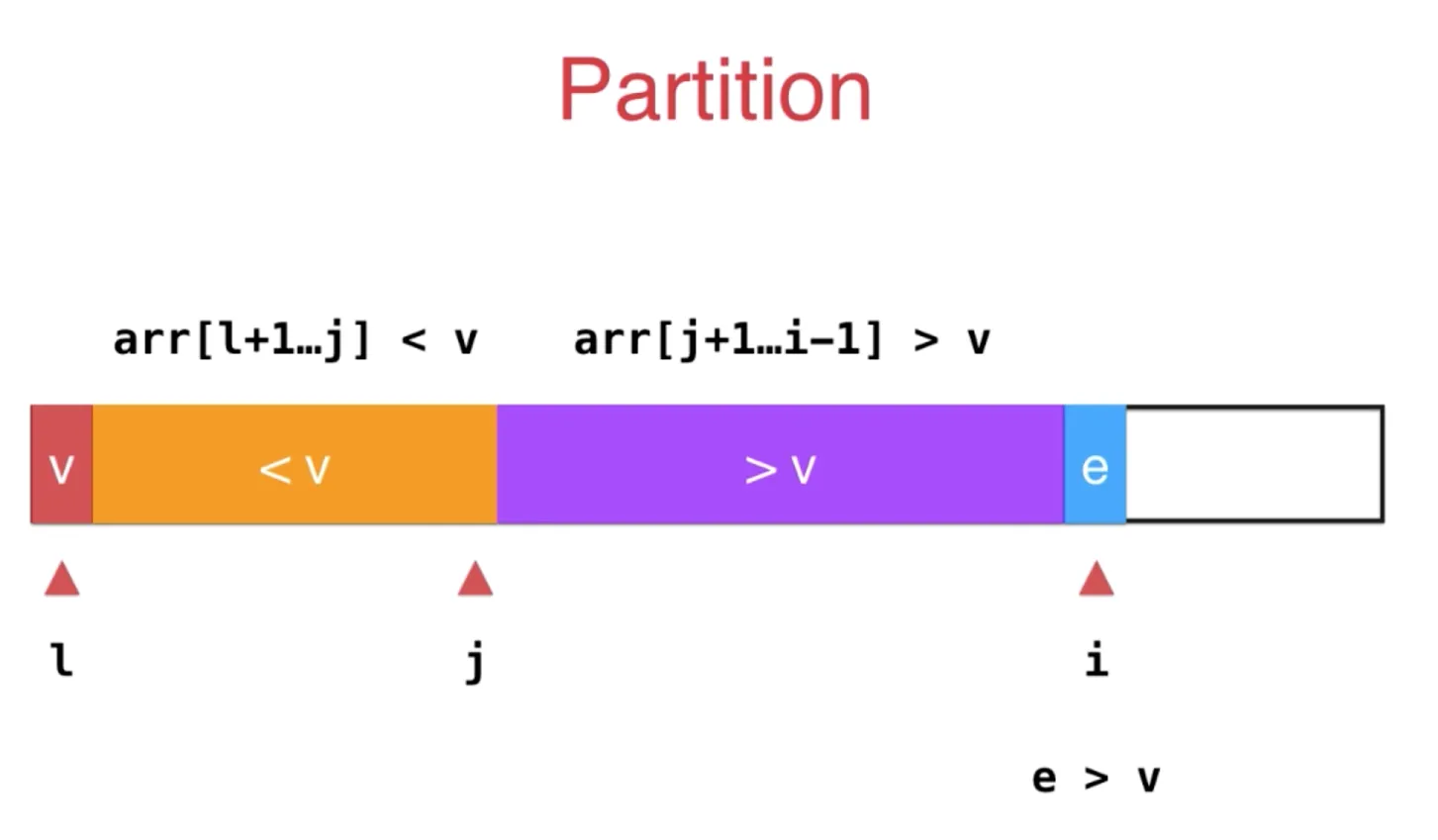
如果 i 指向的元素 e 大于 v, i++ 即可,它就处于 > v 的区间中
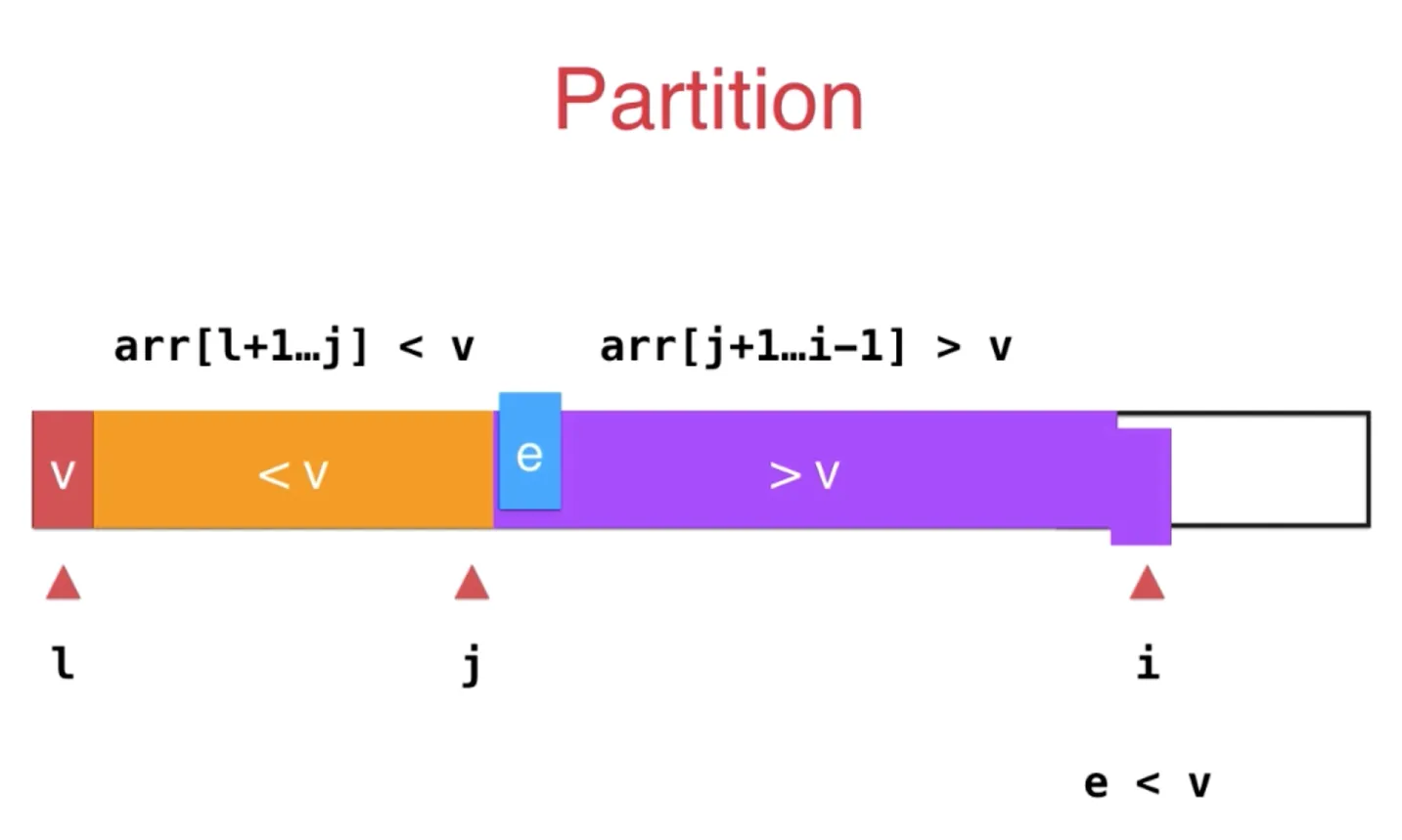
如果 e<v, 那么让 j+1 和 i 指向元素互换即可
最后,将 l, 和 j 指向元素交换即可
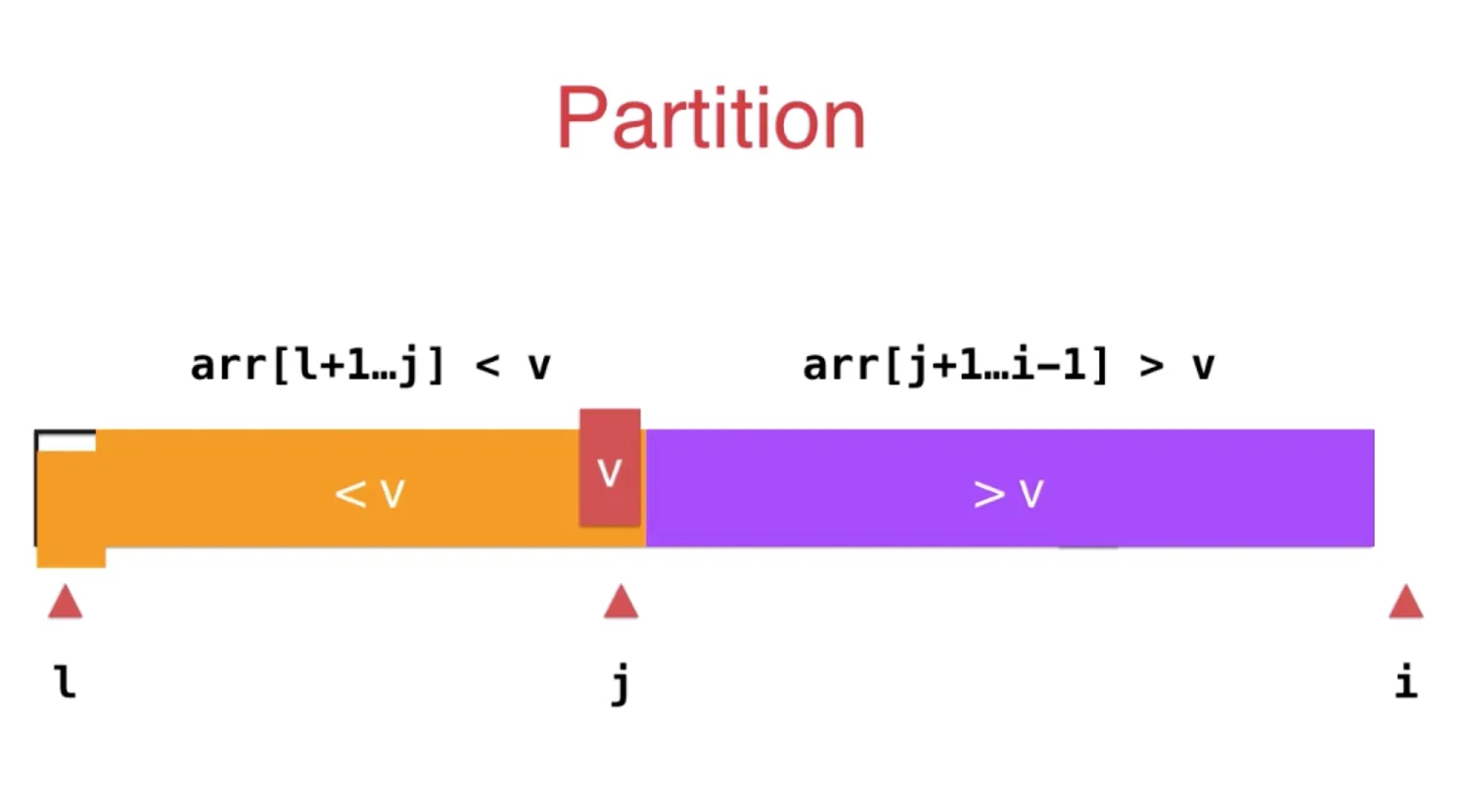
存在的问题
完全有序的情况
对于完全有序的数组,每次都会对少一个元素的有序数组进行递归,时间复杂度 O(n^2), 递归深度 O(n)
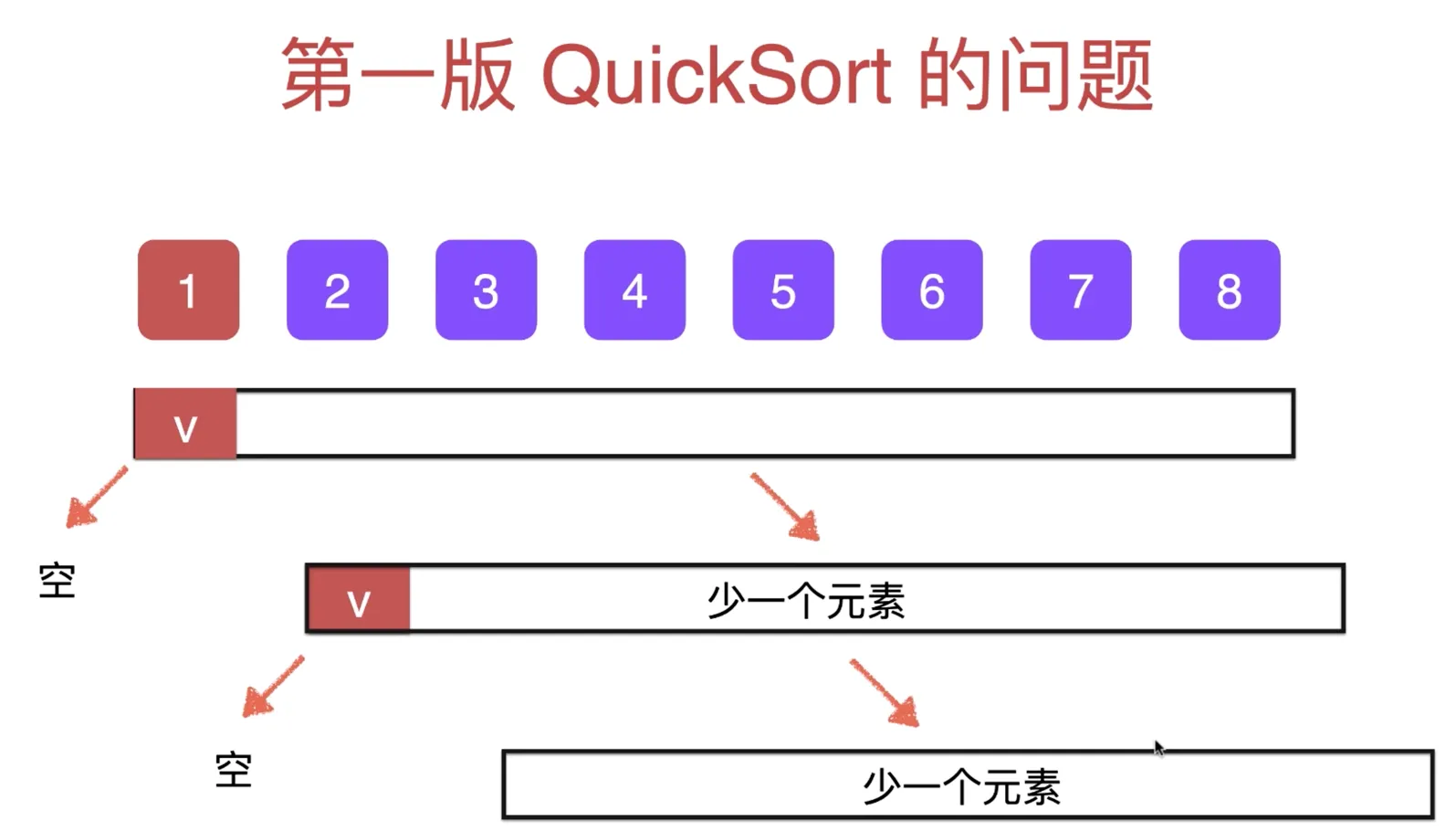
解决方案:
不使用第一个元素作为标记点,随机选择一个元素,然后和第一个元素交换即可
完全相等的情况
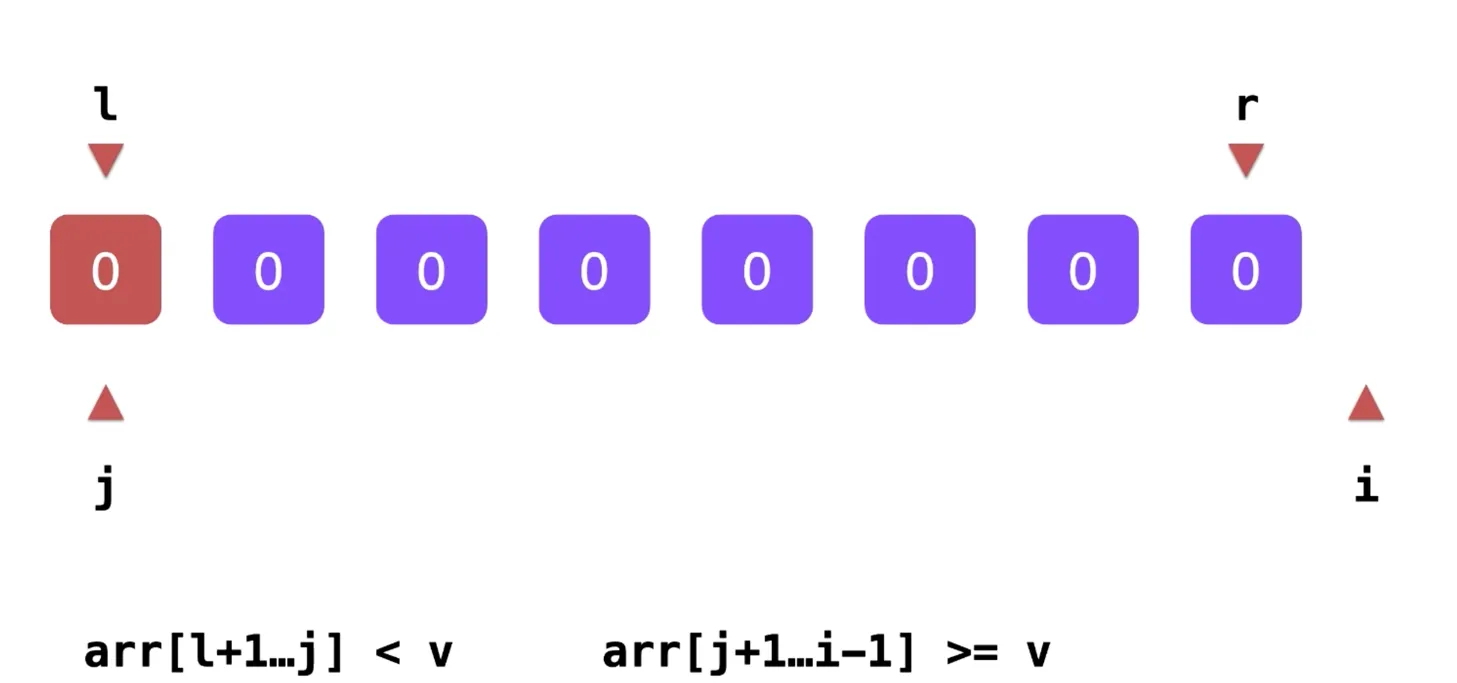
会和上面一样,时间复杂度 O(n^2) 解决方案: 双路快速排序
双路快速排序
v 为标定点,左边的元素存放小于 v 的元素,右边的元素存放大于 v 的元素
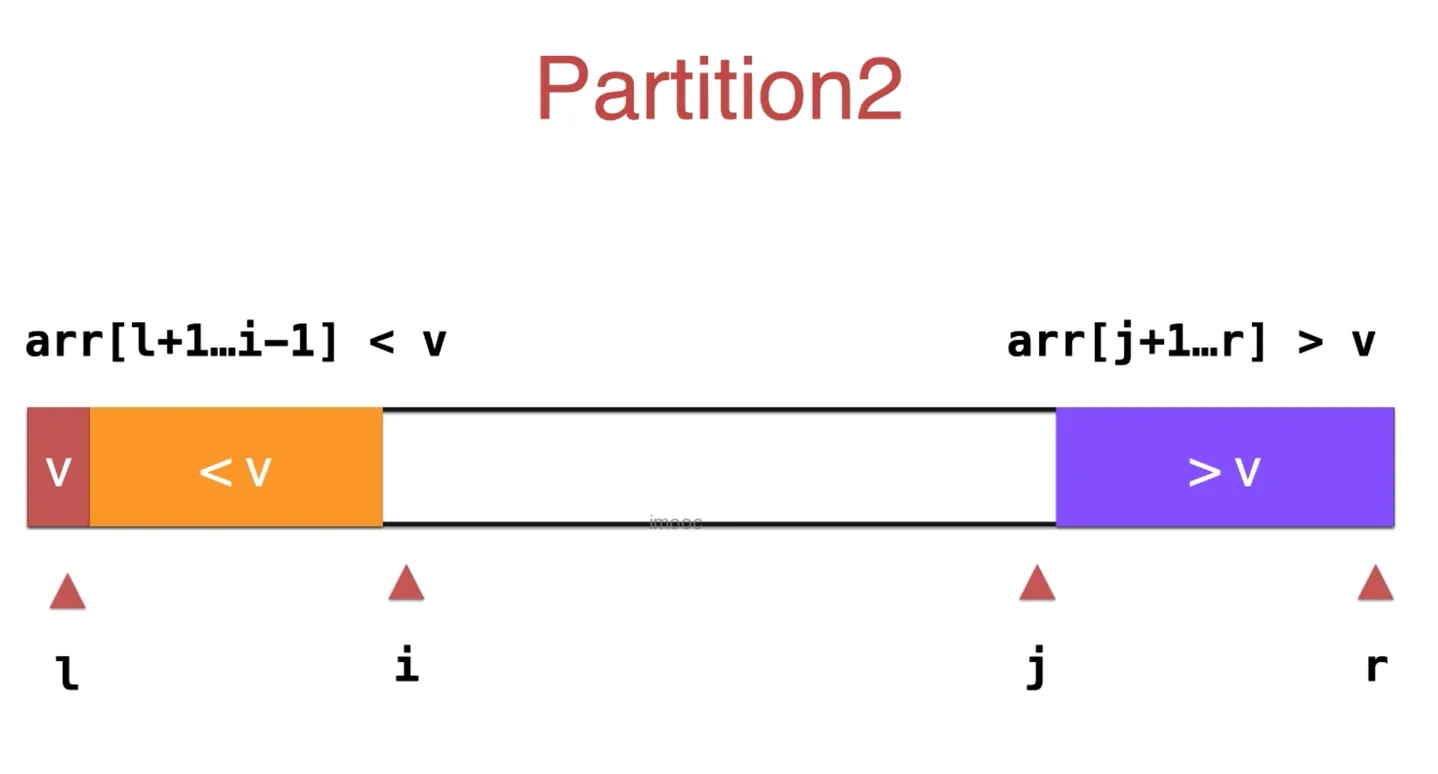
i 从 l 开始扫描,所有遇到小于等于 v 的元素,i++,直到遇到大于 v 的元素
j 从 r 开始扫描,所有遇到大等于于 v 的元素,j—,直到遇到小于 v 的元素
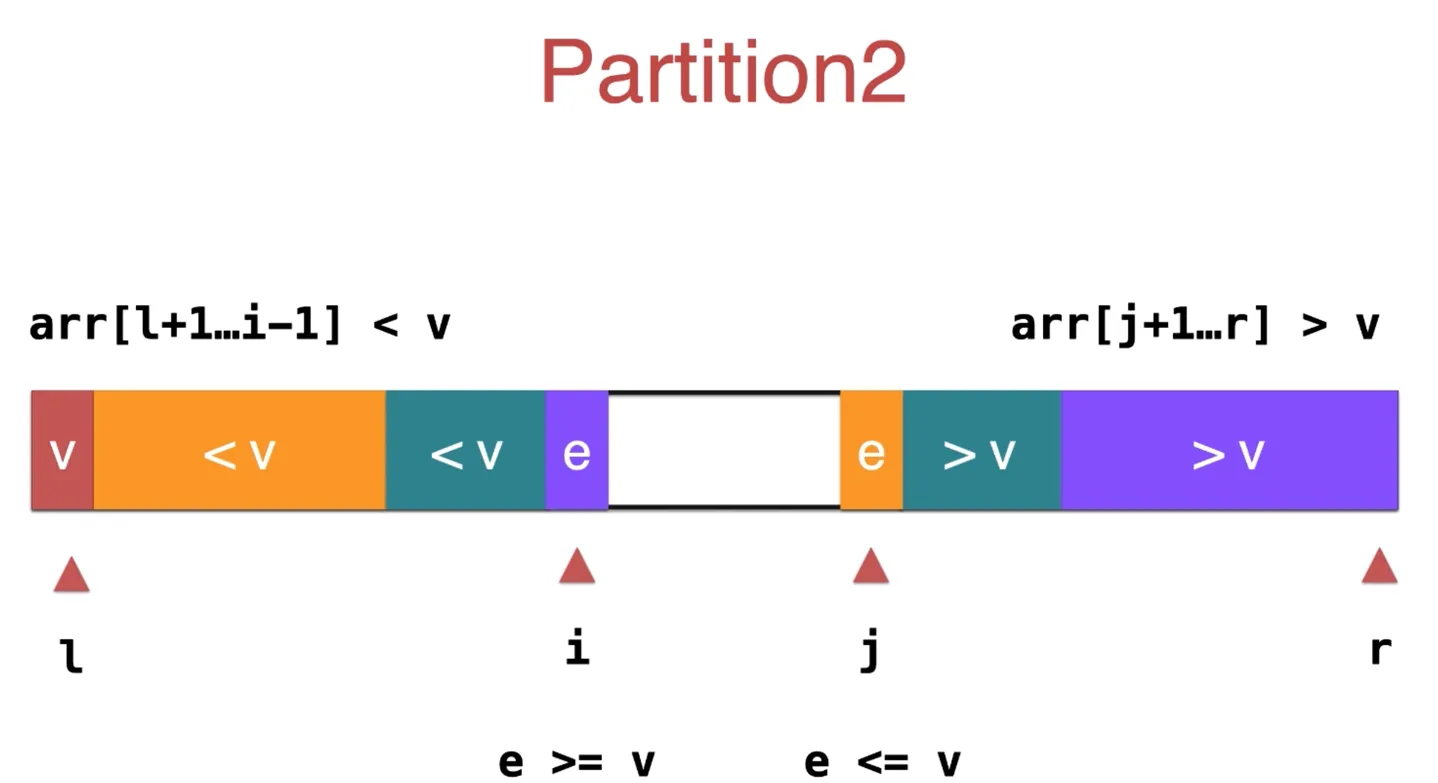
然后把这两个元素交换位置,这样,l 到 i 都是小于 v 的元素,j 到 r 都是大于 v 的元素,然后 i++, j— 继续扫描
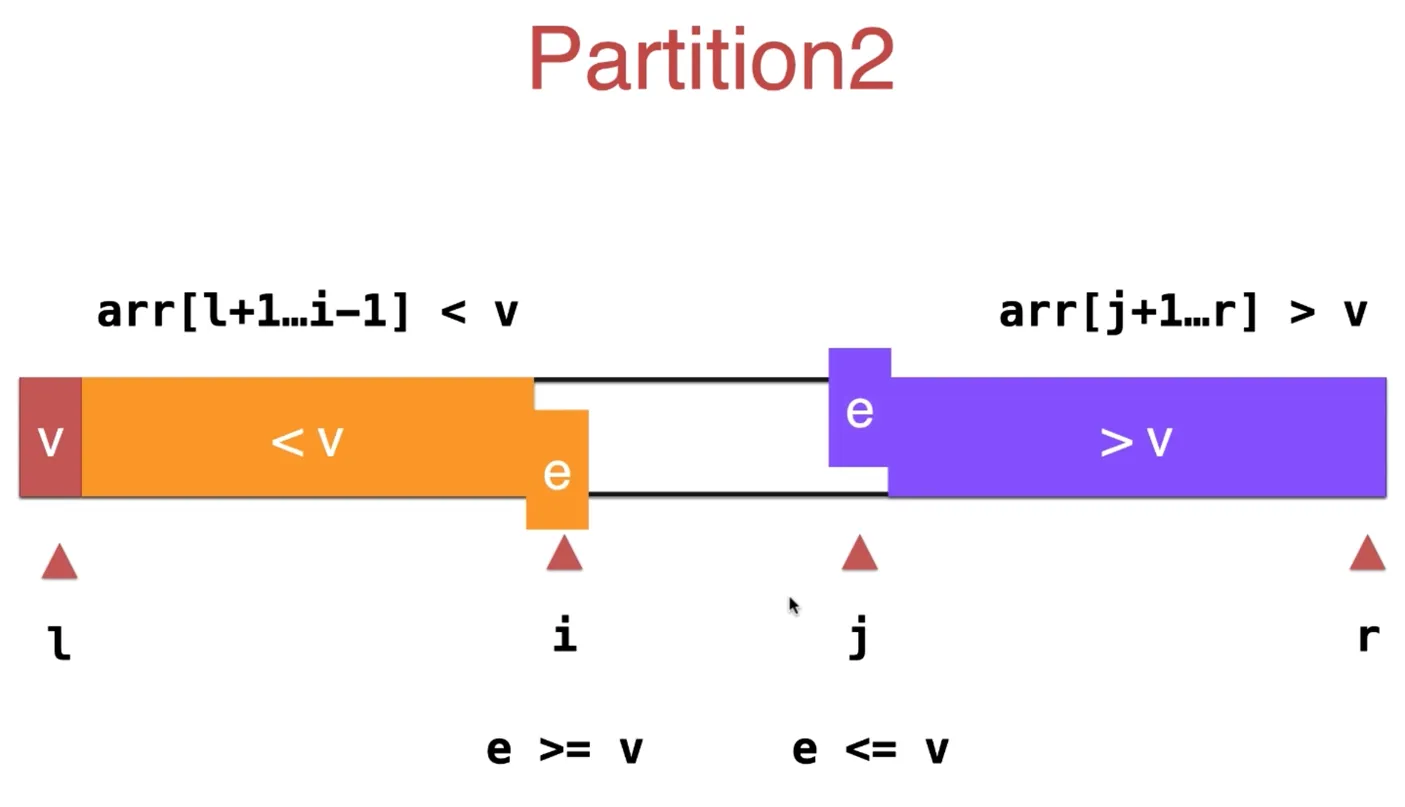
最坏情况下,时间复杂度 O(n^2),概率很小 平均情况下,时间复杂度 O(nlogn)
三路快速排序
对于元素都相同的情况,可以不用再次排序 三路排序在排序过程中,把数组划分为了三部分,小于 v,等于 v,大于 v
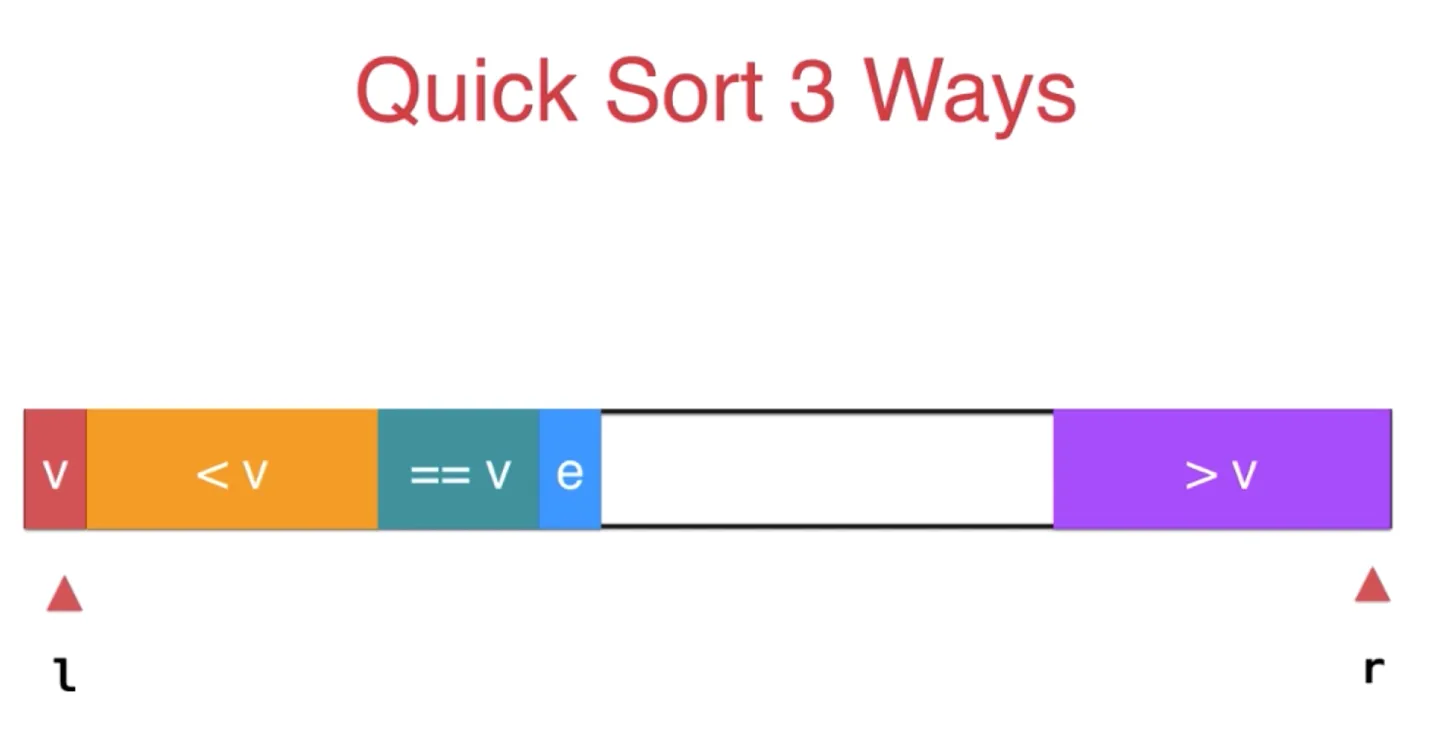
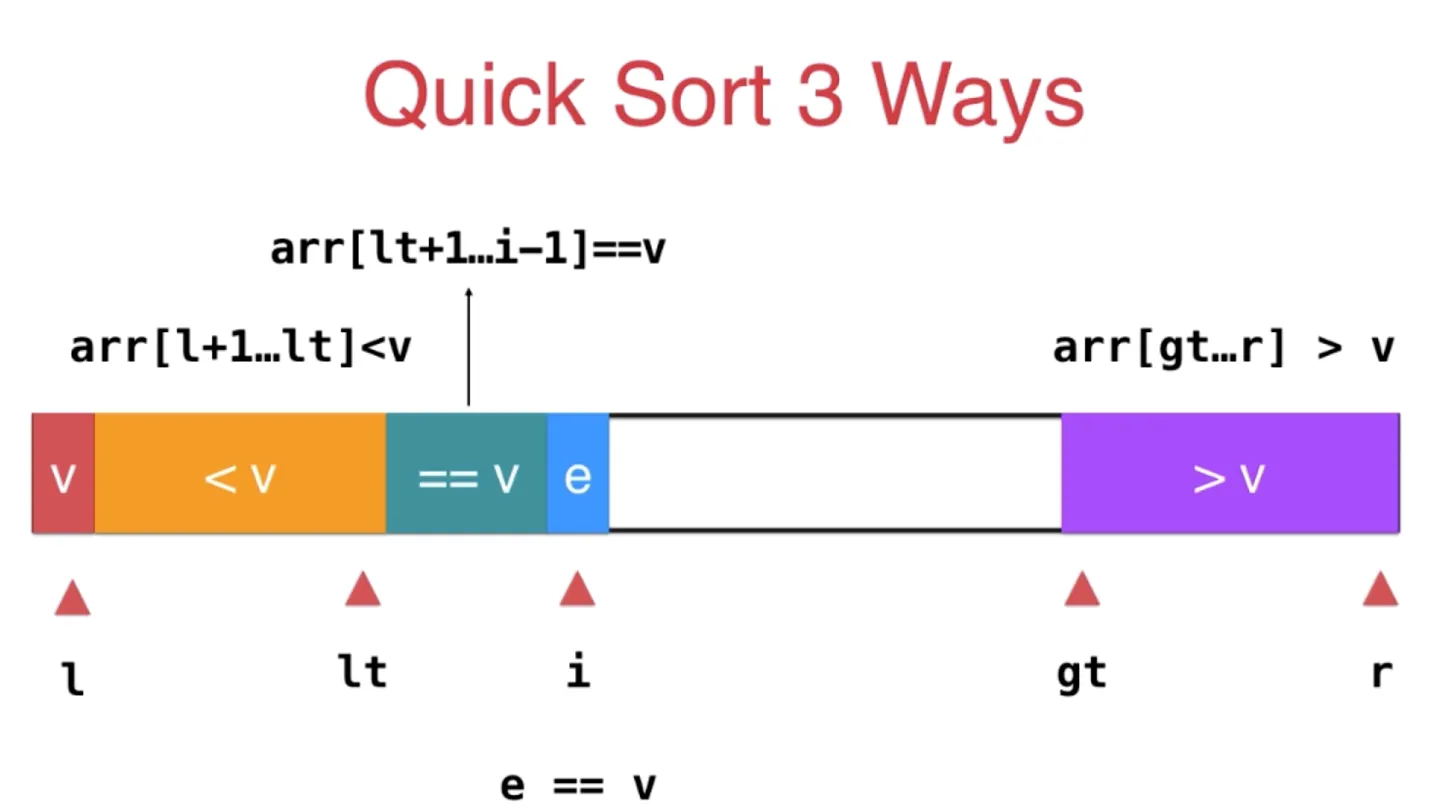 对于元素 e, 如果 等于 v, 那么直接划入等于 v 的部分,i++
如果 e < v, 那么和等于 v 的第一个元素交换位置,i++, lt++
如果 e > v, 那么和大于 v 前的第一个元素交换位置,gt—
终止条件,i >= gt
最后,把 l 和 lt 位置的元素交换位置
对于元素 e, 如果 等于 v, 那么直接划入等于 v 的部分,i++
如果 e < v, 那么和等于 v 的第一个元素交换位置,i++, lt++
如果 e > v, 那么和大于 v 前的第一个元素交换位置,gt—
终止条件,i >= gt
最后,把 l 和 lt 位置的元素交换位置

速度对比
Random Array:
MergeSort, n = 1000000 : 0.429069 s
QuickSort, n = 1000000 : 0.257638 s
QuickSort2Ways, n = 1000000 : 0.209404 s
QuickSort3Ways, n = 1000000 : 0.400175 s
Ordered Array:
MergeSort, n = 1000000 : 0.003160 s
QuickSort, n = 1000000 : 0.189545 s
QuickSort2Ways, n = 1000000 : 0.050844 s
QuickSort3Ways, n = 1000000 : 0.382524 s
Save value Array:
MergeSort, n = 1000000 : 0.002958 s
QuickSort2Ways, n = 1000000 : 0.148120 s
QuickSort3Ways, n = 1000000 : 0.001708 s使用三路快速排序解决
Select K 问题
给出一个无序数组,找出数组的第,k 小的元素

经过一轮 partition 后,我们可以获得,小于标定点的元素,和大于标定点的元素,
标定点此时在数组中的位置是确定的
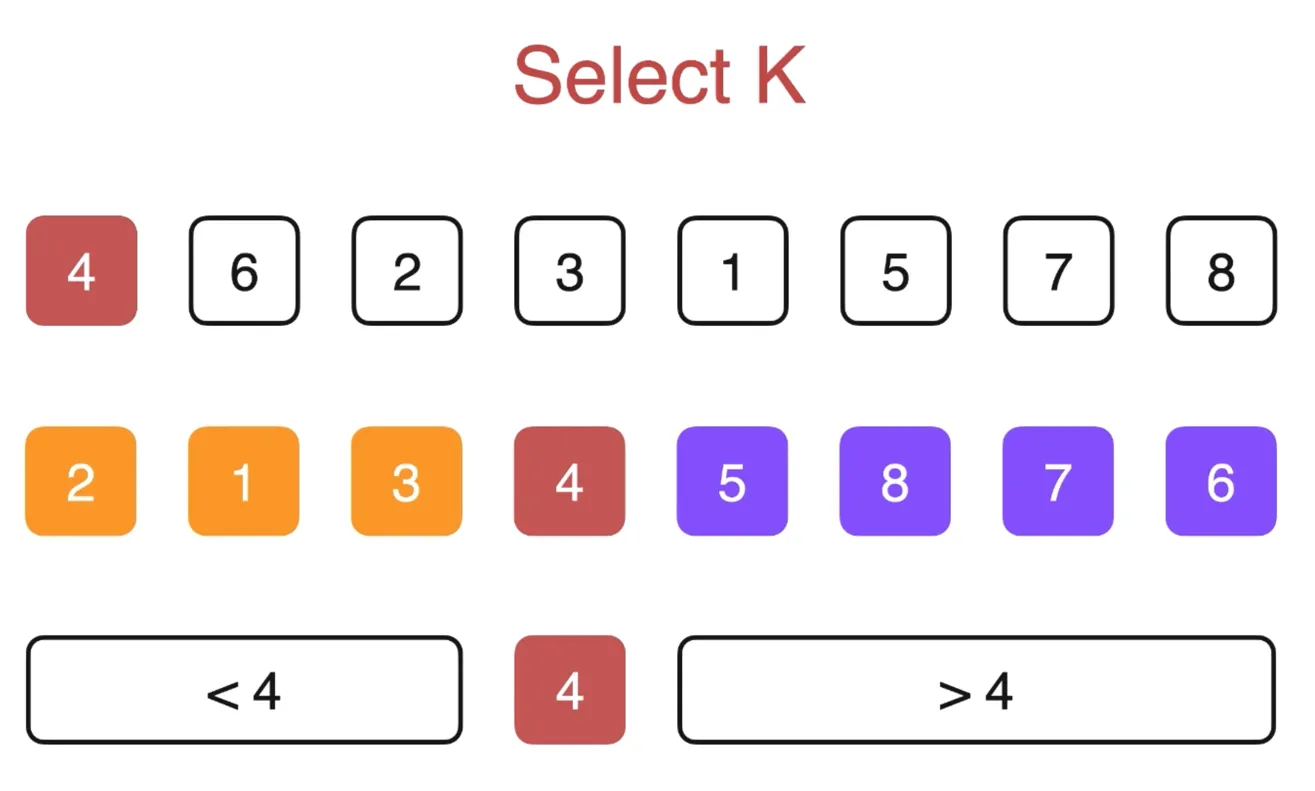
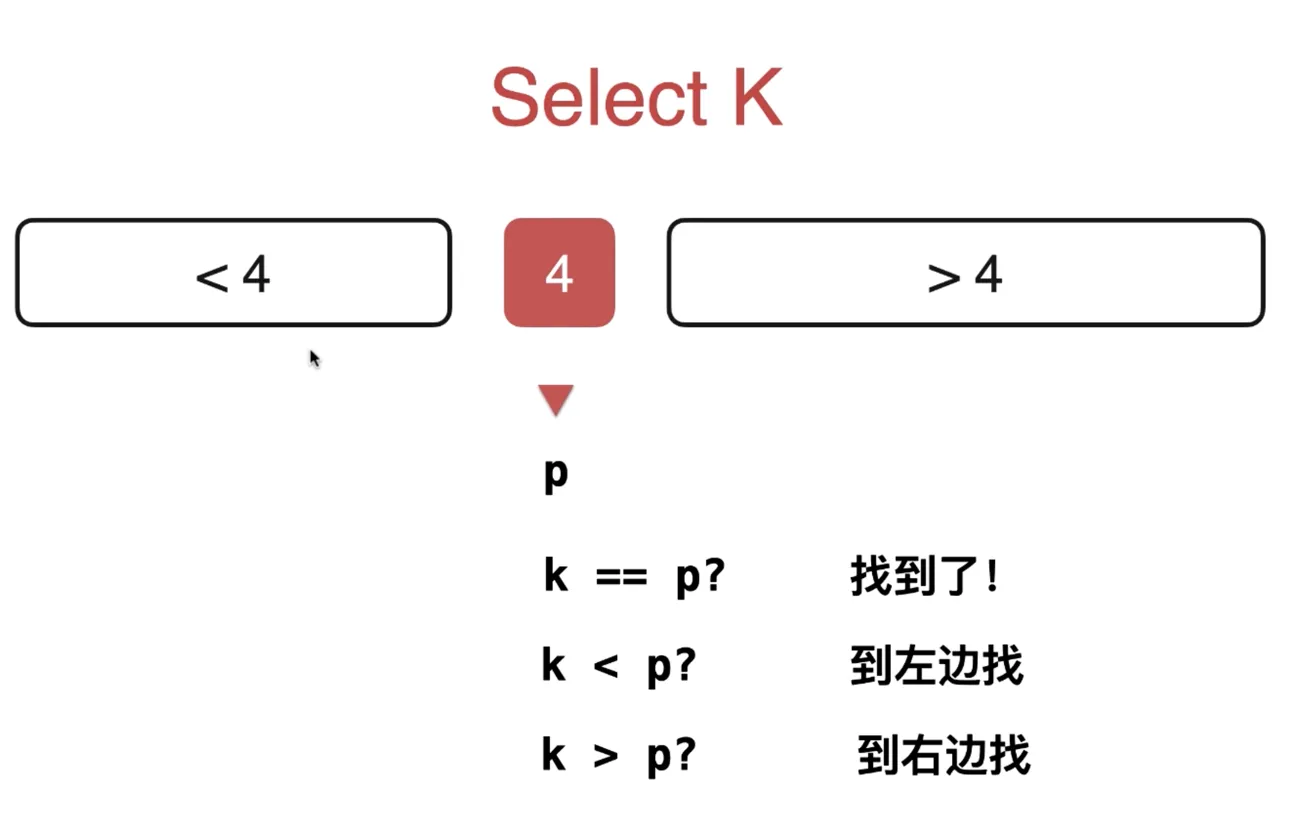
类似的题目,数组中第 k 个最大的元素 最小的k个数
二分查找
算法复杂度O(logn)
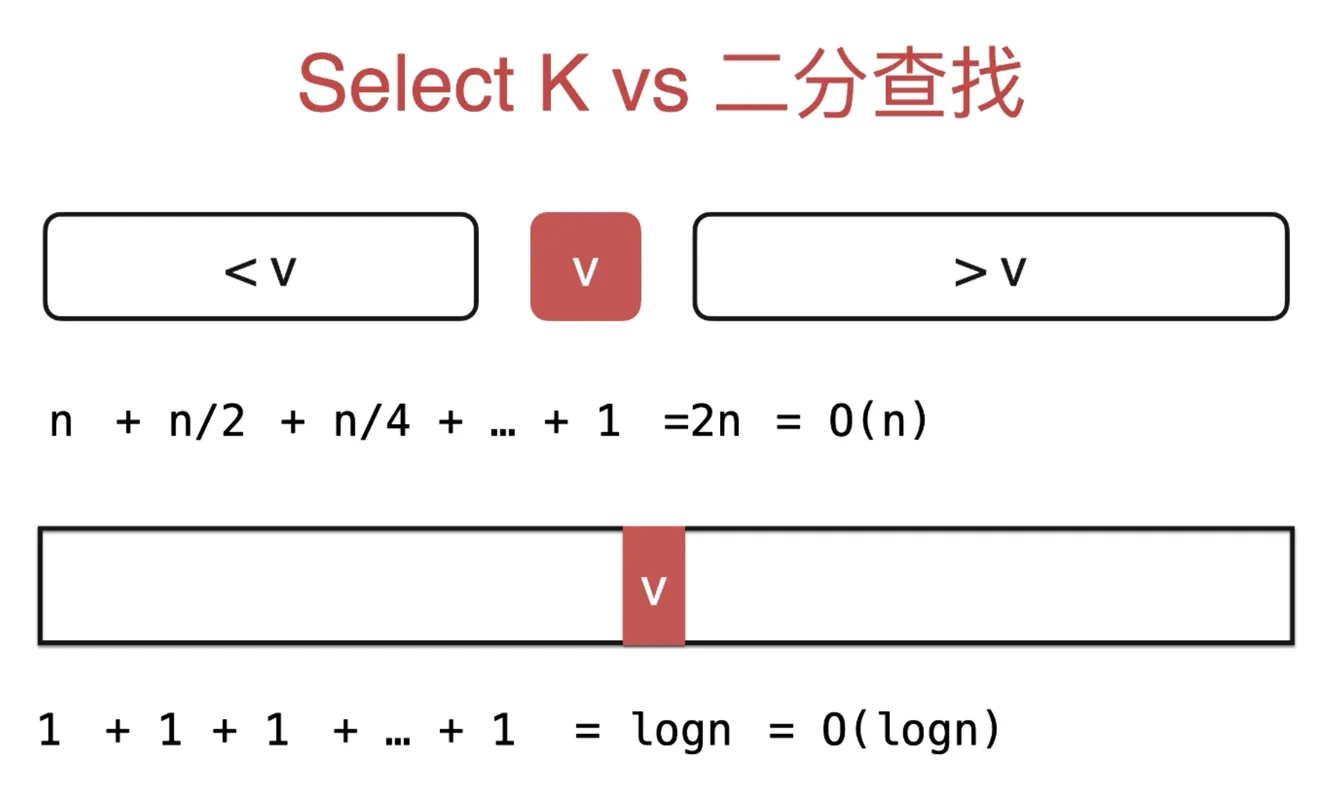
二分查找法变种:upper
查找大于 target 的最小值
二分查找法变种:ceil

二分查找法变种:lower_ceil

二分查找法变种:lower
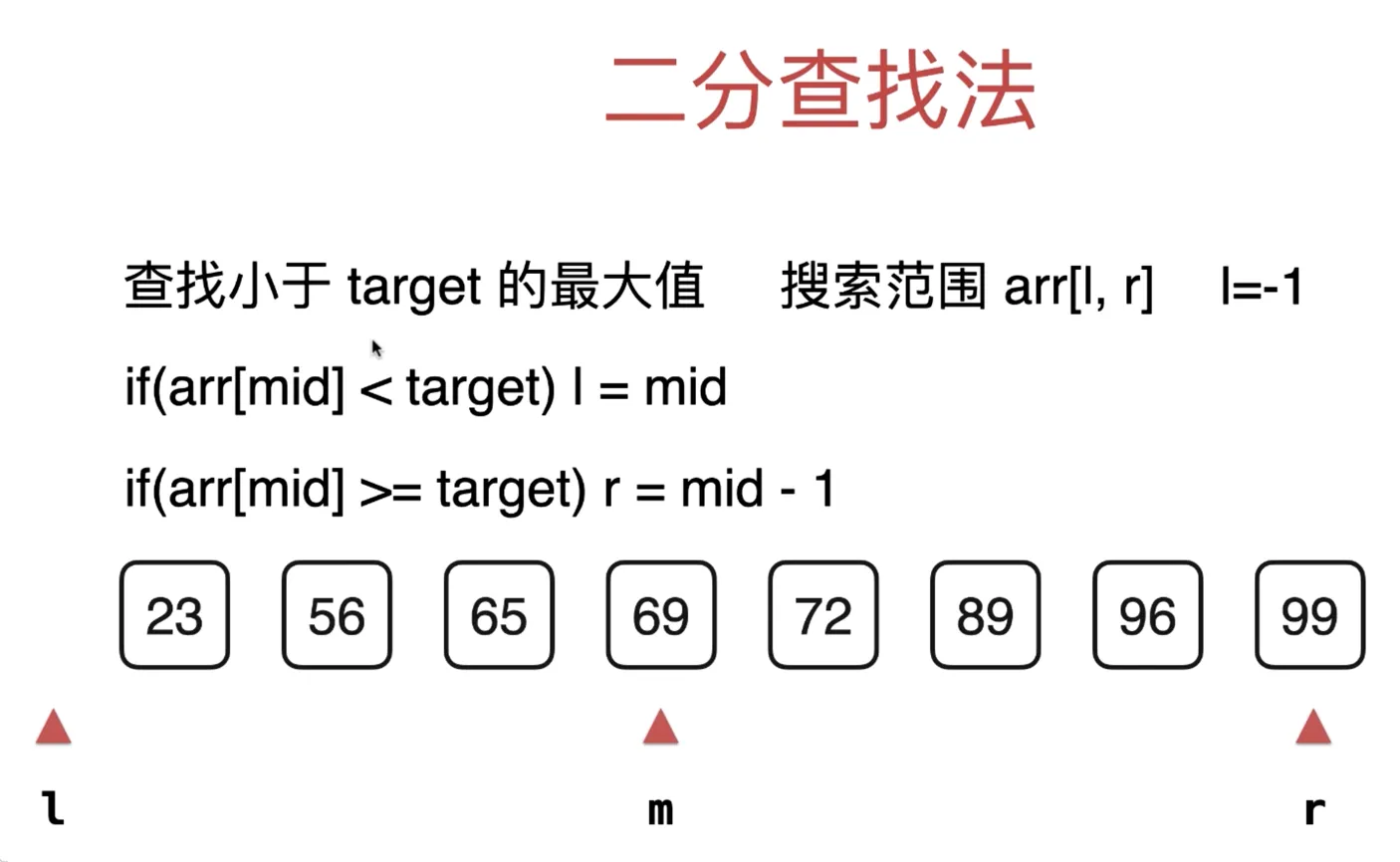
二分查找法变种:lower_floor
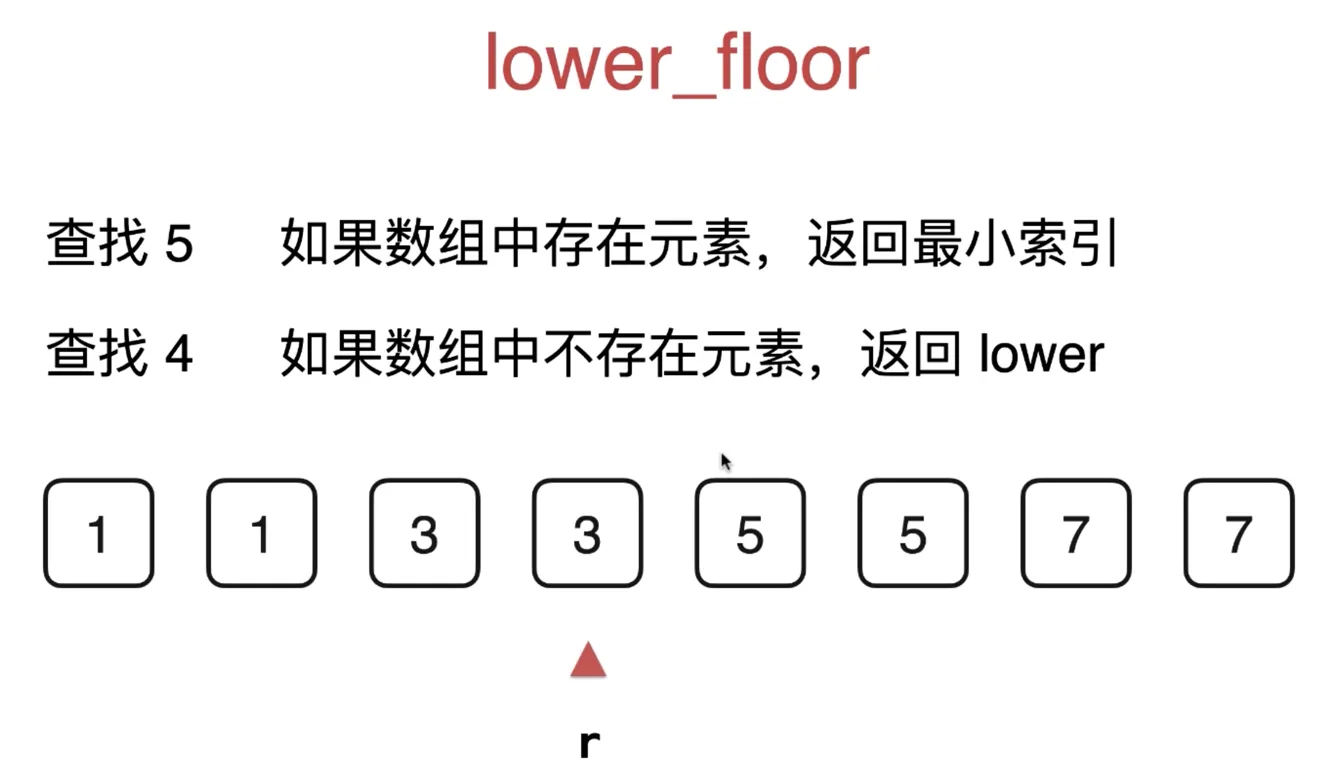
二分查找法变种:upper_floor
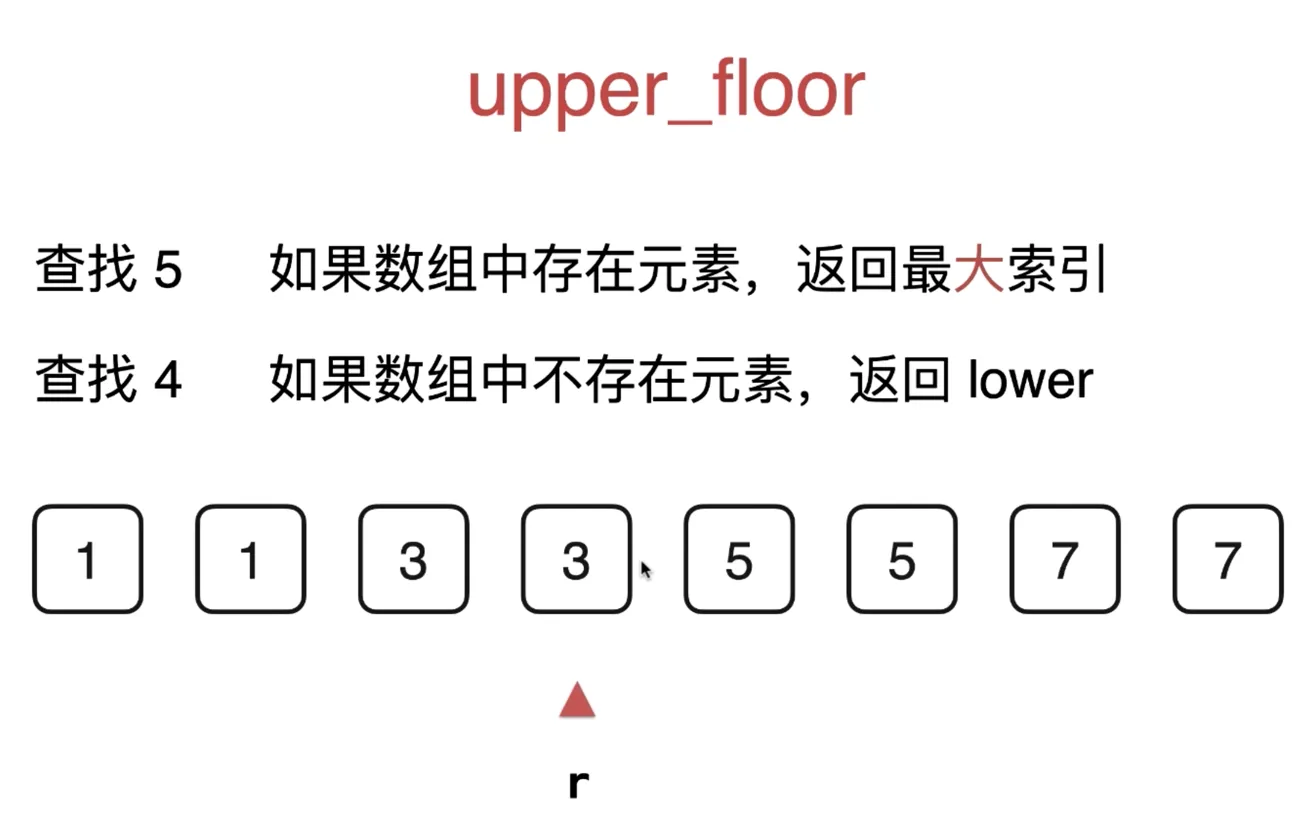
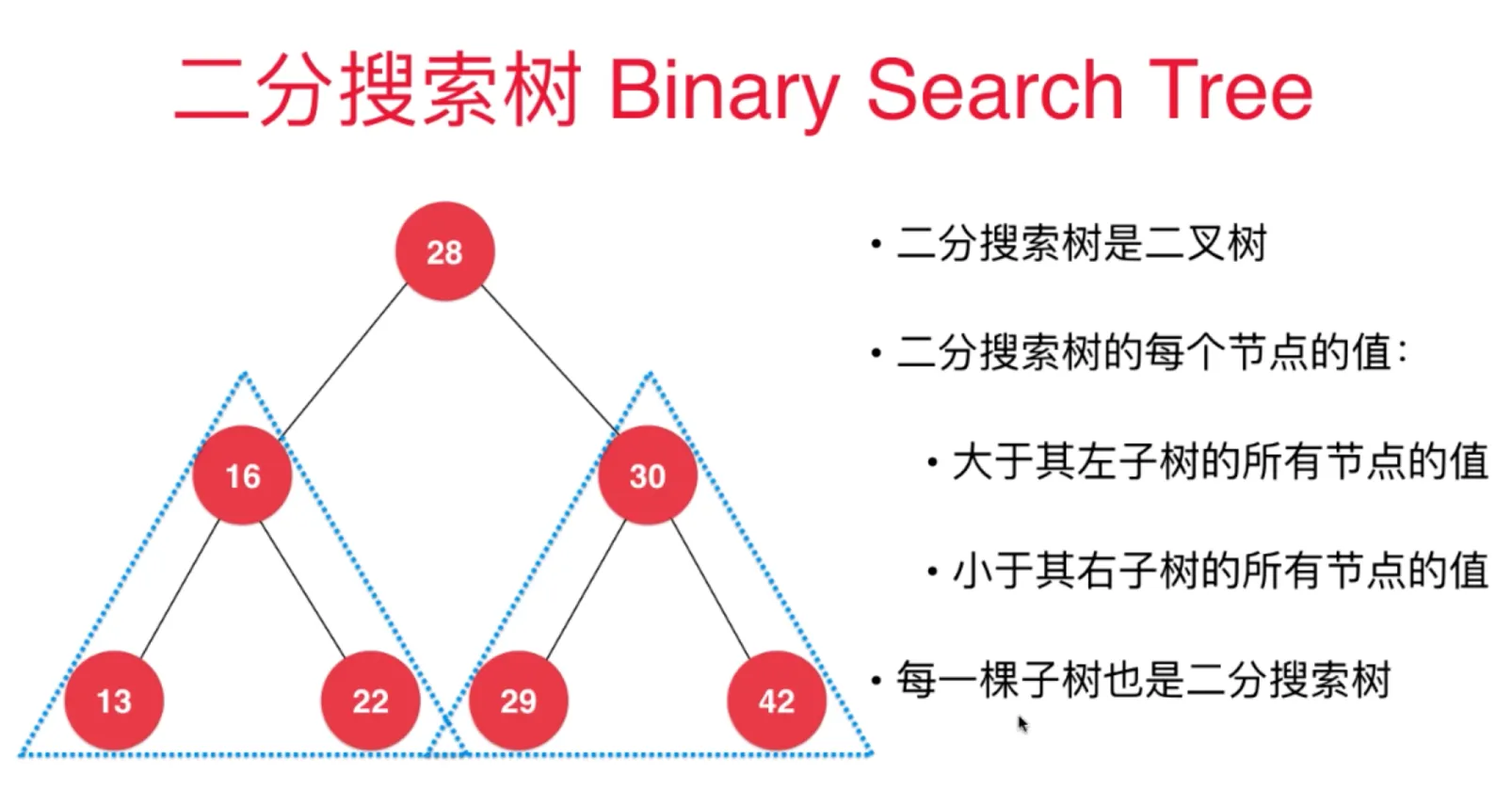
二分搜索树
定义:
- 二分搜索树是二叉树
- 二分搜索树的每个节点的值:
- 大于起左子树所有节点的值
- 小于起右子树所有节点的值
- 每一颗子树也是二分搜索树
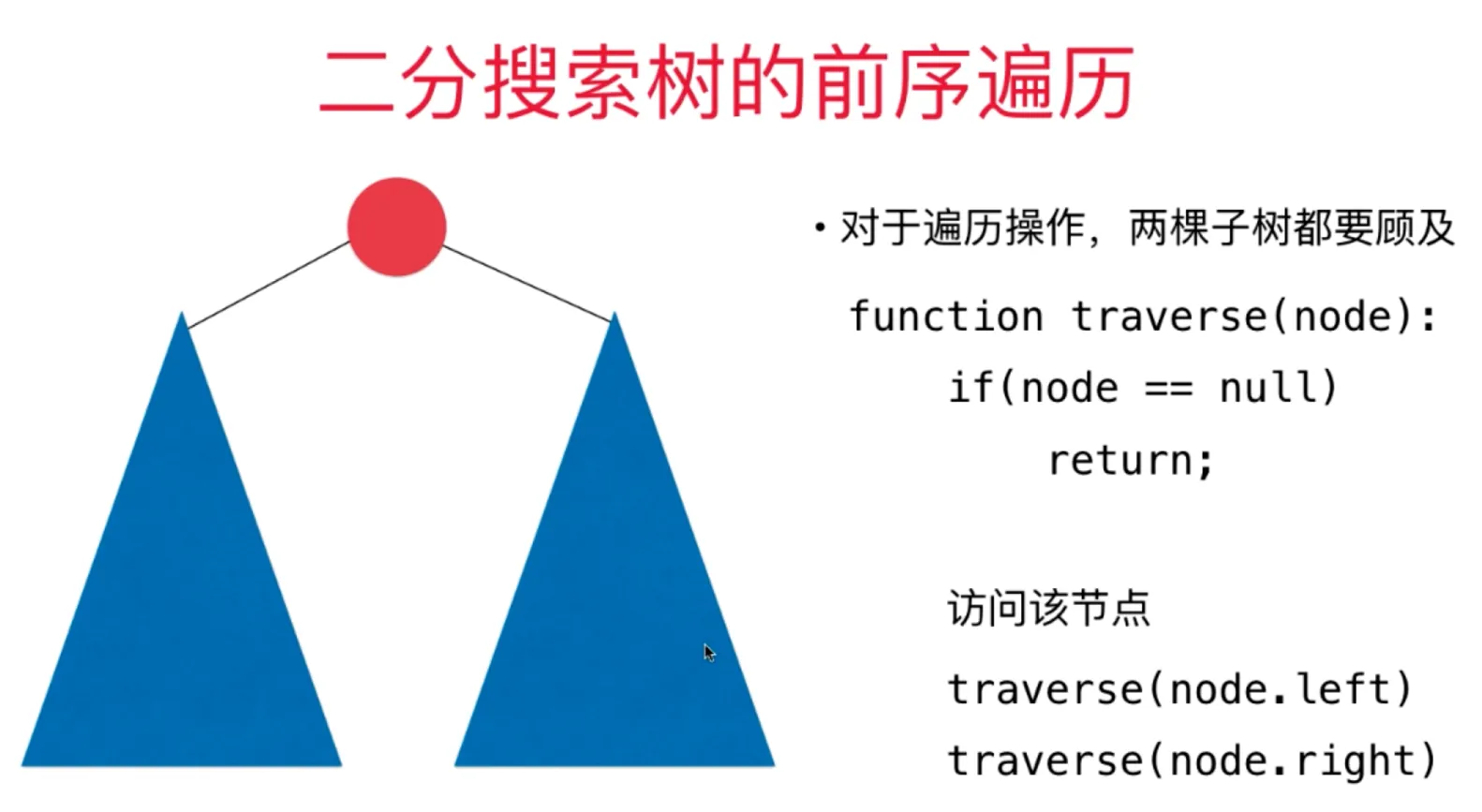
二分搜索树遍历
前序遍历
访问的节点在左右子树的前面
中序遍历: 先左,后节点,最后右边, 这个输出结果就是从小到大排序结果
后序遍历 应用:为二分搜索树释放内存
前序遍历的非递归写法:
先把要访问的节点压入栈,然后弹出访问其,然后分别压入右左子节点,继续弹出访问并压入右左子节点
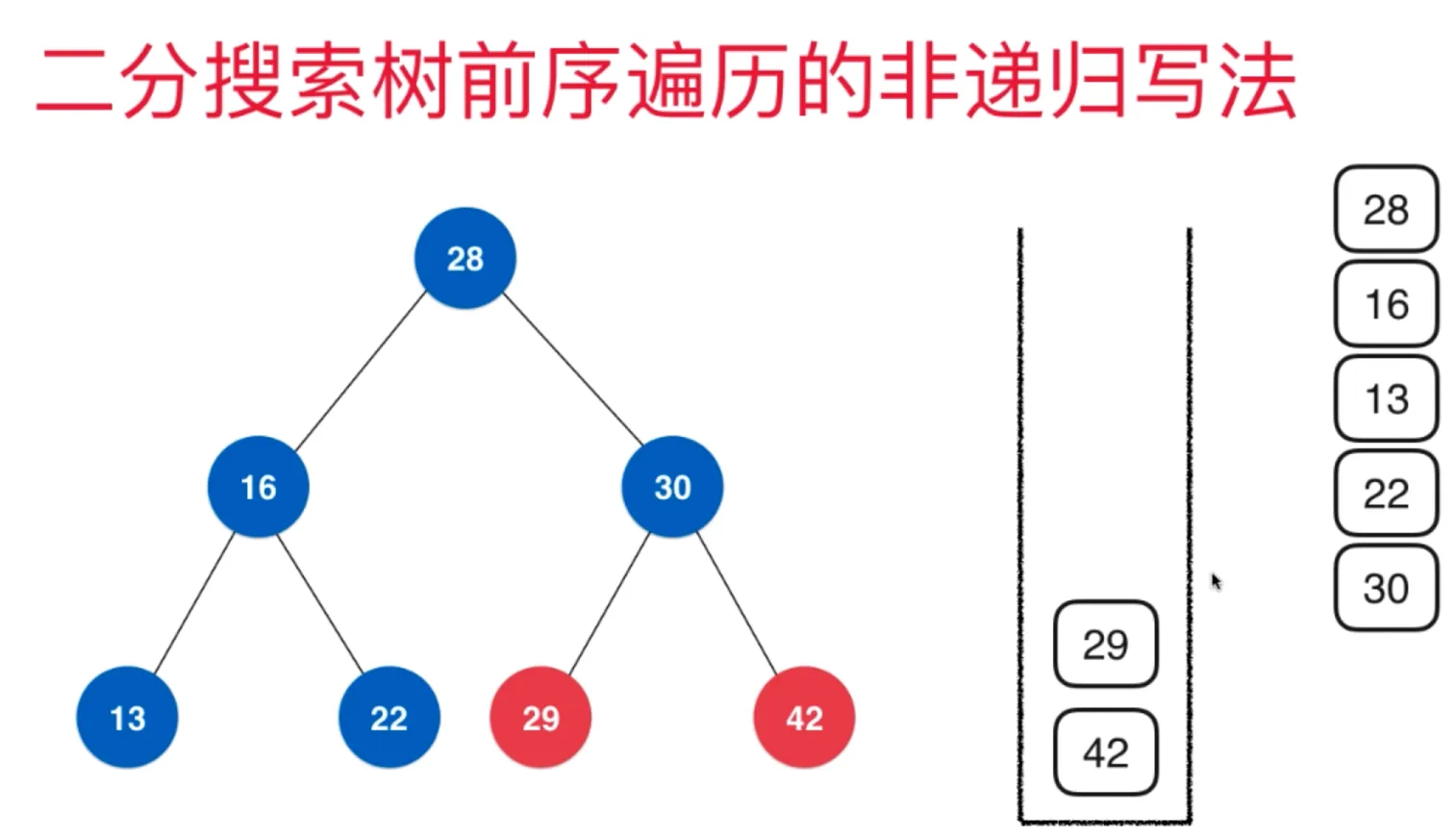
二分搜索树的层序遍历
一个队列,先入队中间节点,弹出,然后分别入队其左右节点,继续弹出后入队其左右节点
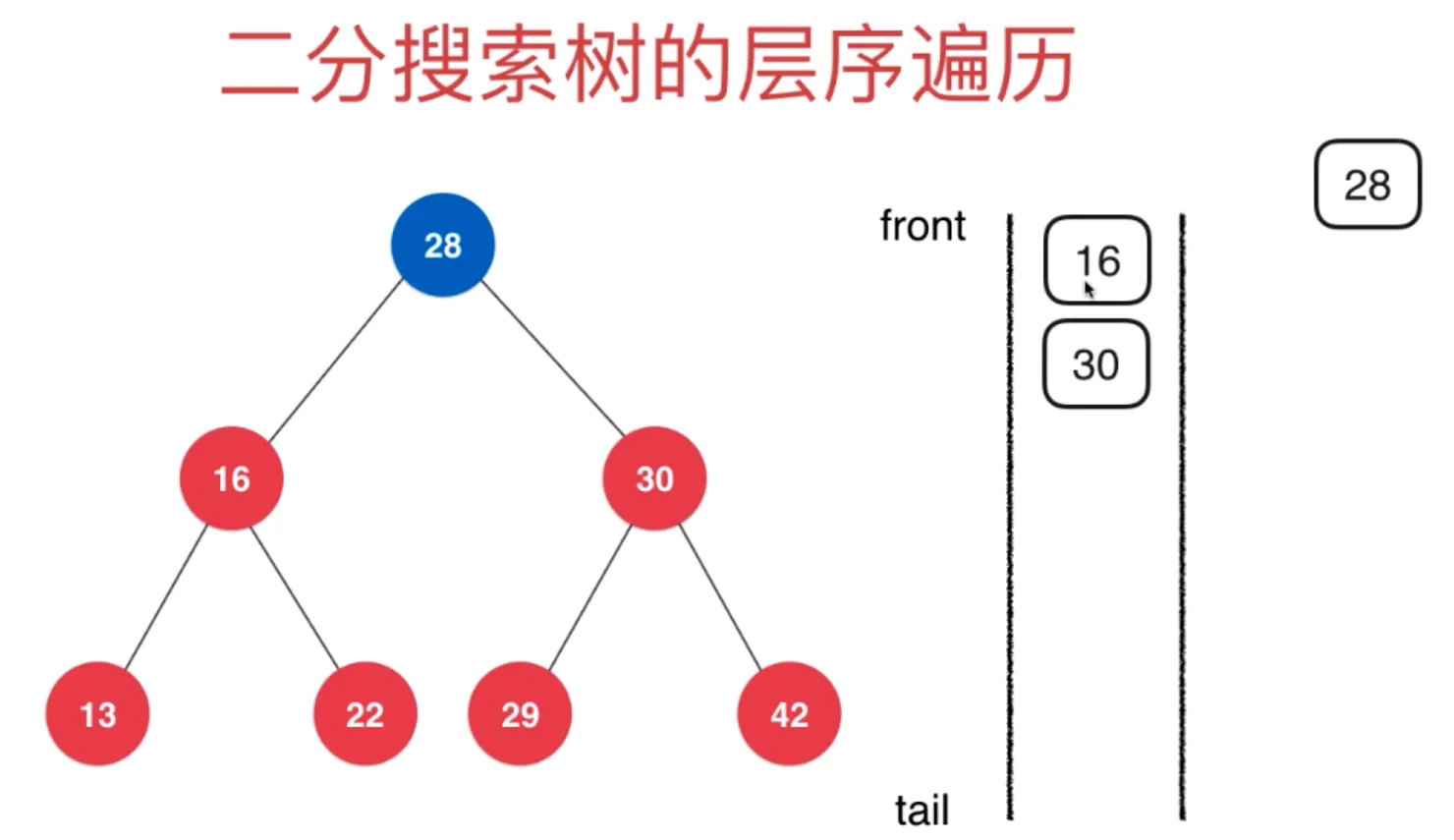
即广度优先遍历,优点
- 更快的找到问题的解
- 常用于算法设计中-最短路径
- 图中的深度优先遍历和广度优先遍历
二分搜索树的删除任意节点
如果待删除节点左子树为空,那么它的上一个节点指向它的右子树即可 如果待删除节点右子树为空,那么它的上一个节点指向它的左子树即可
如果待删除节点 d 左右子节点都在,遵循如下方法:
- 找到比待删除节点大的最小节点,即待删除节点右子树的最小节点 s = min(d->right)
- s 是 d 的后继
- s->right = delMin(d.right)
- s->left = d->left
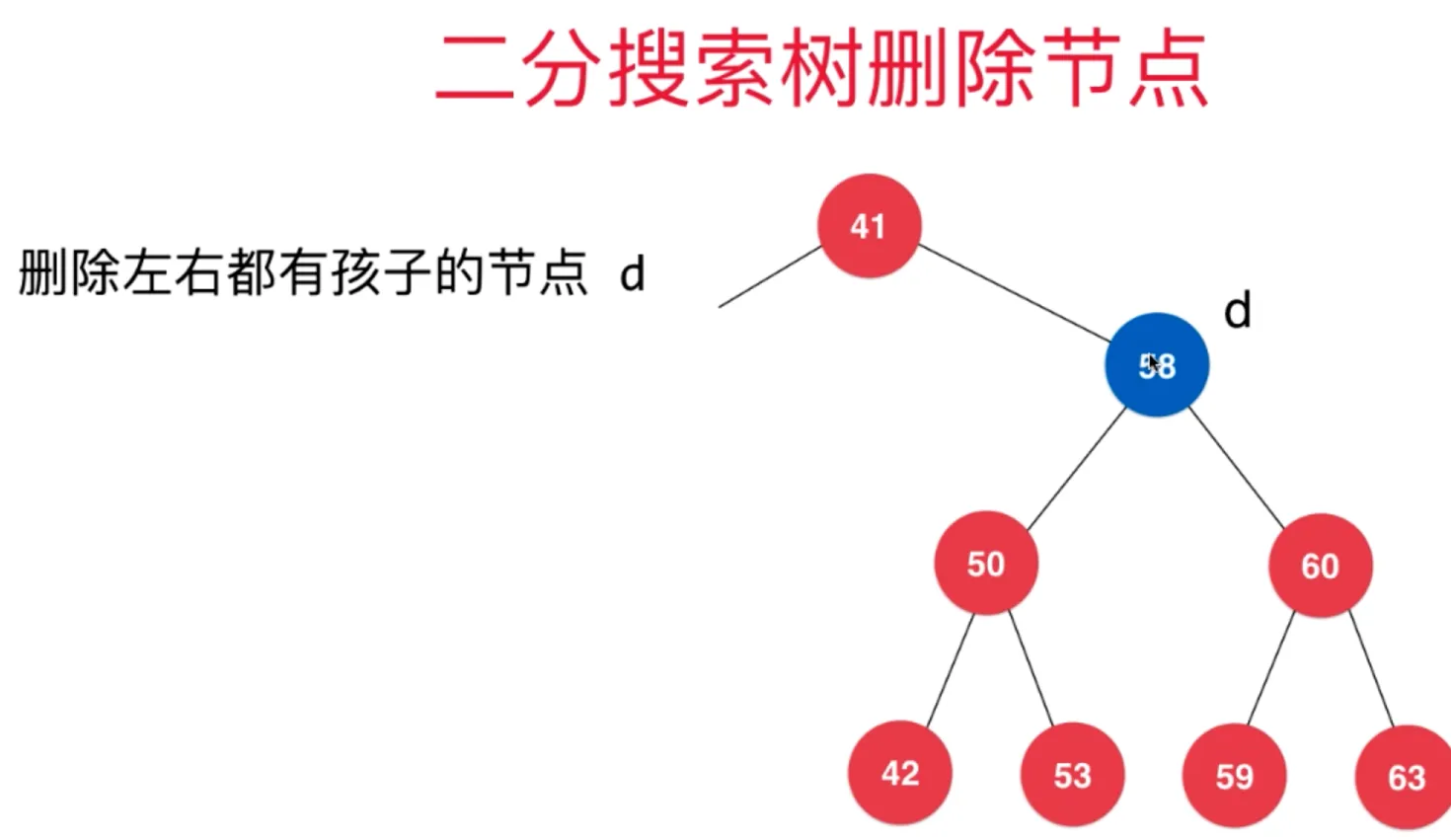
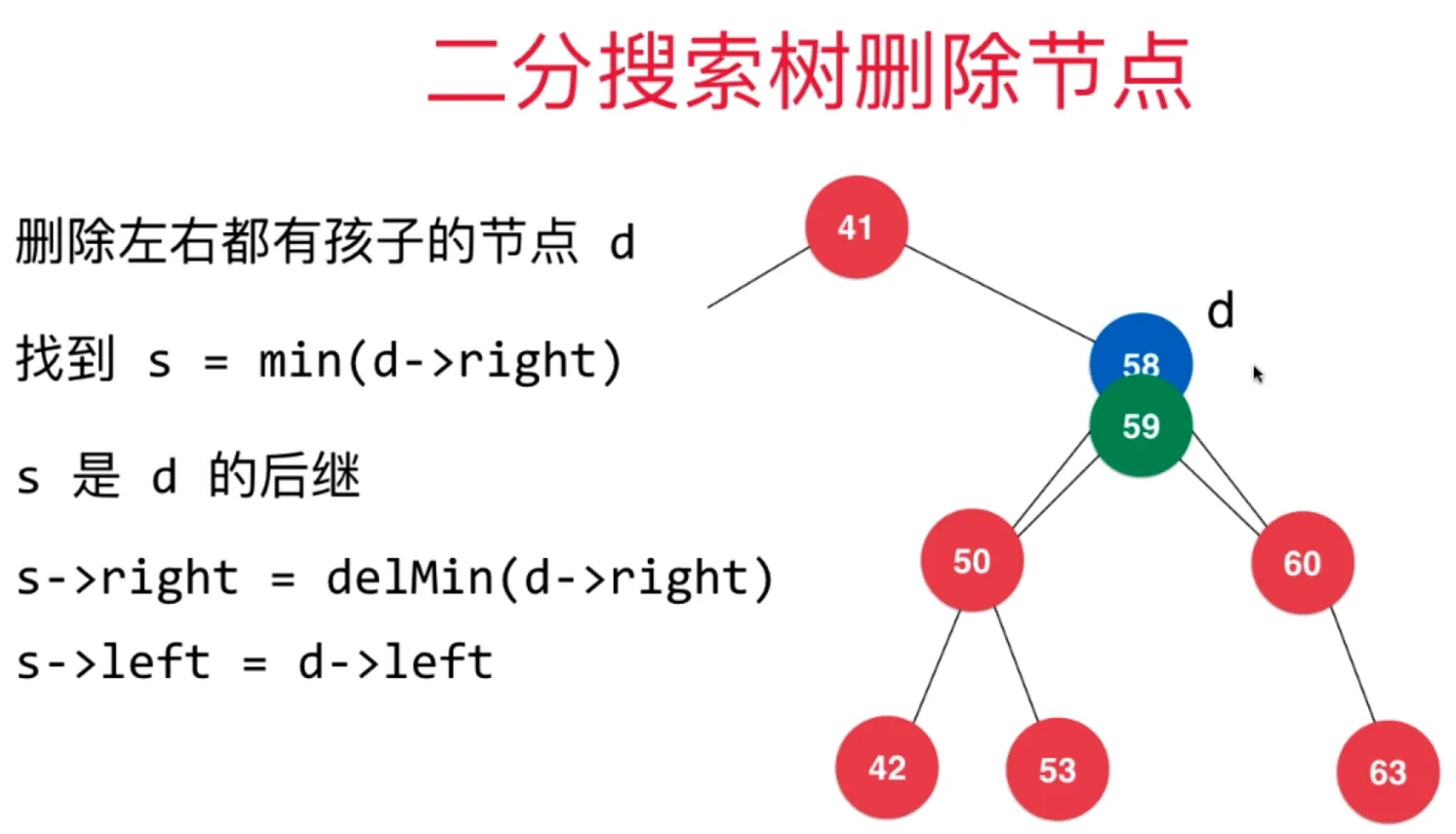
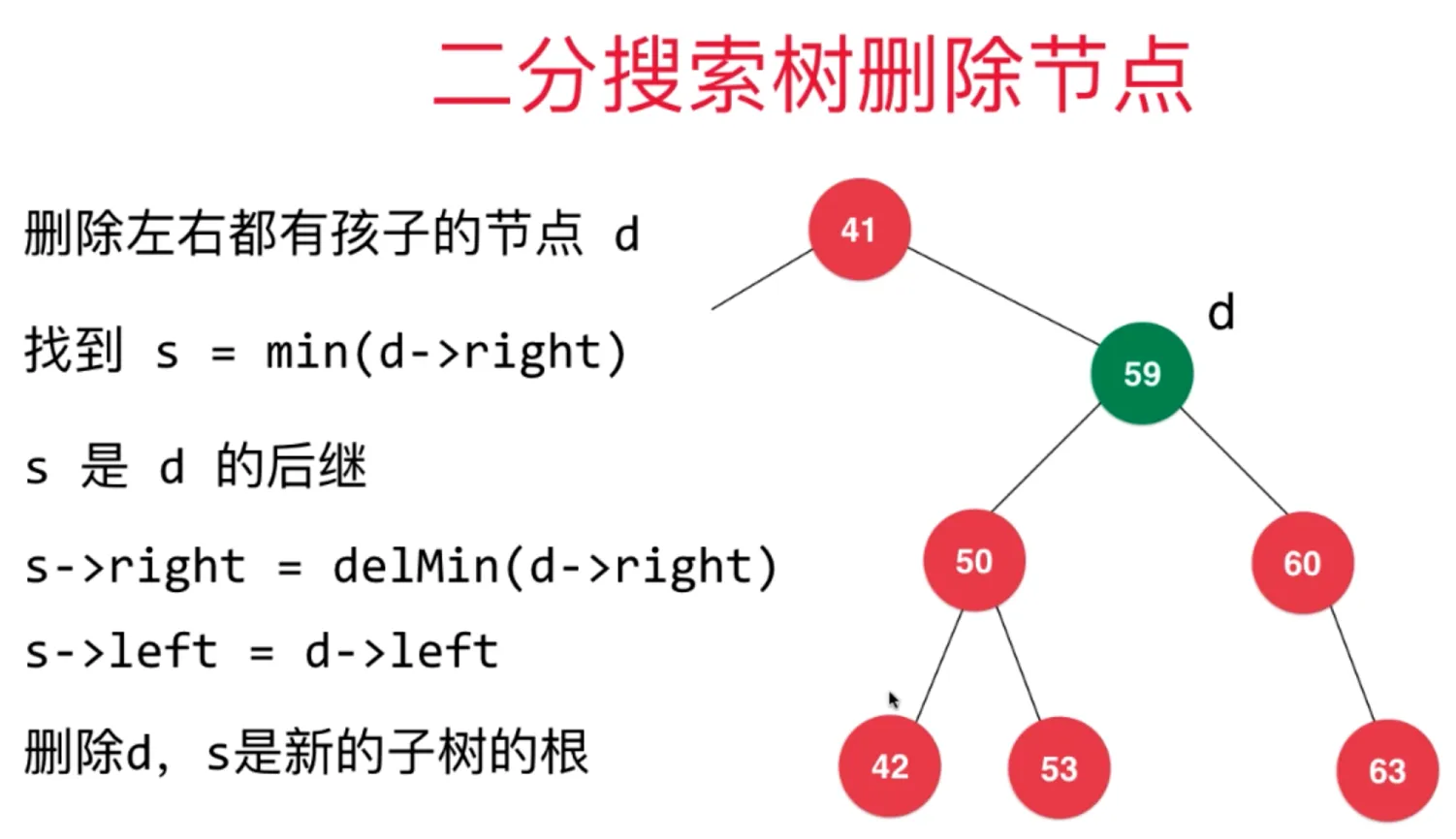
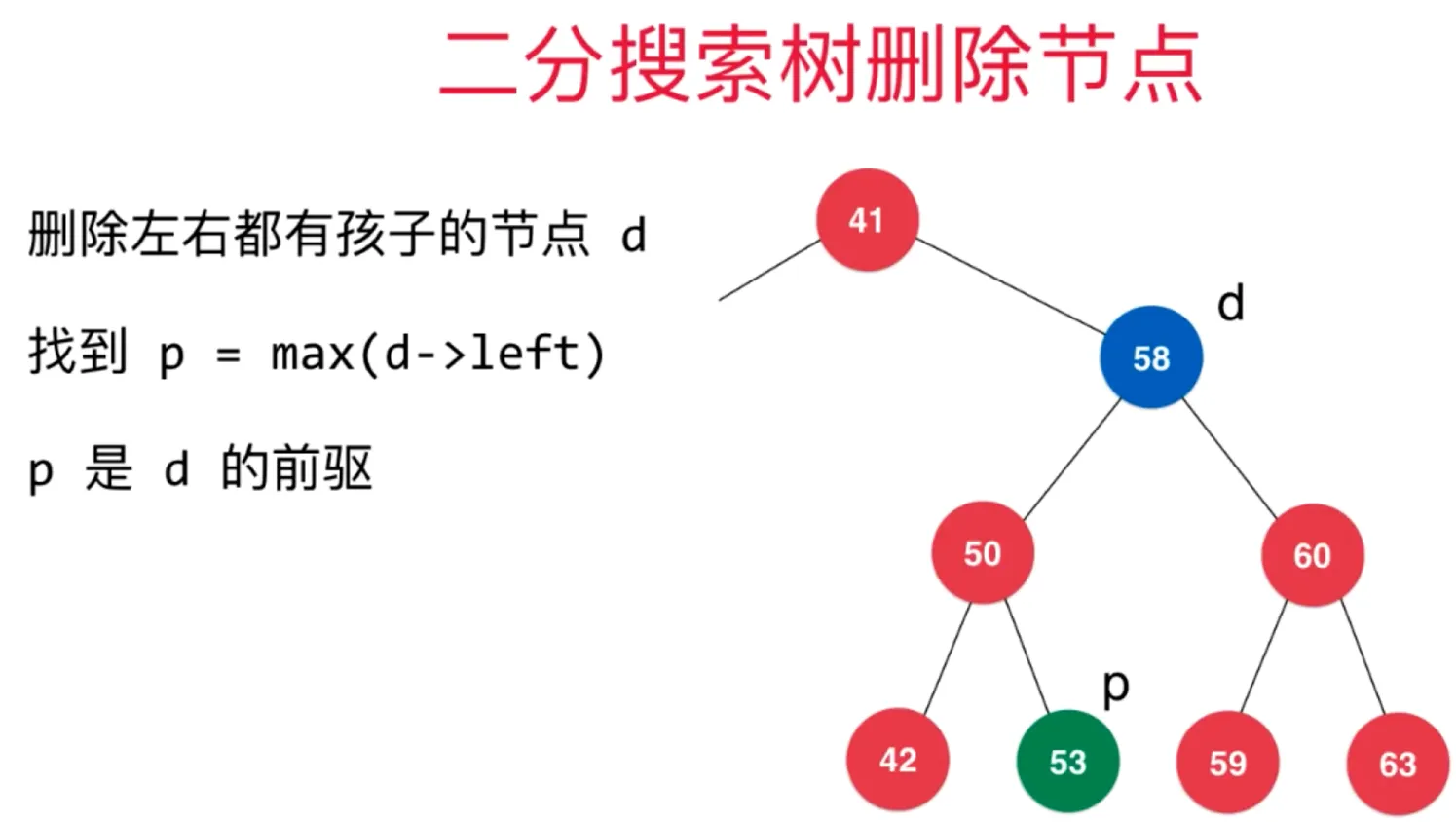
当然,这个节点 s 也可以是左子树中最大的节点 p,p = max(d->left)
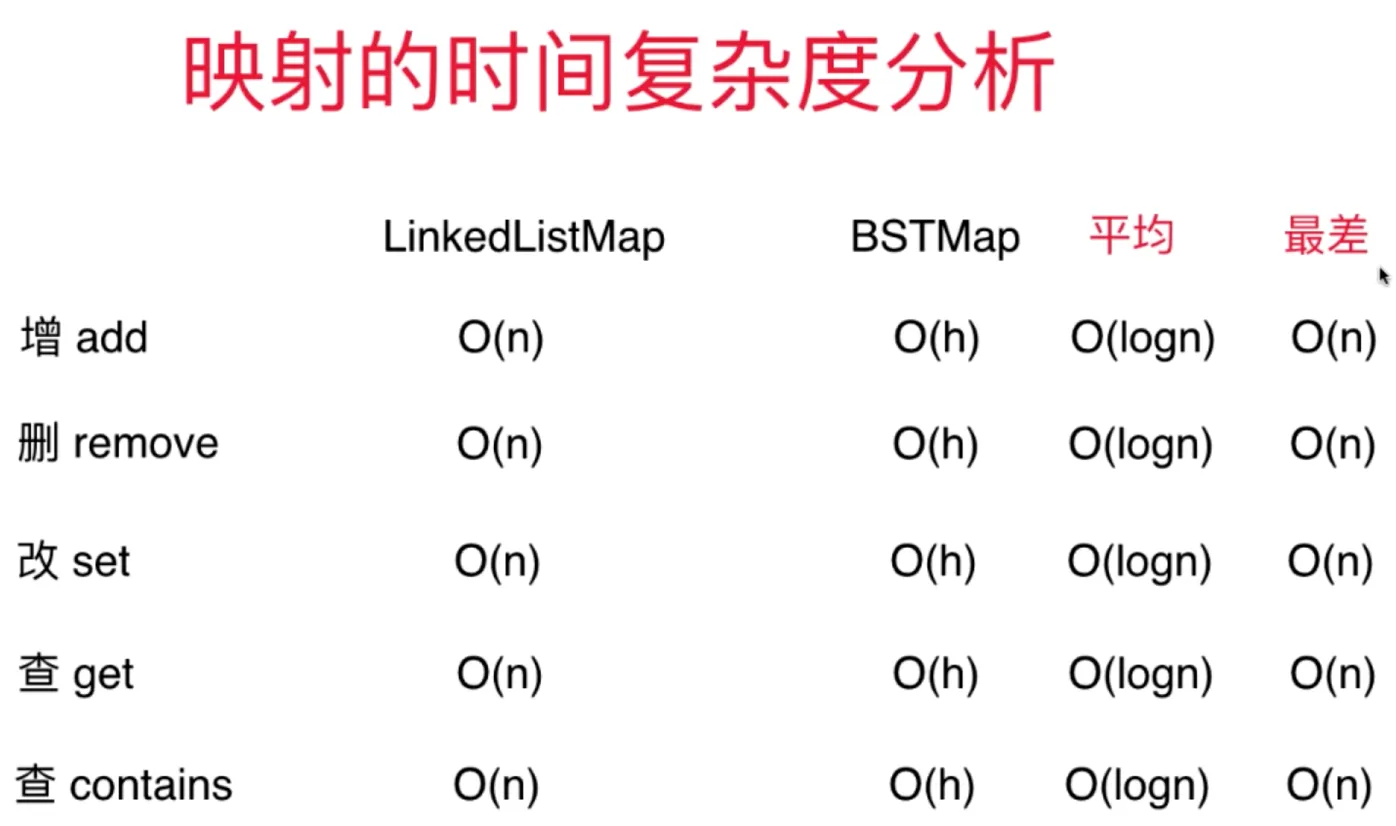
集合和映射 set and map

二分搜索树集合和链表集合的时间复杂度分析



优先队列
什么是优先队列? 普通队列:先进先出,后进后出 优先队列:出队顺序和入队顺序无关;和优先级有关
应用: 操作系统时间片调度 特点:队列中元素动态变化,动态优先级

堆
堆的性质
二叉堆是一棵完全二叉树(缺失的节点一定在右下侧)
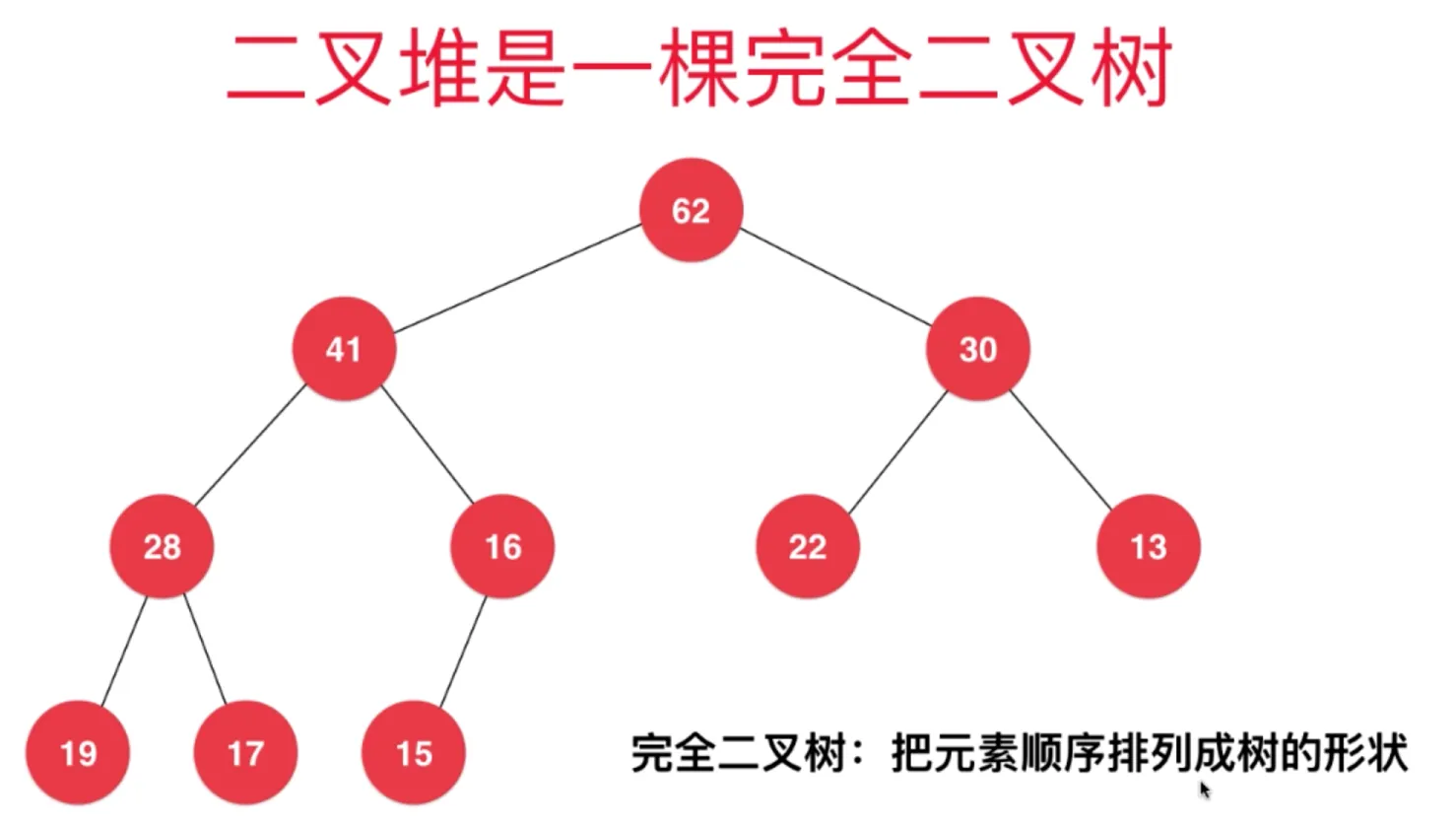
堆中的某个节点总是不大于其父节点的值(最大堆) (节点的值大于等于其子节点的值)
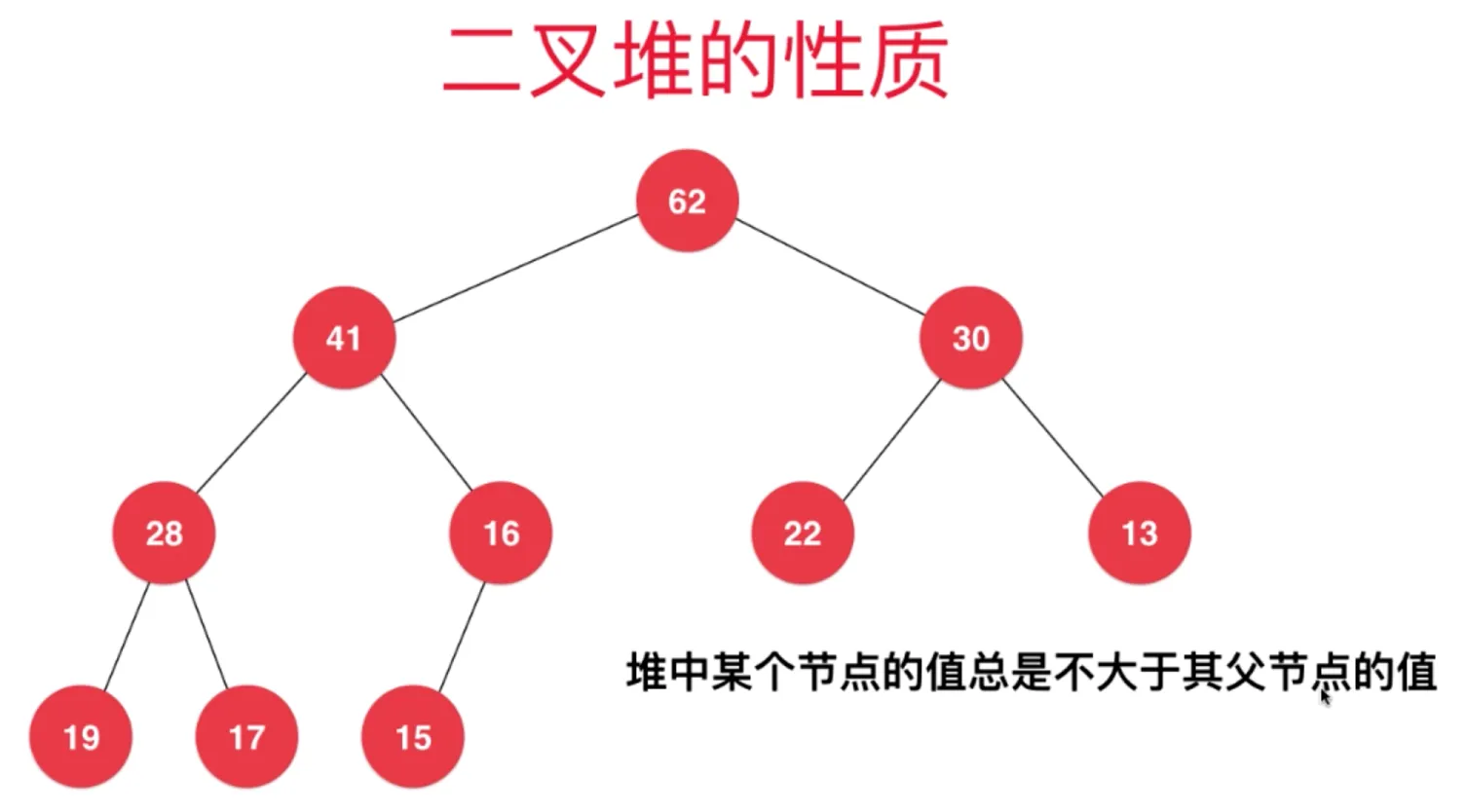
计算公式
用数组存储二叉堆
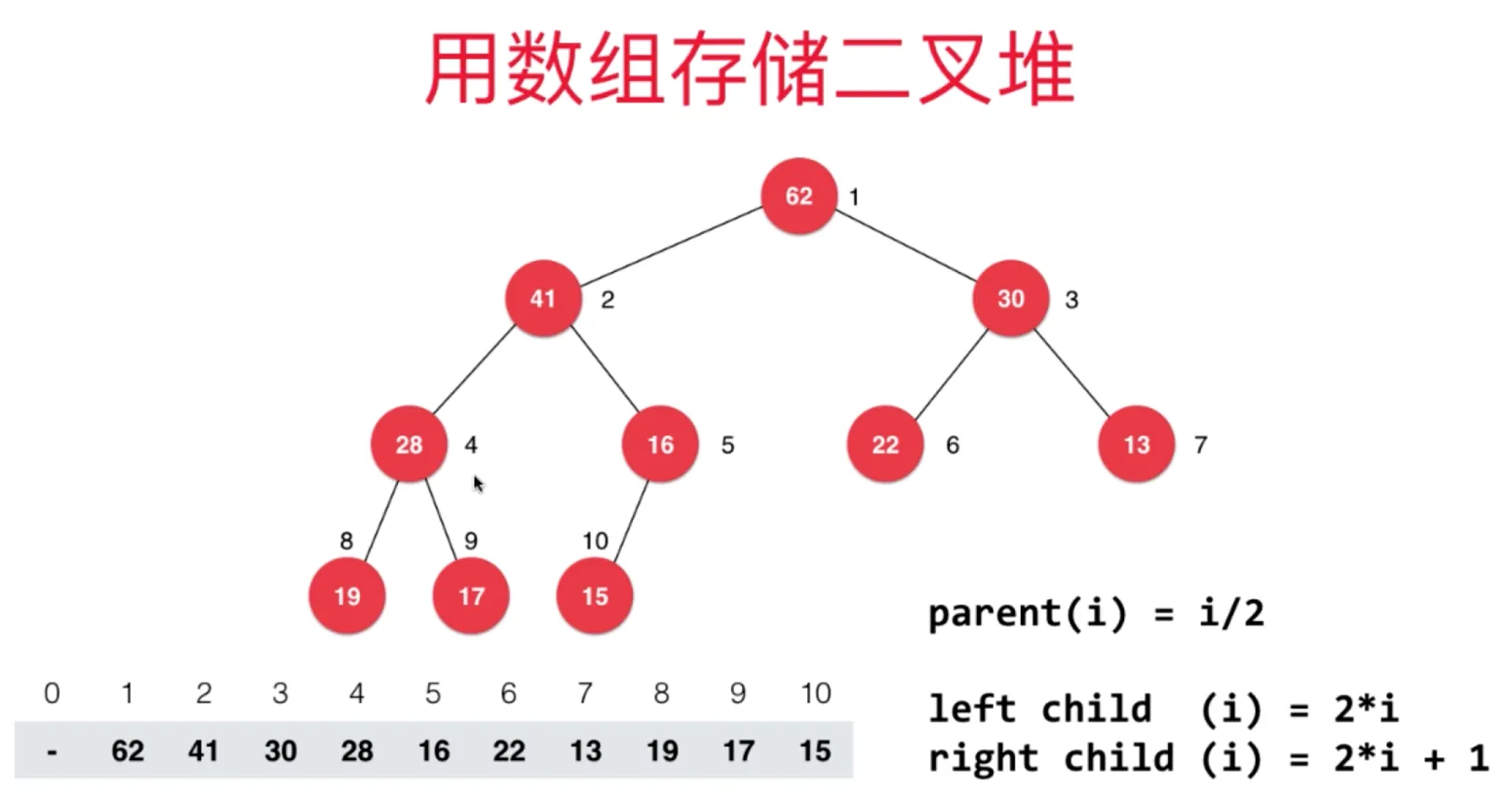 数组下标从0开始
数组下标从0开始
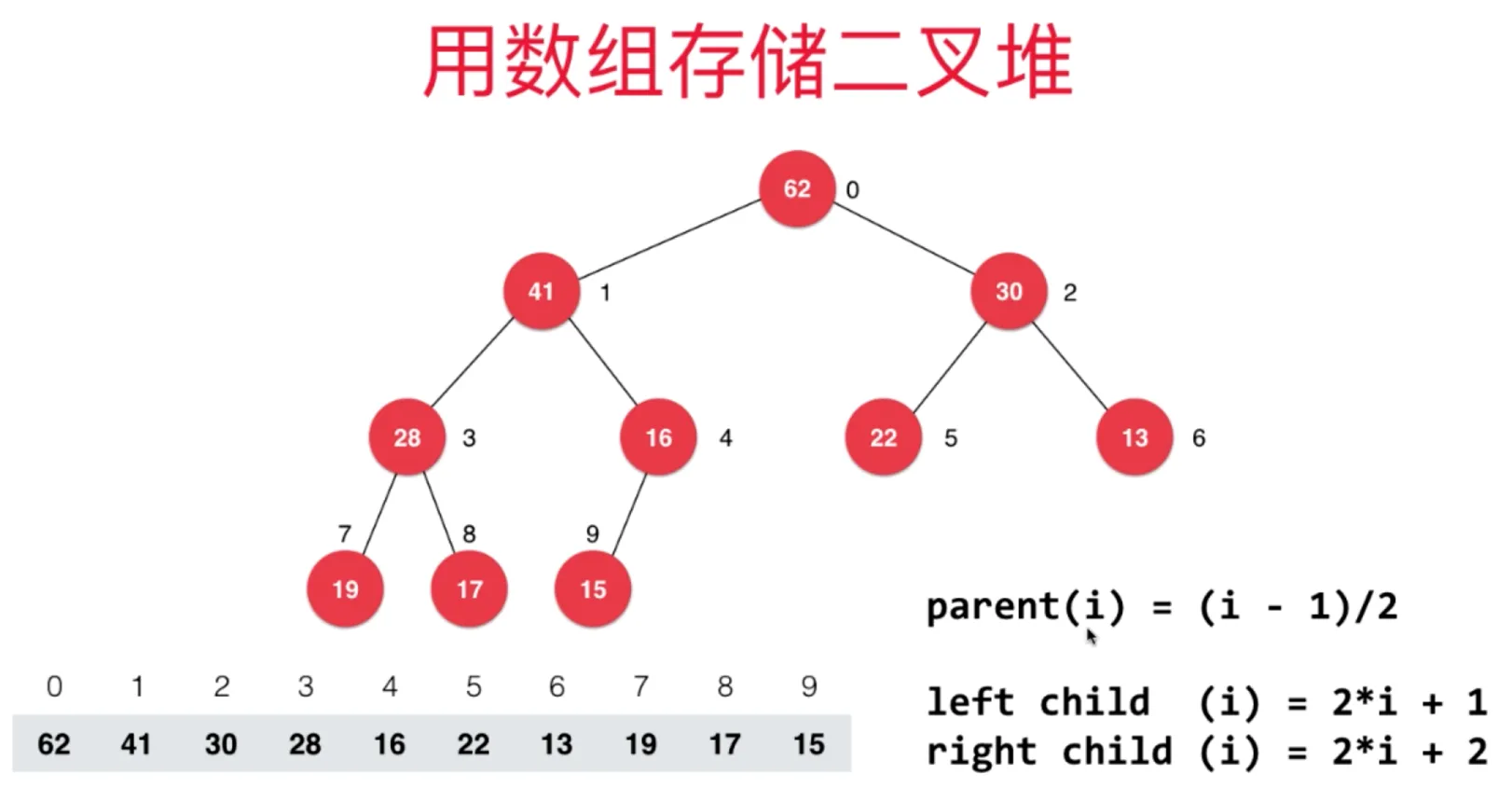
向堆中添加元素 sift up
- 向堆中添加元素,就是加入数组的末尾,
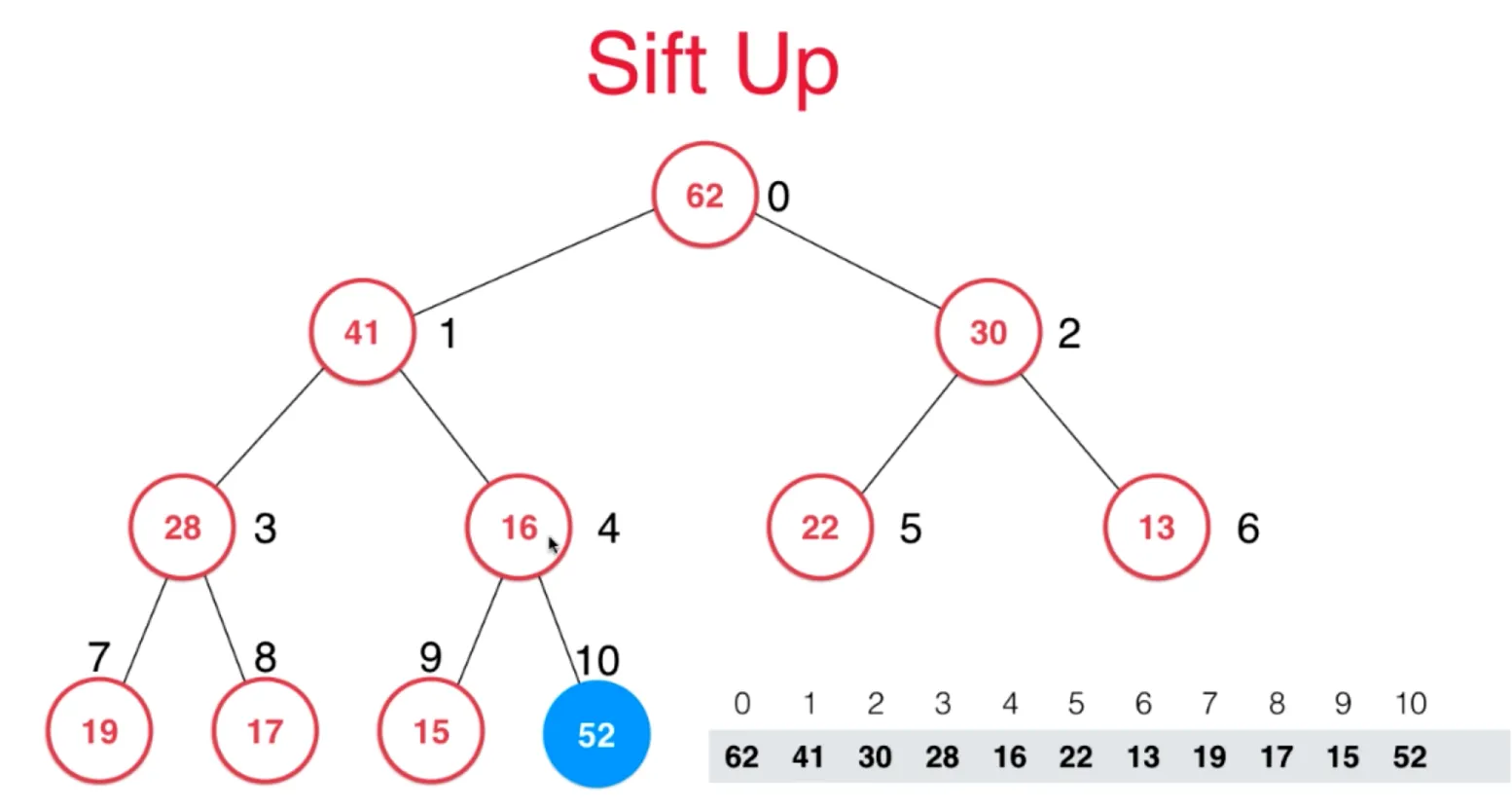
- 同时需要满足,父亲节点的值要大于它,如果不满足,交换它和父亲节点的位置
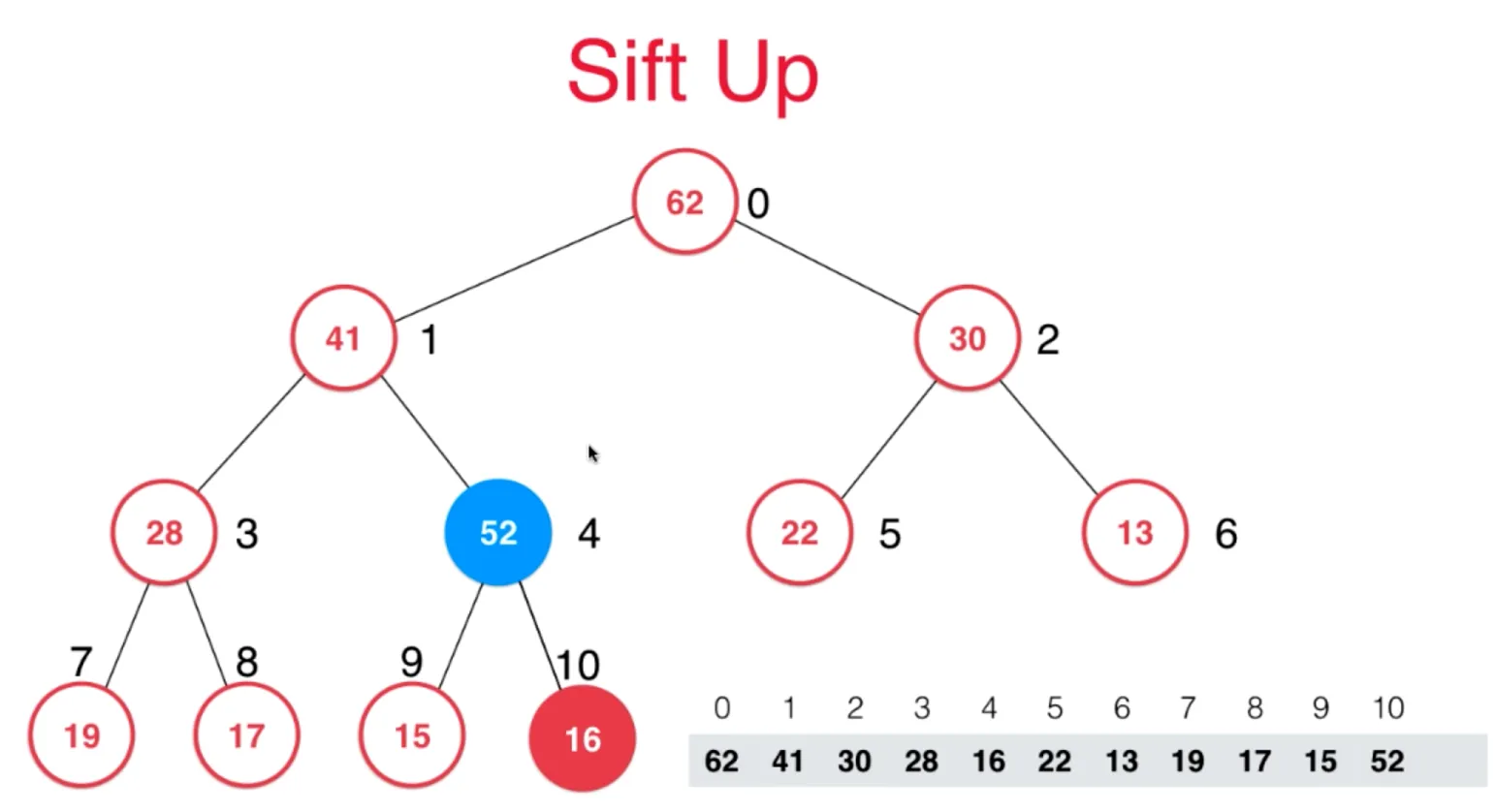 以此类推
以此类推
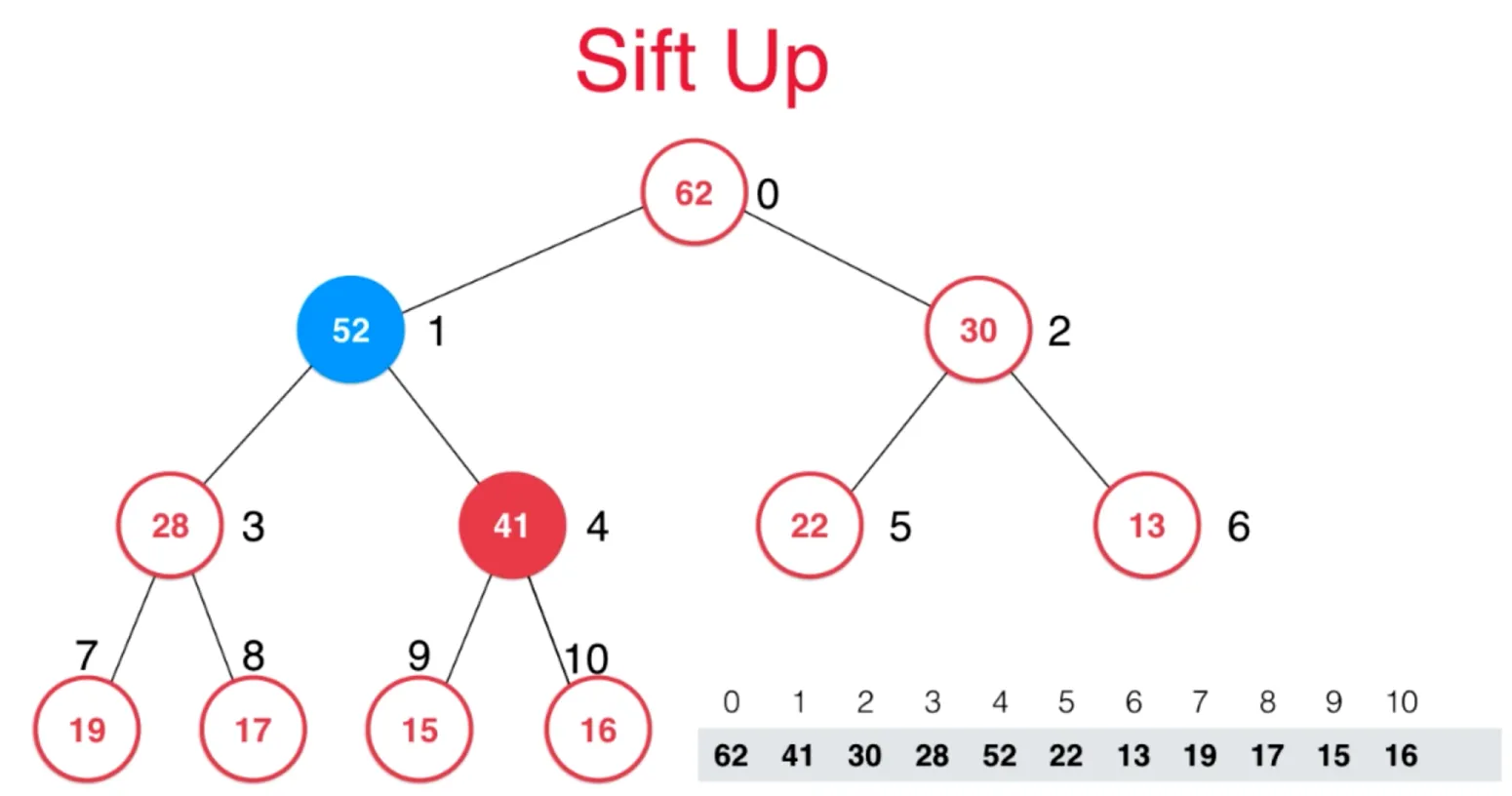
从堆中取出元素
只取出最大的元素(堆顶)
- 把堆中最后的元素放到堆顶(数组末尾放到开头),并删除末尾的元素,当前满足了完全二叉树的性质
- 当前这个元素不满足大于其它节点的性质,需要将其下沉,把它和他的左右子节点做比较,把左右节点中最大的元素和它做交换(当然也需要满足比它大)
堆的复杂度分析
插入取出都是 O(log(n))
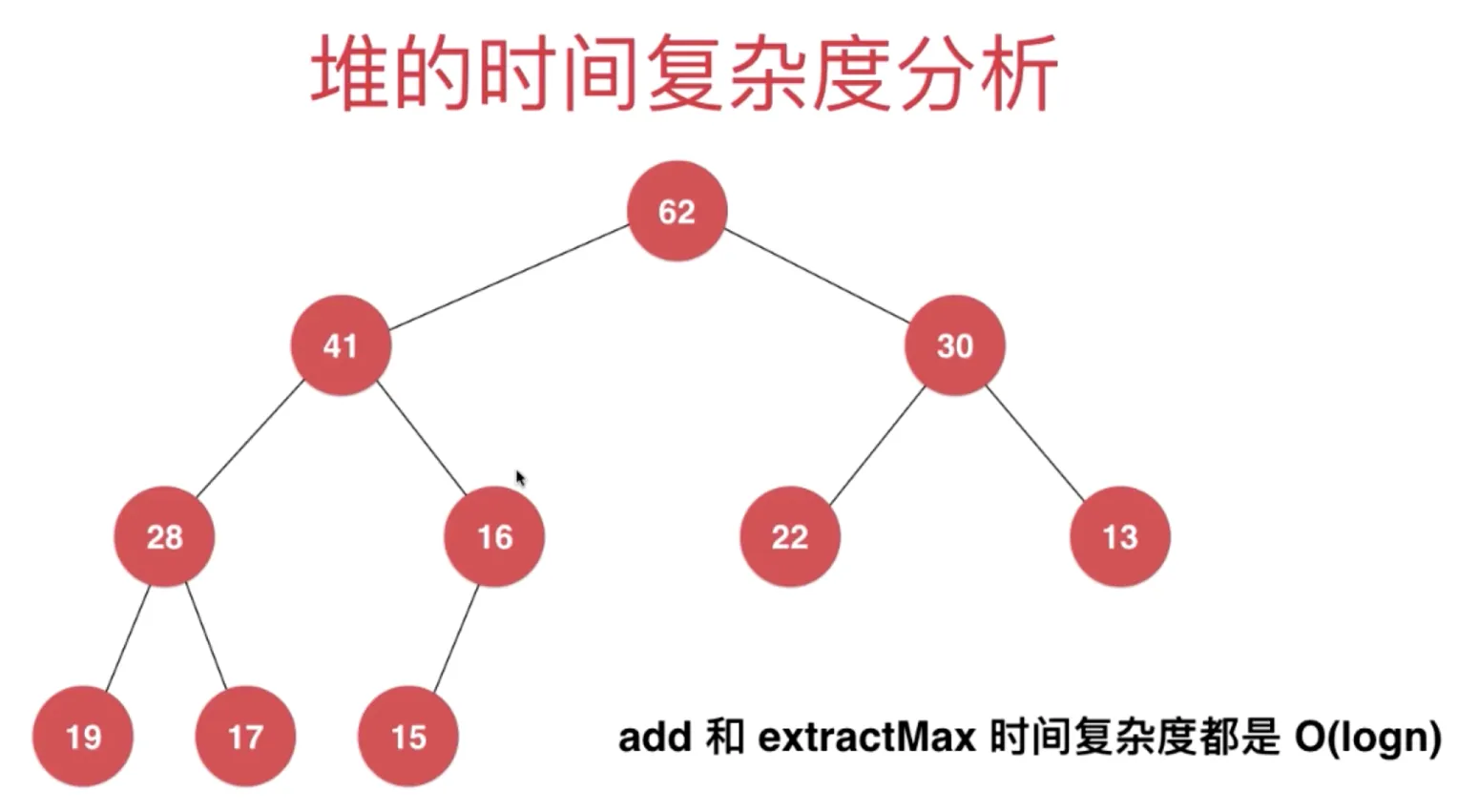
取出最大元素后,放入一个新的元素(replace)
实现: 可以直接将队中最大的元素替换后 sift down
将任意数组整理成堆的形状(heapify)
从最后一个非叶子节点开始(图中的22)向前 sift down
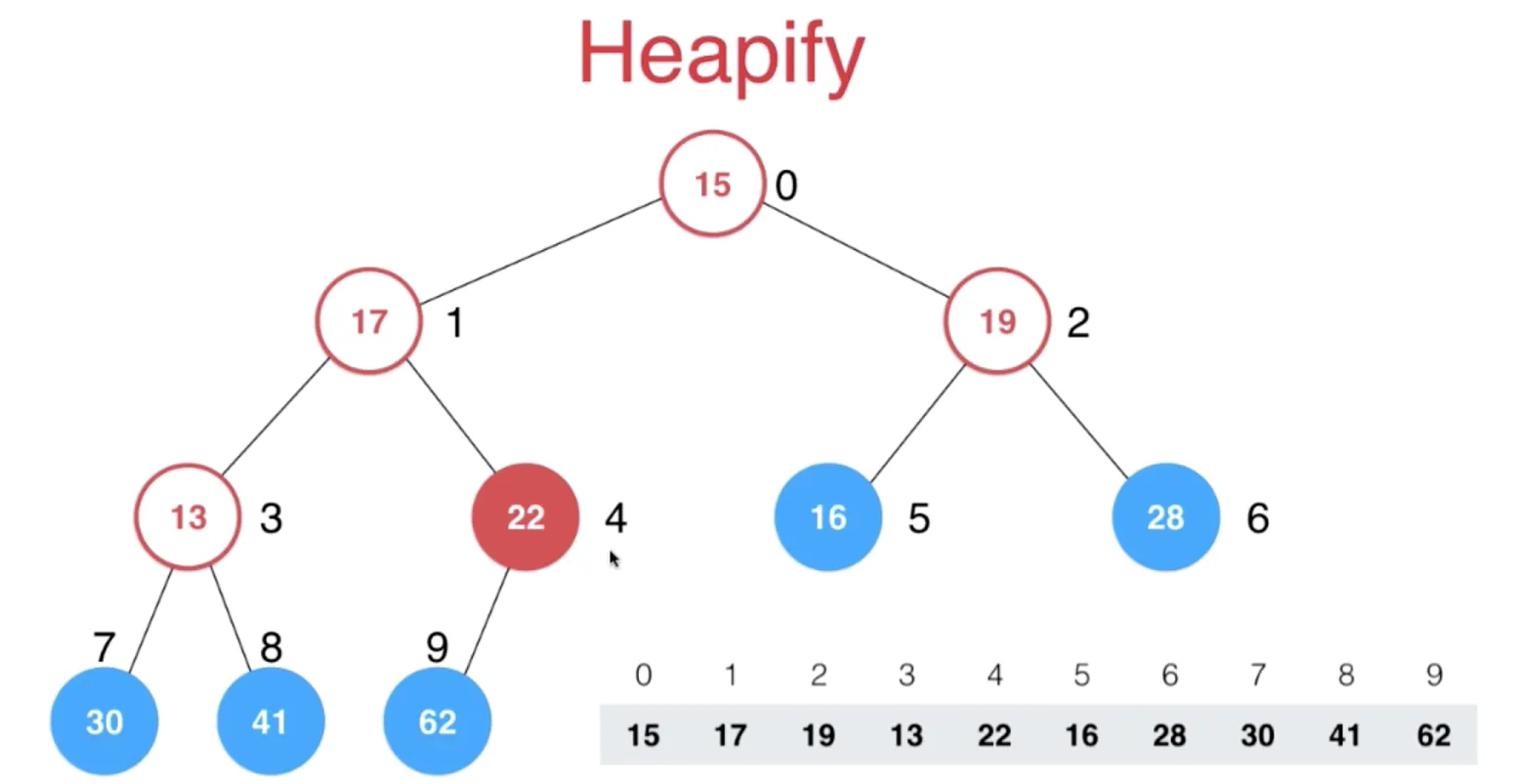
这个节点的计算方式是,最后一个节点(数组末尾 index=size-1)的父级节点((index-1)/2)

堆原地排序
- 堆中最大的元素在数组首位,将其和数组末尾元素交换位置
此时,数组的前半部分(最后一个元素之前)不满足最大堆性质

- 把现在开头元素 sift down, 这样前半部分又是最大堆

- 持续这个过程
由于没有开辟新空间,此时空间复杂度 O(1)
优先队列解决 topK 问题
在 N 个元素中选出最大的 K 个元素 在 N 个元素中选出最小的 K 个元素
select K 问题 — 找出第K大的元素(快速排序中处理过)


使用快排思想和使用优先队列思想解决 topK、selectK 问题比较:
快排:时间 O(n) 空间O(1)
优先队列:时间 O(nlogk) 空间O(k)
优先队列的优势:不需要一次性知道所有数据(数据流、极大规模数据)

冒泡排序法
比较相邻的两个元素(j, j+1)如果j大于j+1则交换两者位置,一直比较到末尾
算法复杂度 O(n^2)
public static <E extends Comparable<E>> void sort(E[] data) {
for (int i = 0; i + 1 < data.length; i++) {
for (int j = 0; j < data.length - i - 1; j++) {
if (data[j].compareTo(data[j + 1]) > 0) {
swap(data, j, j + 1);
}
}
}
}优化一,如果已经是有序的了,就不需要继续后面的冒泡了(全程没有交换位置)
public static <E extends Comparable<E>> void sort2(E[] data) {
for (int i = 0; i + 1 < data.length; i++) {
boolean isSwapped = false;
for (int j = 0; j < data.length - i - 1; j++) {
if (data[j].compareTo(data[j + 1]) > 0) {
swap(data, j, j + 1);
isSwapped = true;
}
}
if (!isSwapped) {
break;
}
}
}优化二,冒泡后,如果后面几个元素没有交换位置,说明它已经是有序的了,记录最后交换的索引,下轮冒泡跳过这些有序的值
public static <E extends Comparable<E>> void sort3(E[] data) {
for (int i = 0; i + 1 < data.length; ) {
int lastSwappedIndex = 0;
for (int j = 0; j < data.length - i - 1; j++) {
if (data[j].compareTo(data[j + 1]) > 0) {
swap(data, j, j + 1);
lastSwappedIndex = j + 1;
}
}
// if (lastSwappedIndex == 0) {
// // 没有发生过交换,数组有序
// break;
// }
i = data.length - lastSwappedIndex;
}
}希尔排序法
插入排序:从索引 1 开始,和它前面的元素比较,如果大于就不动,如果小于则交换位置 越有序的元素交换次数越少,完全有序的比较一遍就可以了,复杂度 O(n)
基本思想:让数据越来越有序
冒泡排序法,相邻两个元素如果是逆序对就交换位置
希尔排序法:不能只处理相邻的逆序对
图中两个颜色一样的分为一组 每组索引相差4,分别对每组进行插入排序(如果左大于右就交换位置)

一轮希尔排序后

把整个数组按距离为 2 进行分组

排序后

按间隔为 1 进行分组,就是数组本身,进行插入排序

public static <E extends Comparable<E>> void sort(E[] data) {
int h = data.length / 2;
while (h >= 1) {
for (int start = 0; start < h; start++) {
// 对 data[start, start+h, start+2h, start+3h, ...] 进行插入排序
for (int i = start + h; i < data.length; i += h) {
E t = data[i];
int j;
for (j = i; j - h >= 0 && t.compareTo(data[j - h]) < 0; j -= h) {
data[j] = data[j - h];
}
data[j] = t;
}
}
h = h / 2;
}
}希尔排序性能 分析


代码优化:不显式拆分子数组,每轮对前面间隔 h 元素做比较
public static <E extends Comparable<E>> void sort2(E[] data) {
int h = data.length / 2;
while (h >= 1) {
// 对 data[h, n) 进行插入排序
for (int i = h; i < data.length; i += h) {
E t = data[i];
int j;
for (j = i; j - h >= 0 && t.compareTo(data[j - h]) < 0; j -= h) {
data[j] = data[j - h];
}
data[j] = t;
}
h = h / 2;
}
}步长序列
 超参数
超参数
public static <E extends Comparable<E>> void sort3(E[] data) {
int h = 1;
while (h < data.length) {
h = h * 3 + 1;
// 1, 4, 13, 40
}
while (h >= 1) {
// 对 data[h, n) 进行插入排序
for (int i = h; i < data.length; i += h) {
E t = data[i];
int j;
for (j = i; j - h >= 0 && t.compareTo(data[j - h]) < 0; j -= h) {
data[j] = data[j - h];
}
data[j] = t;
}
h = h / 3;
}
}基于比较的排序算法总结


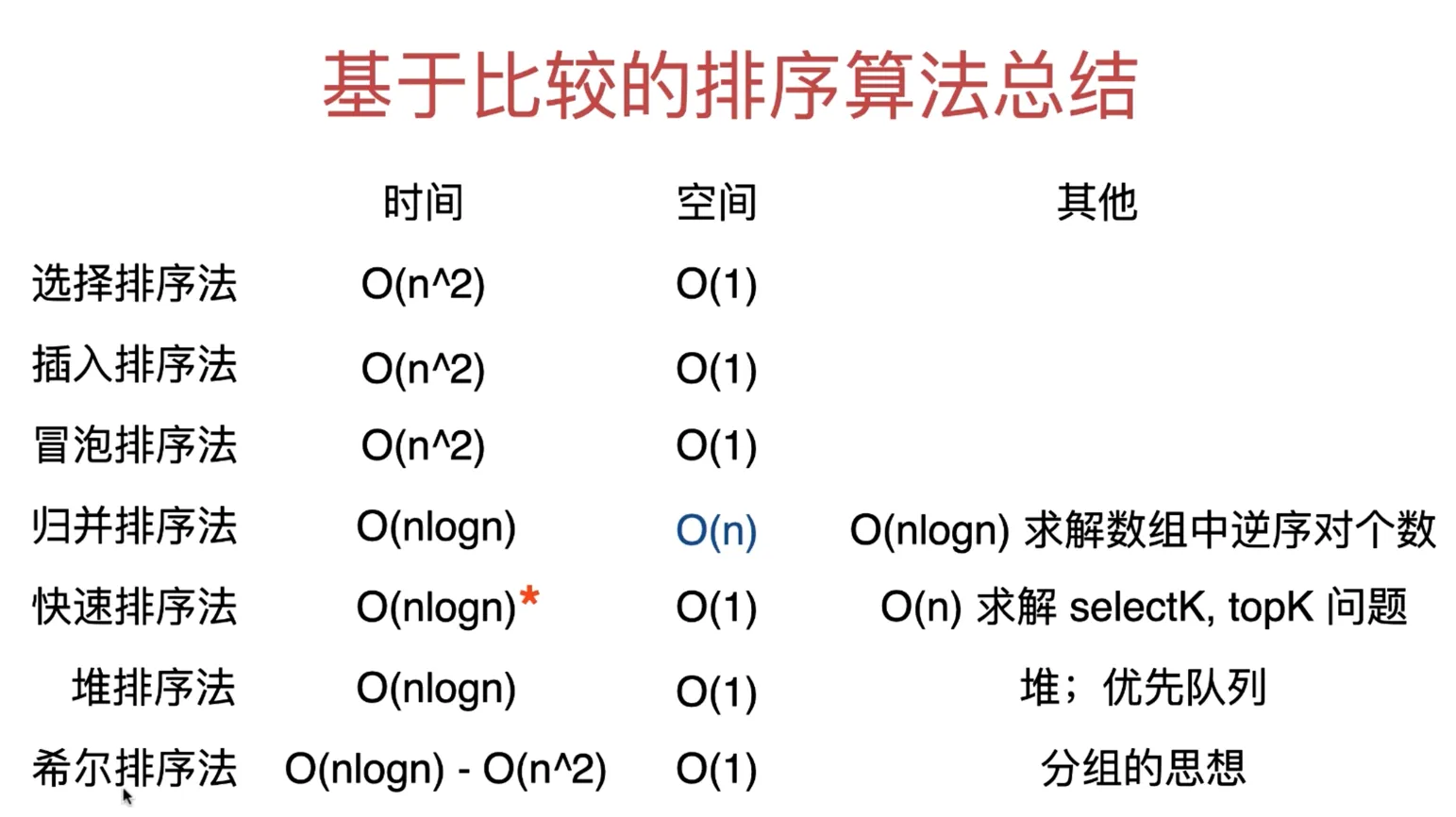
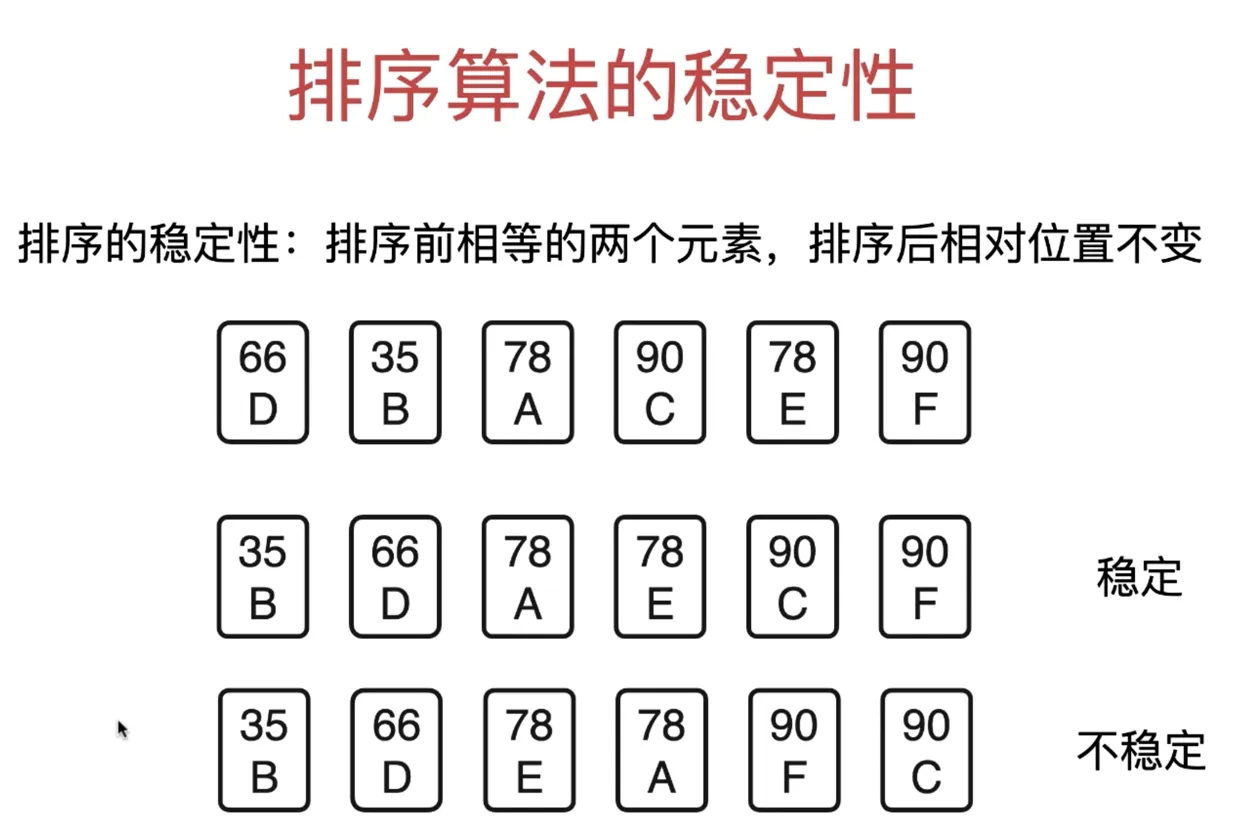
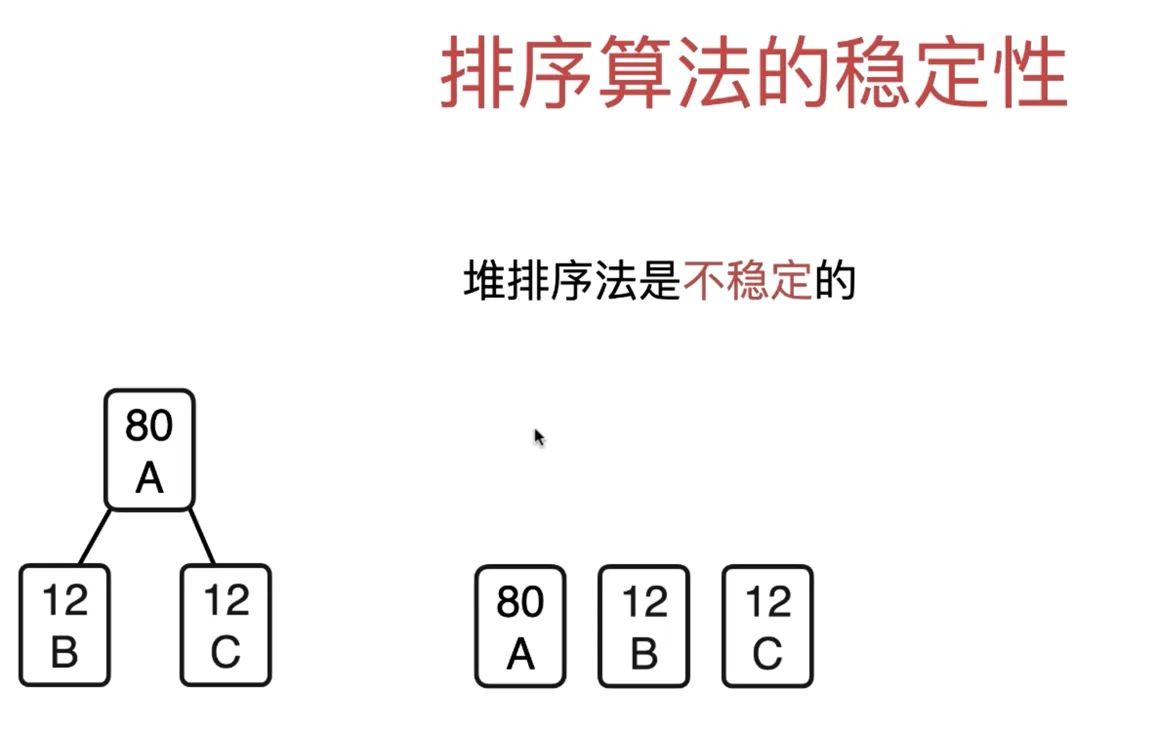
排序算法的稳定性
排序算法的稳定性:排序前相等的两个元素,排序后相对位置不变

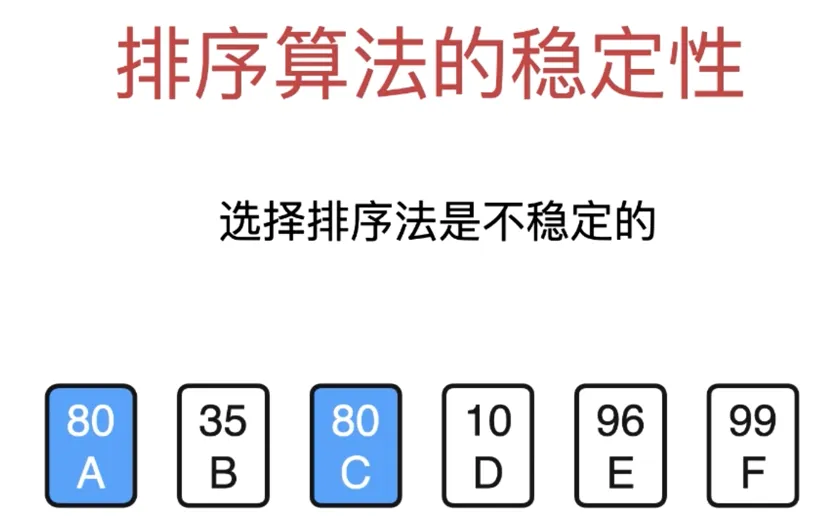
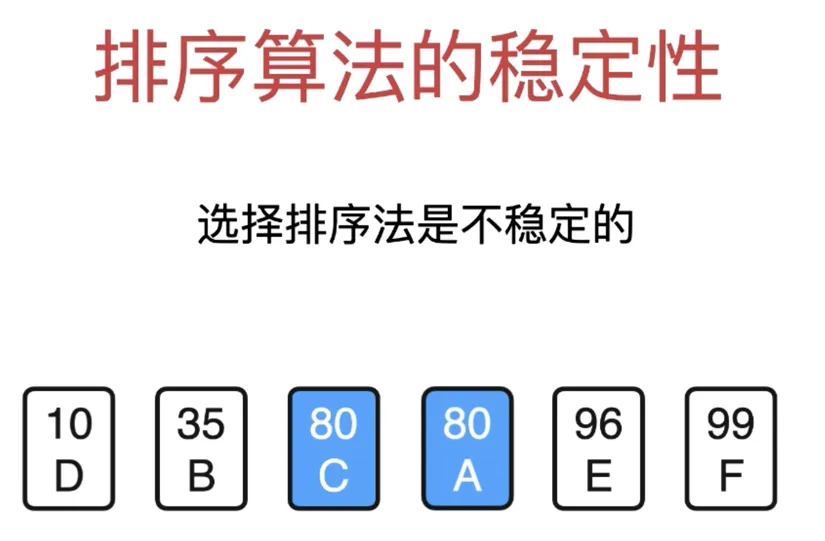
选择排序是不稳定的
插入排序法是稳定的(依赖具体实现)
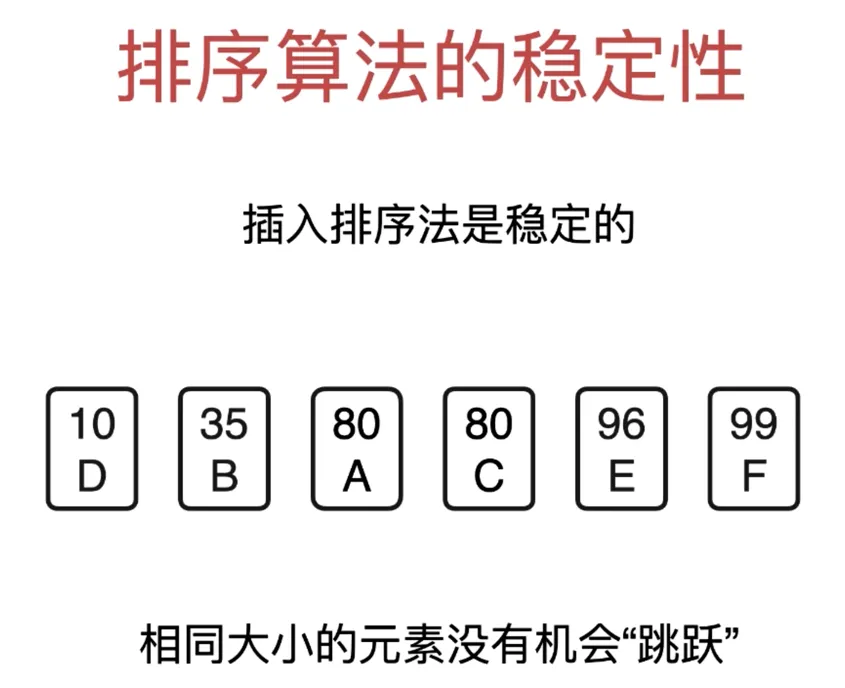

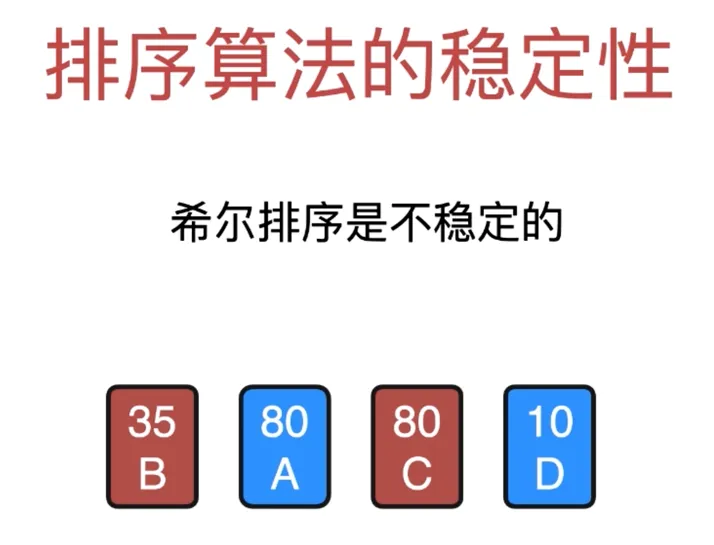
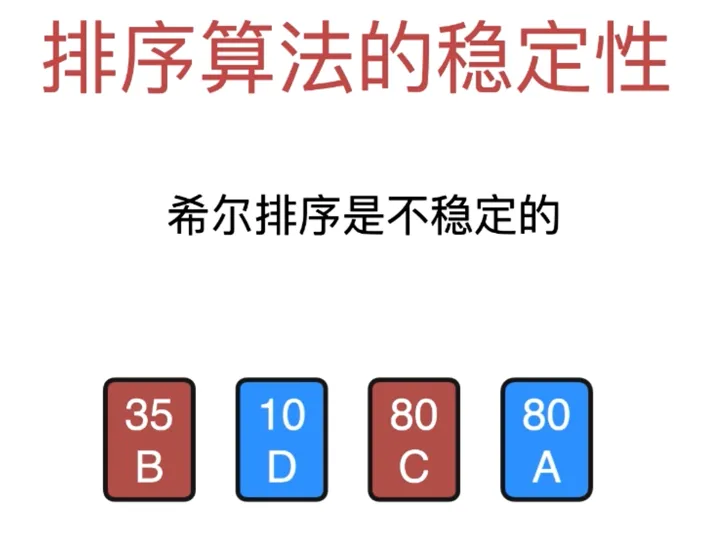
希尔排序是不稳定的
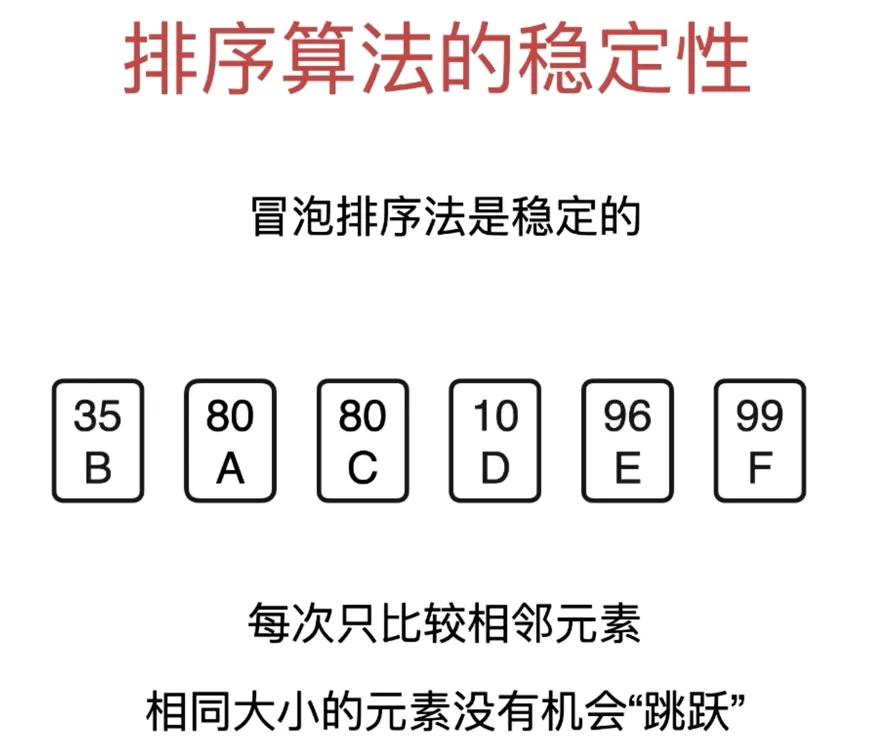
冒泡排序法是稳定的







线段树(区间树)
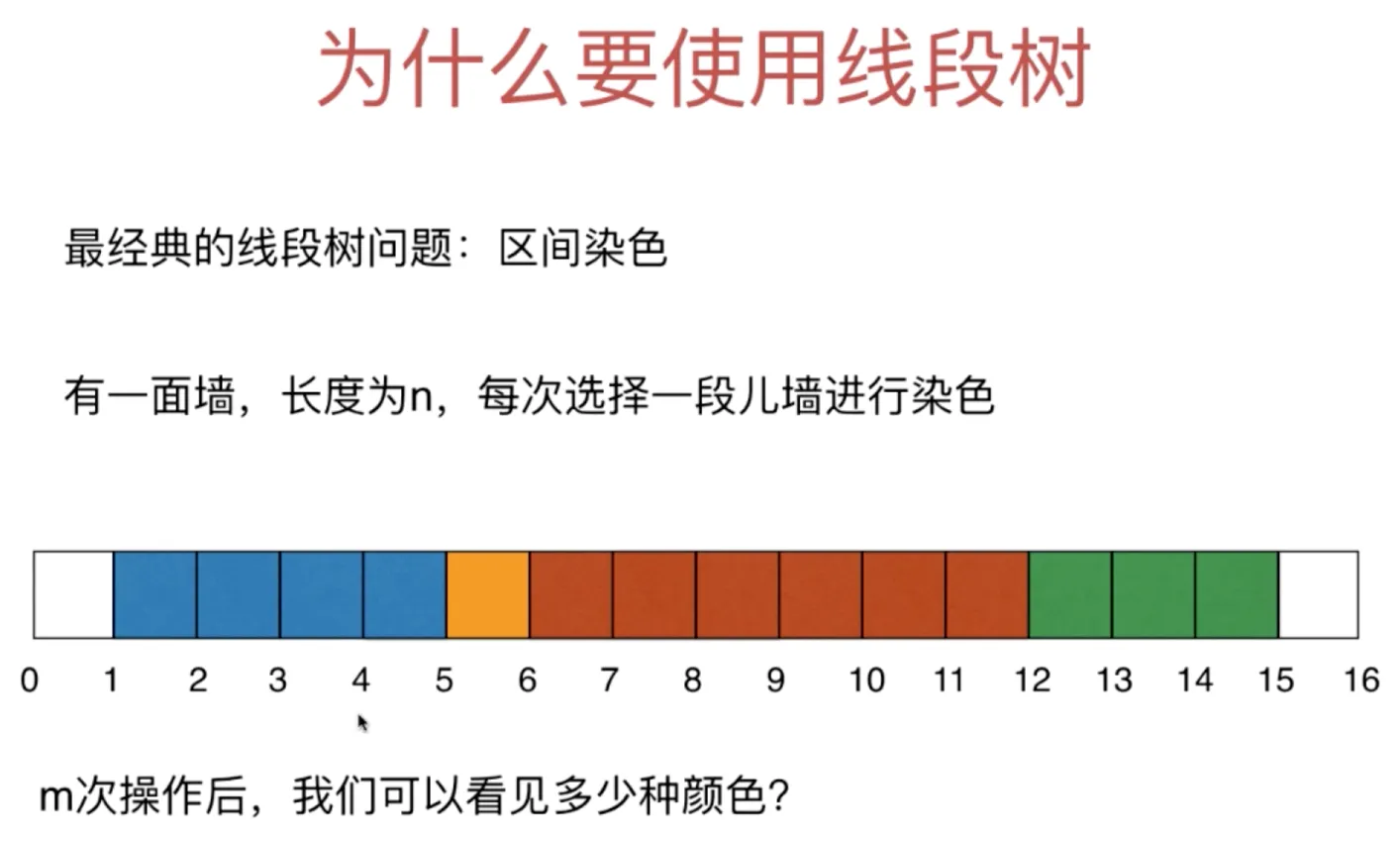

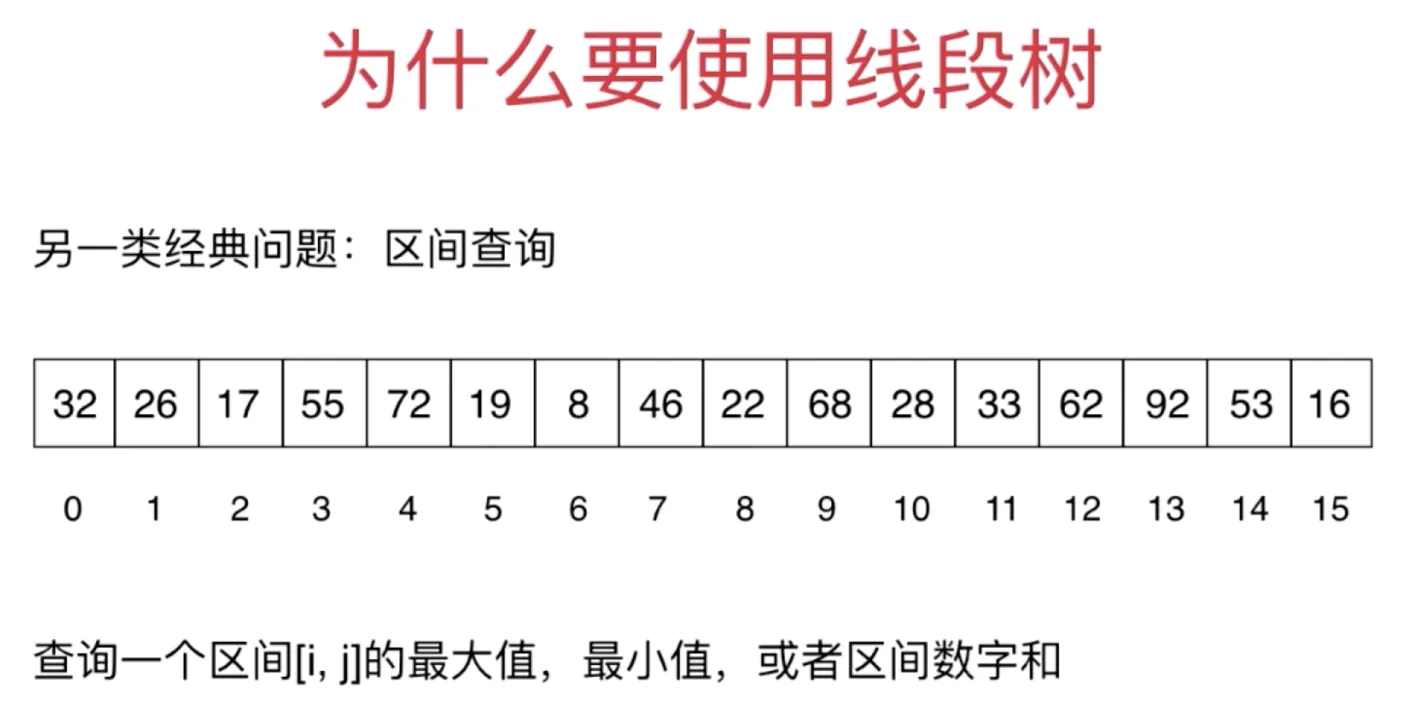 这类问题,数组复杂度 O(n) 线段树 O(log(n))
这类问题,数组复杂度 O(n) 线段树 O(log(n))
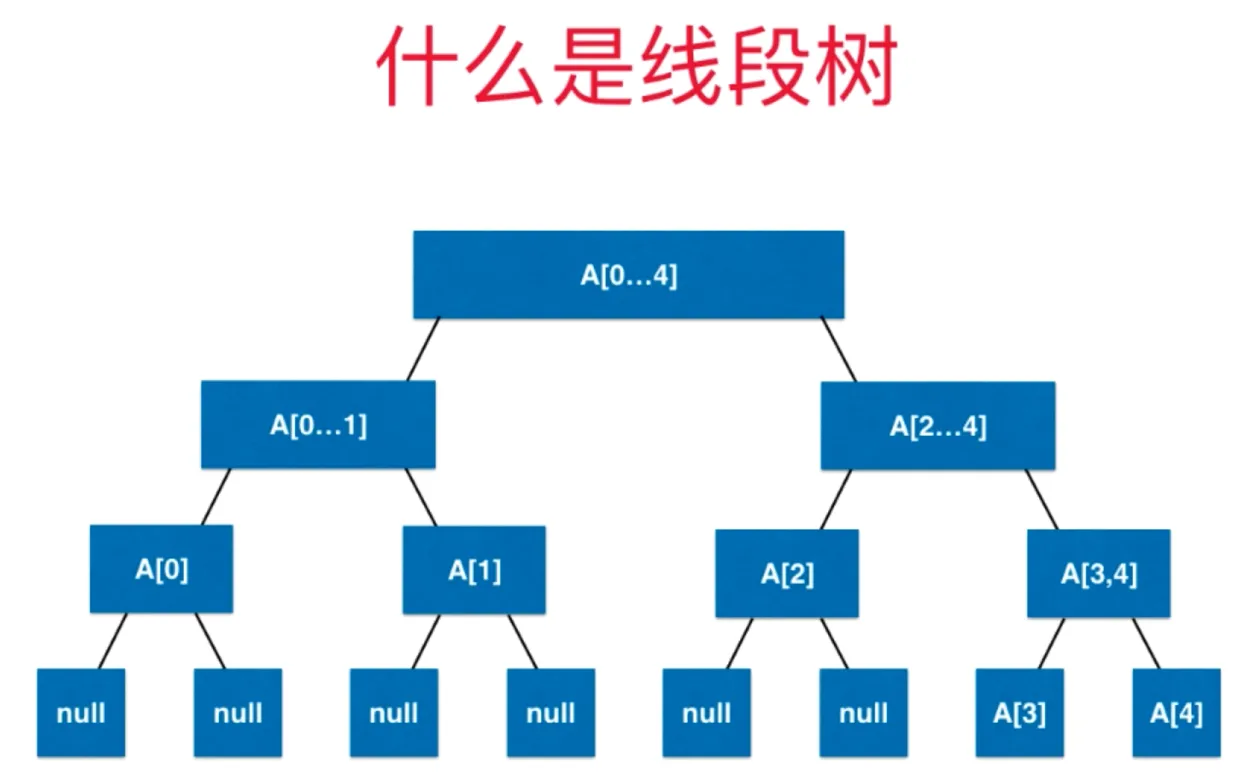
对于二叉树中的每一个节点,存储的是一个线段/区间的信息
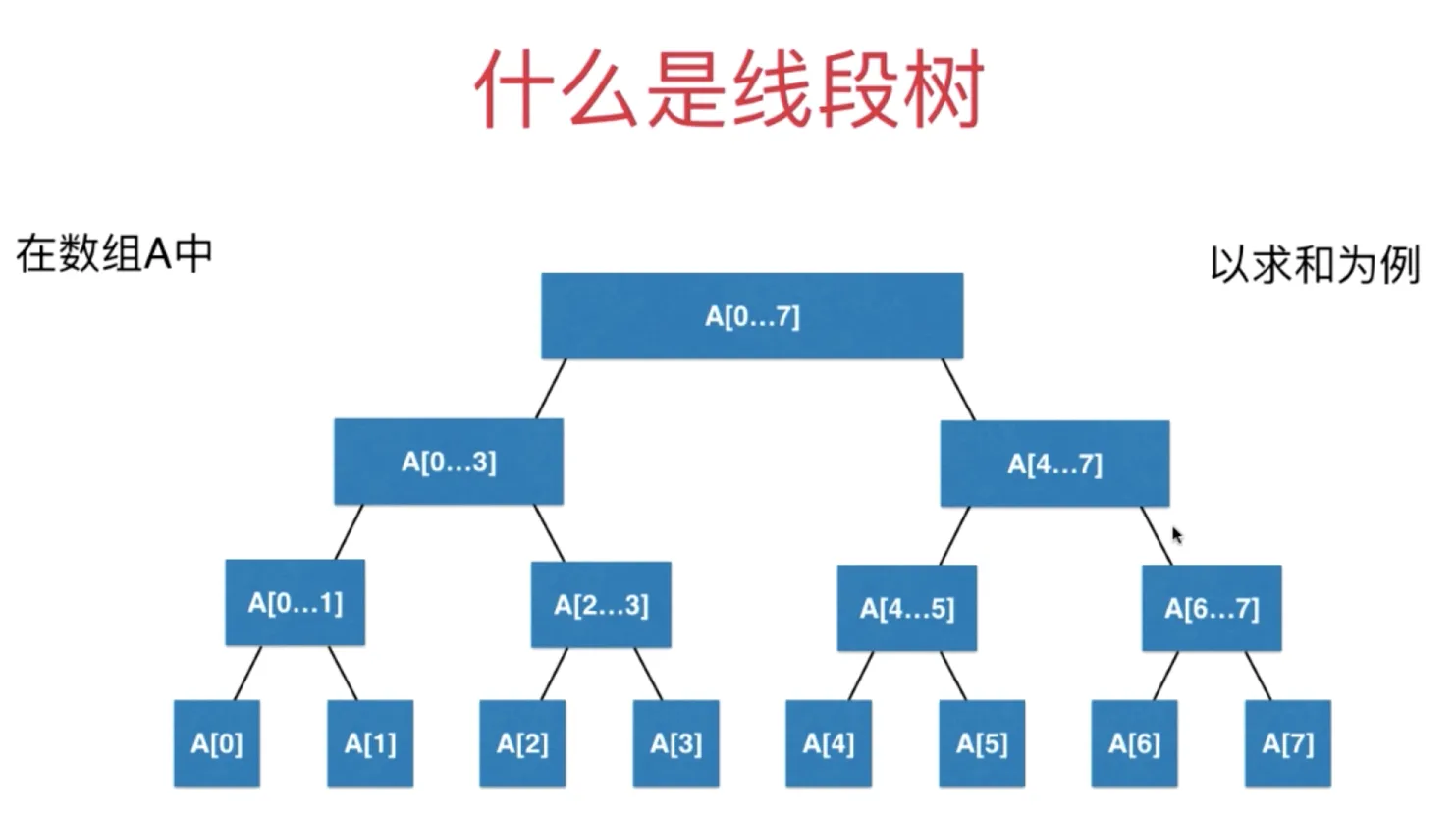
平衡二叉树,对于整棵树来说,最大深度和最小深度的差最多为 1
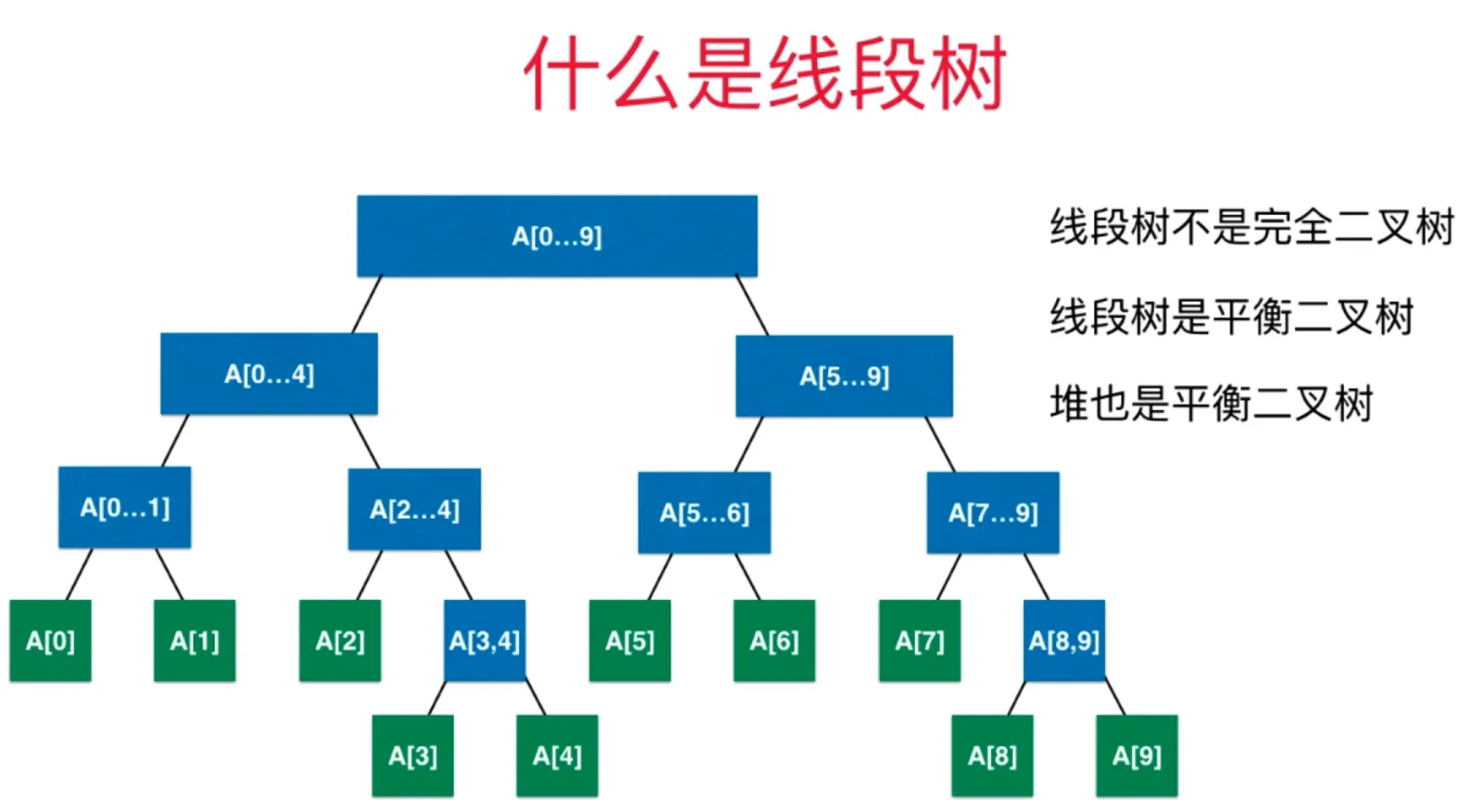
如果区间有 n 个元素,数组表示需要多少节点?

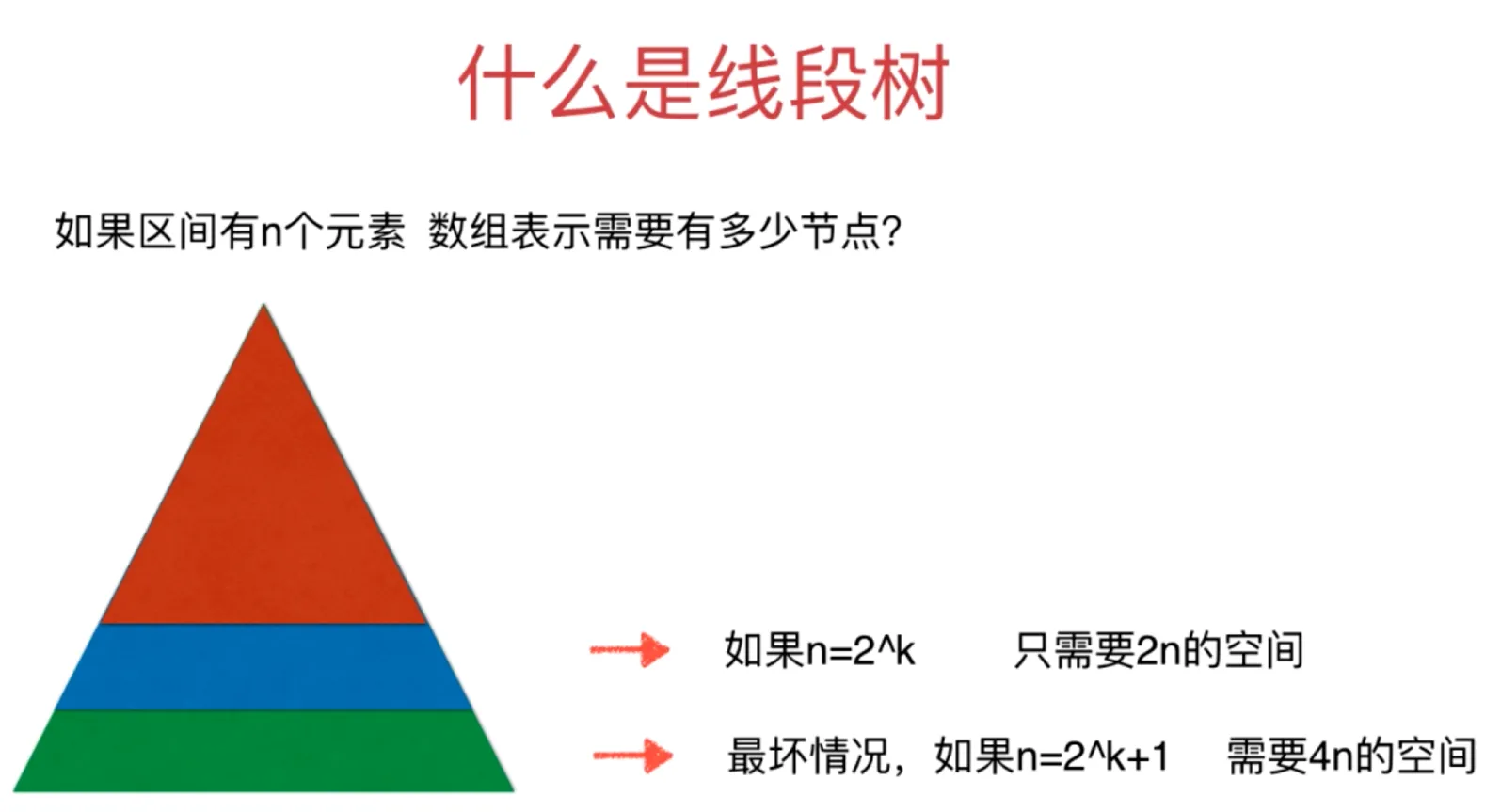
 最坏情况会有一半的空间是浪费的
最坏情况会有一半的空间是浪费的
查询 [2, 5]
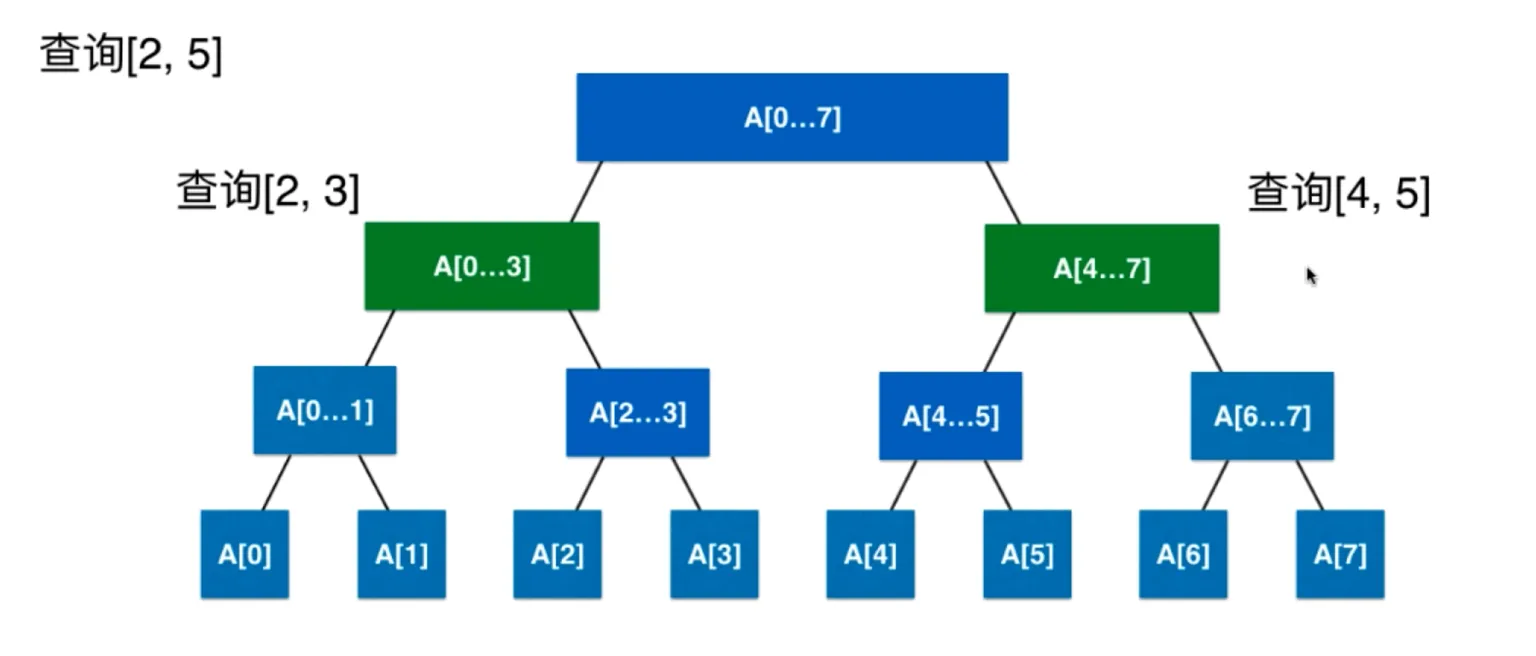
LeetCode 303 和 307 号问题
Trie 字典树 前缀树

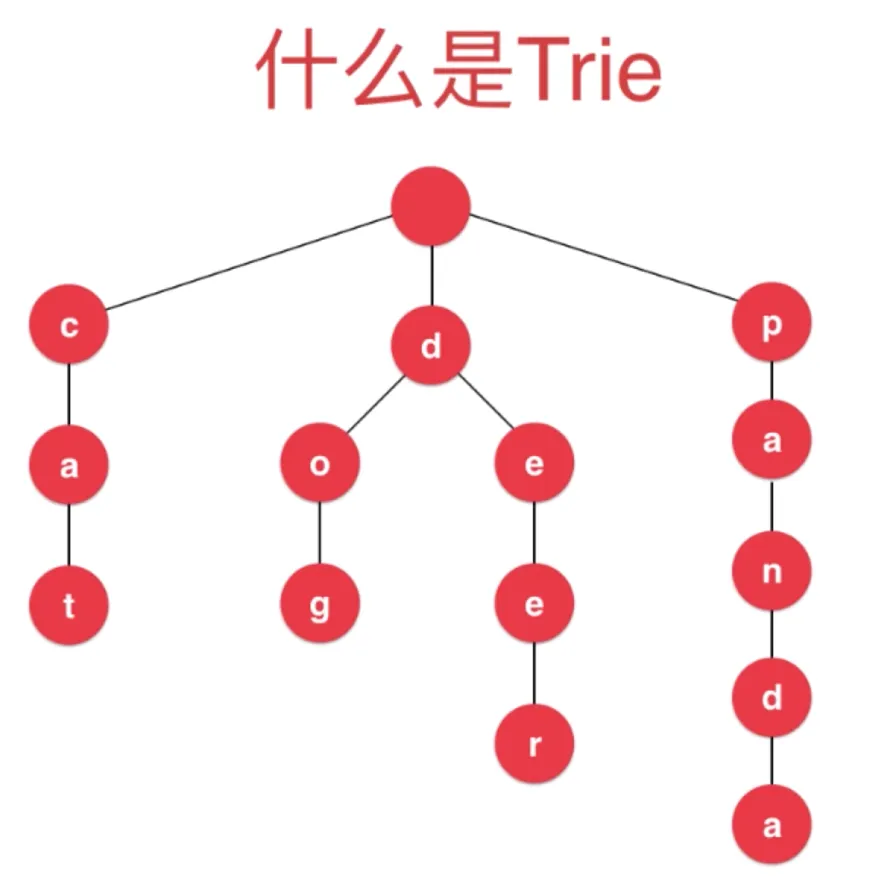
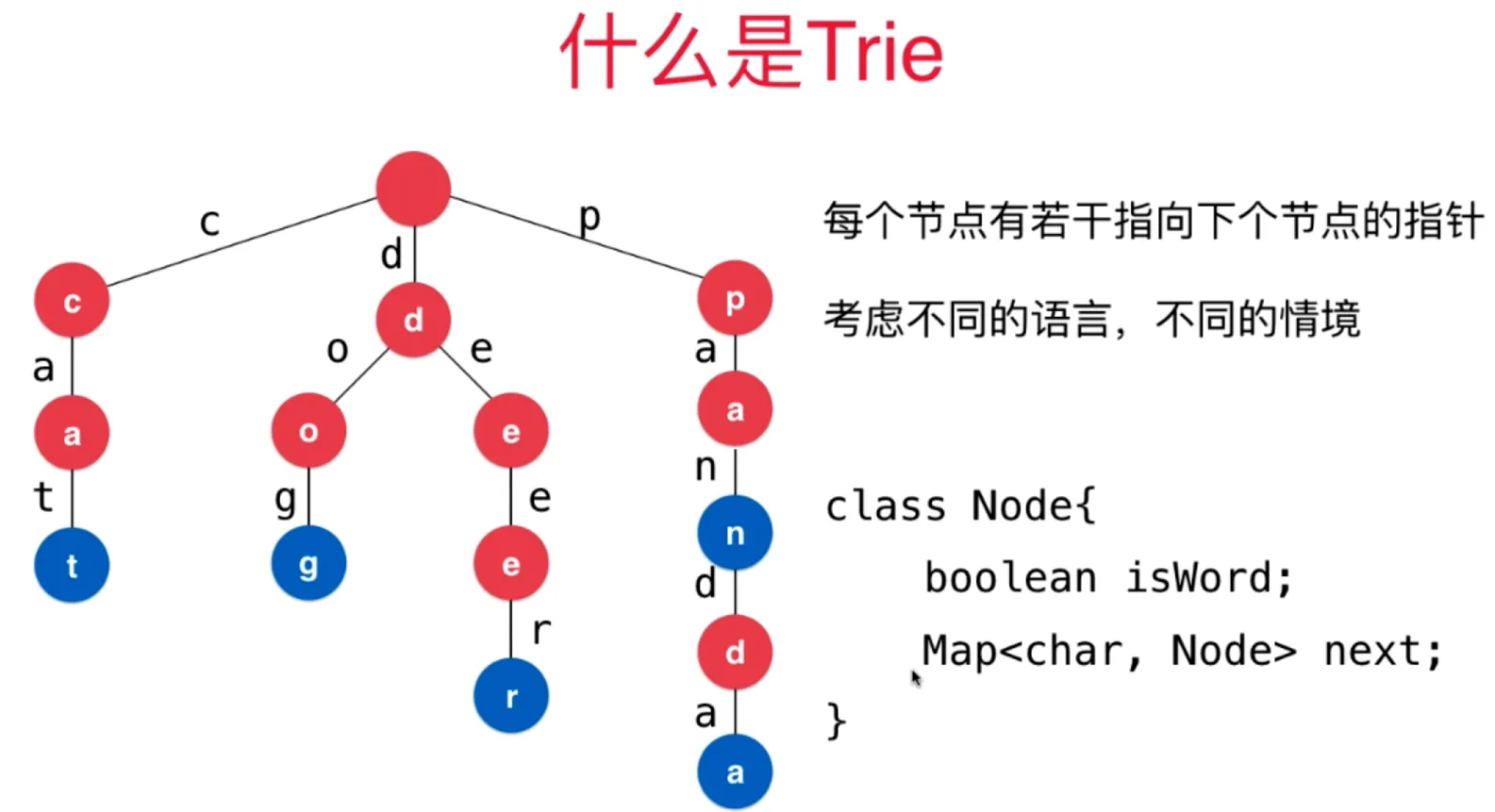
并查集 Union Find
连接问题 网络节点中的连接状态
- 网络是一个抽象的概念:用户之间形成的网络 数学中的集合类实现
 并查集内部为每个数据赋予一个编号(下图 0-9)
对于每一个元素,并查集存储了它所属集合的id(下图下半部分)
并查集内部为每个数据赋予一个编号(下图 0-9)
对于每一个元素,并查集存储了它所属集合的id(下图下半部分)
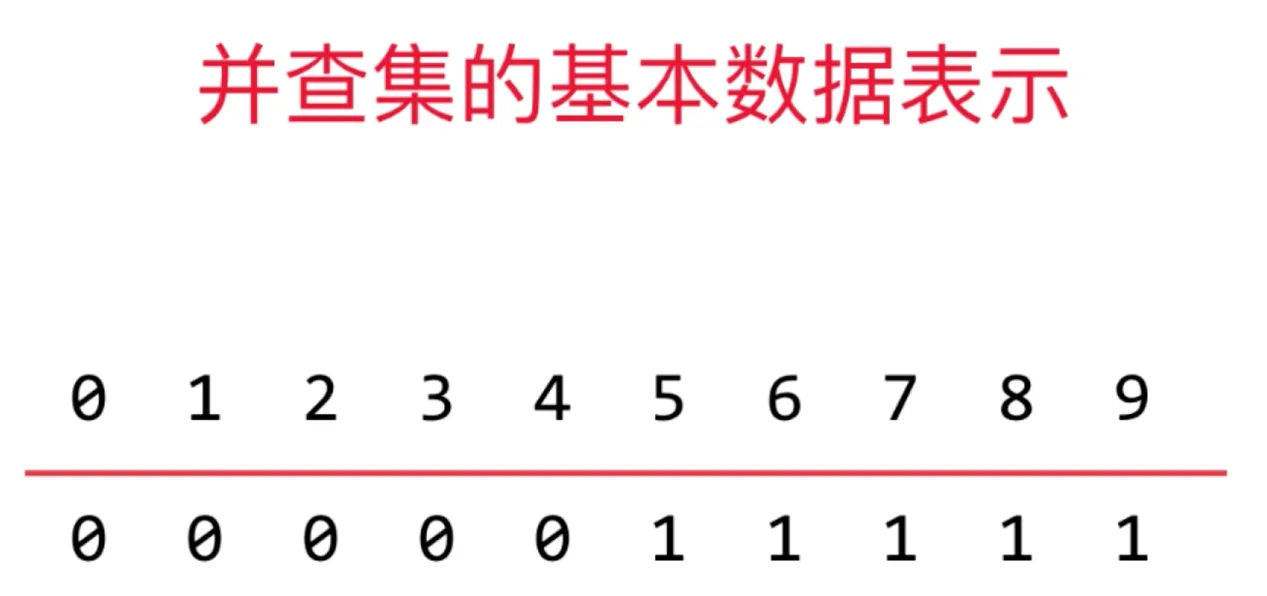 上图 0-4 属于一个集合,5-9属于另一个集合
编号 0 和 编号 1 也就是可连接的
上图 0-4 属于一个集合,5-9属于另一个集合
编号 0 和 编号 1 也就是可连接的

并查集需要实现的接口
// 查看元素 p 和元素 q 是否属于同一个集合
boolean isConnected(int p, int q);
// 把 p 和 q 所在的集合连接起来
void unionElements(int p, int q);使用数组实现,数组存储节点所在的集合编号 那么,isConnected 通过下标比较集合编号即可,复杂度是 O(1) unionElements 需要遍历整个数组,把 p 所在的下标改为 q,复杂度是 O(n)
把每一个元素看作是节点,
在一个集合中,节点 3 指向 节点 2, 节点 2 作为树的根节点,指向自己
向这个集合添加元素,指向根节点即可
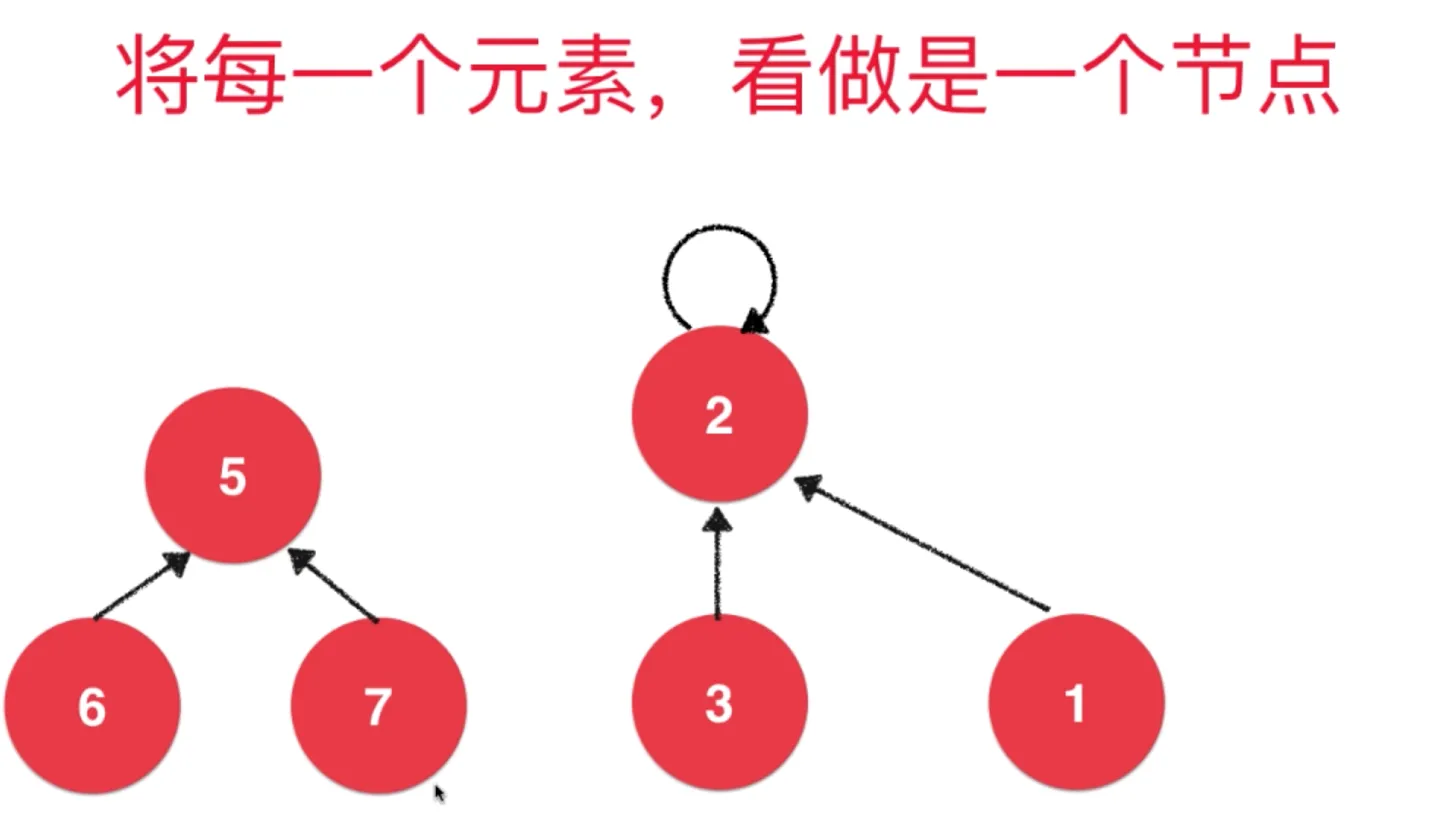 合并两个集合,把集合根节点,指向另一个集合的根节点
合并两个集合,把集合根节点,指向另一个集合的根节点
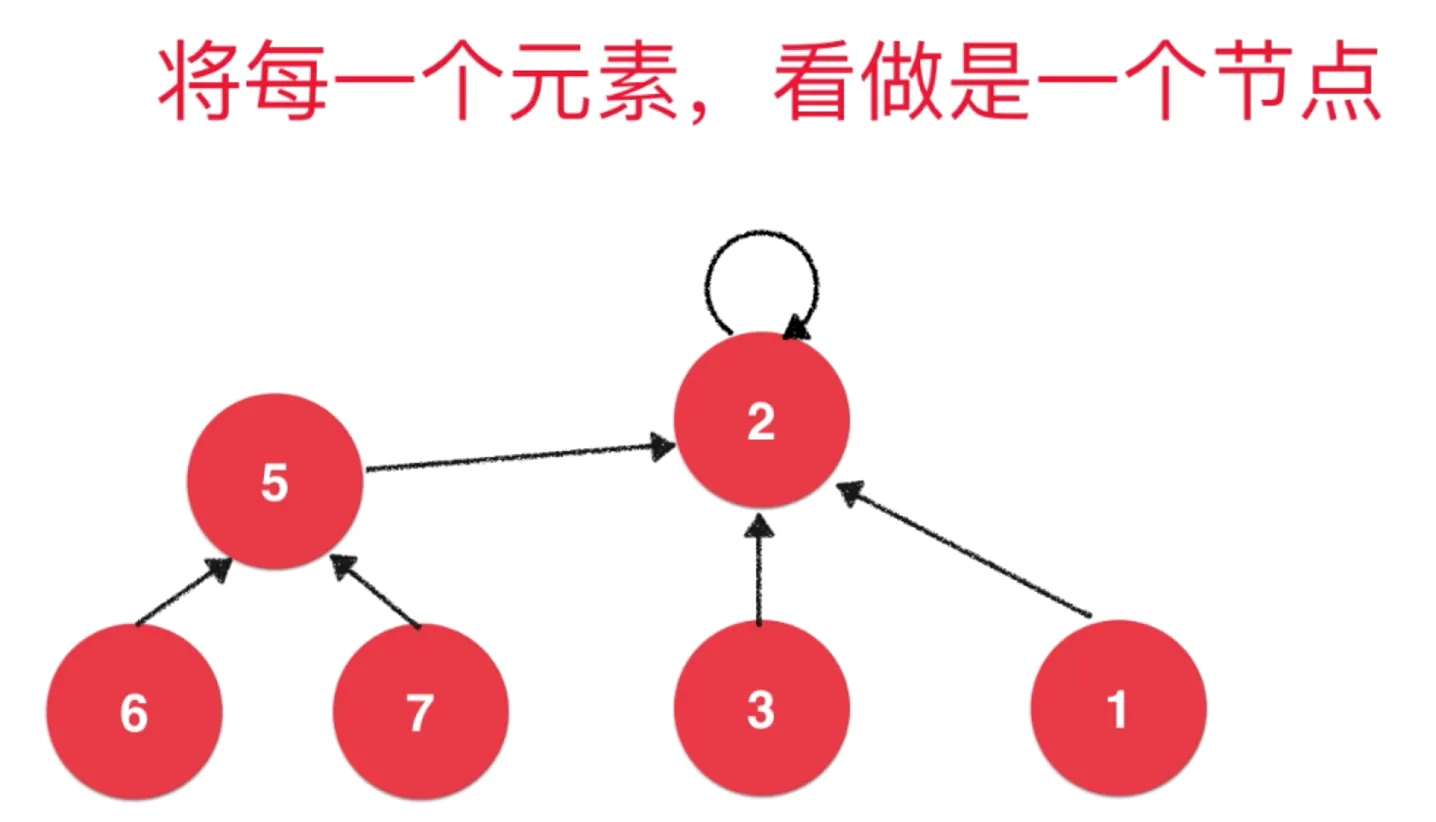
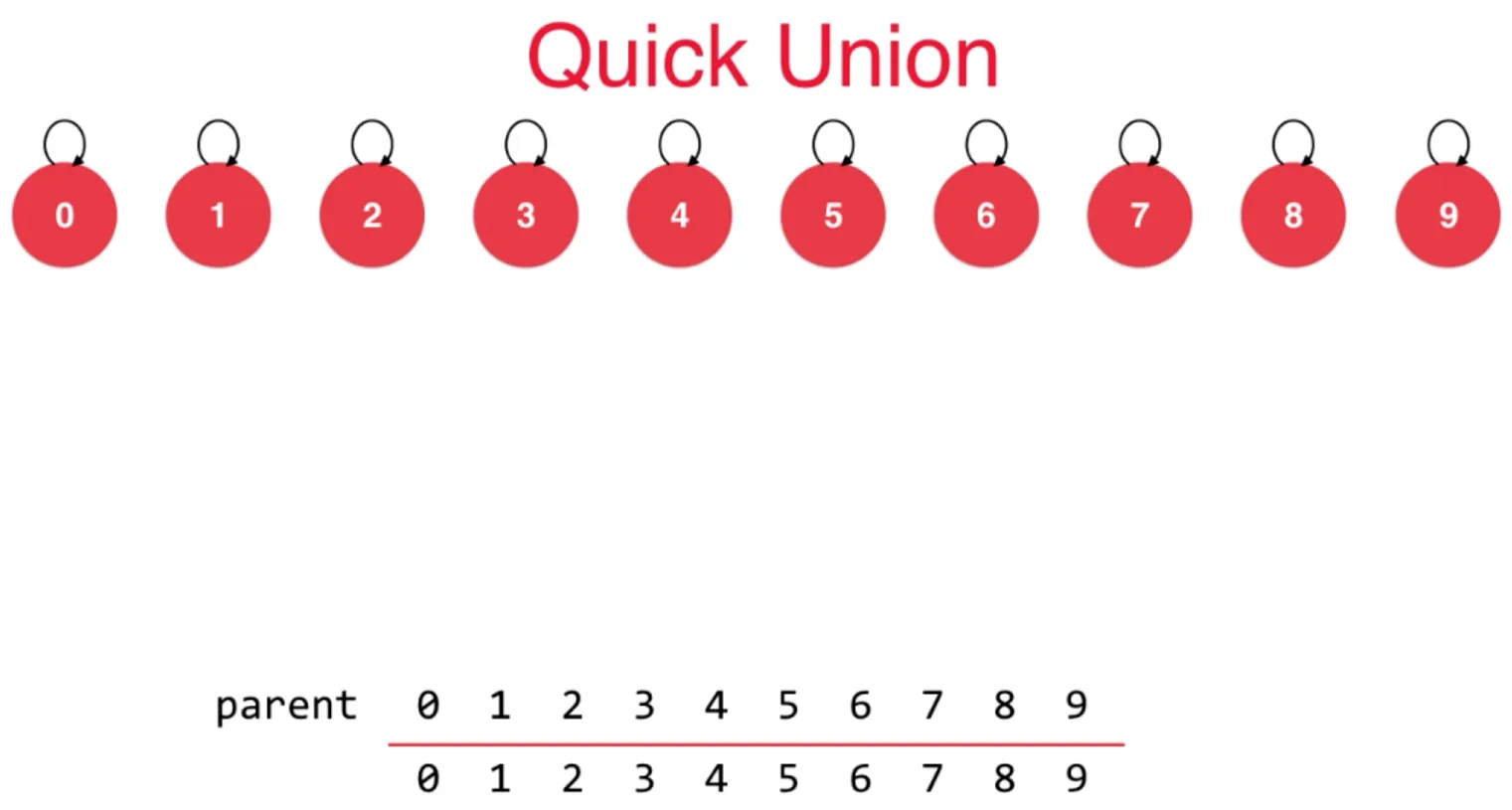
在数组中,初始时候,每个元素指向它的父节点
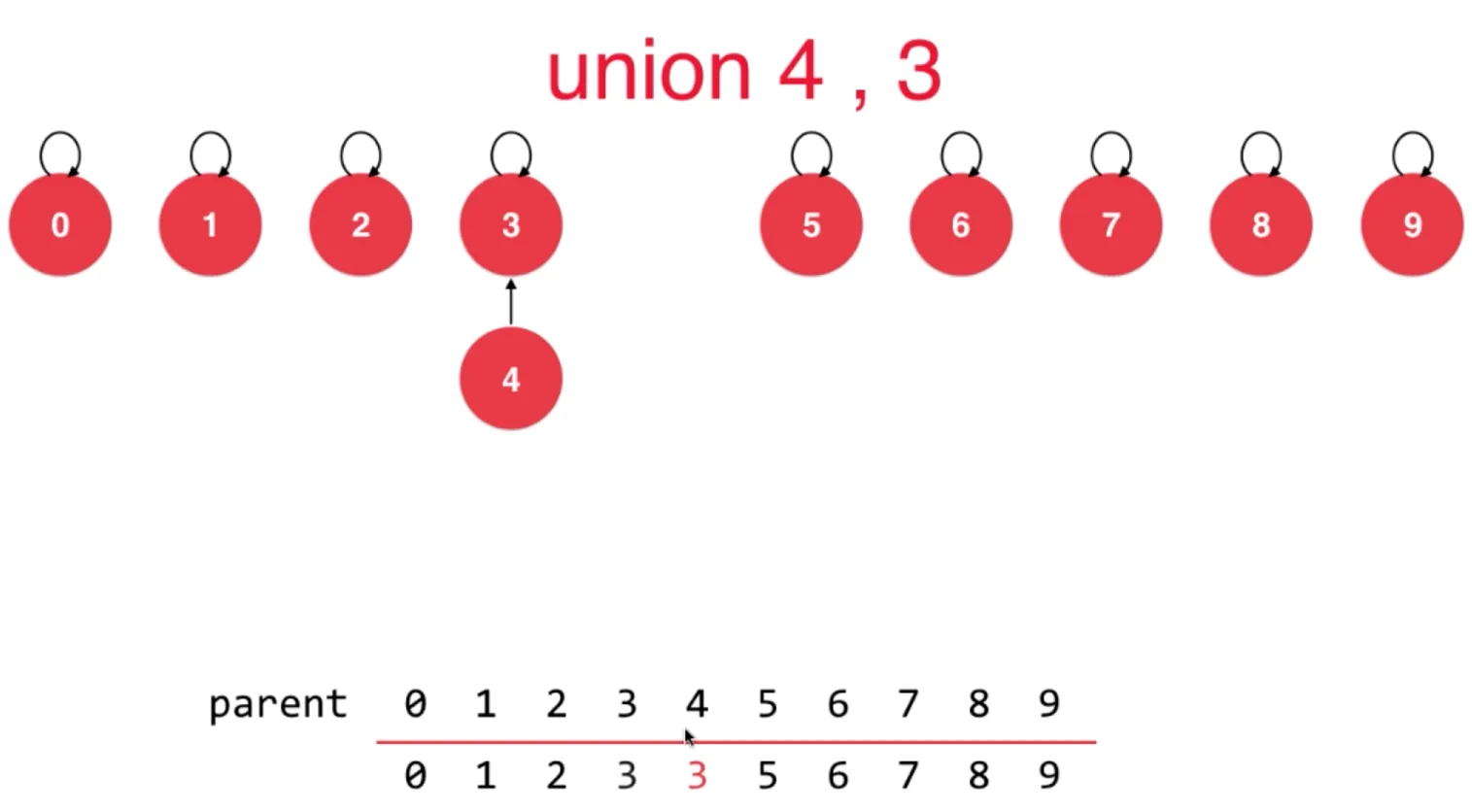
 Union(4, 3), 让节点 4 指向节点 3,在数组中,把 4 所在位置值修改为 3 存储的值
Union(4, 3), 让节点 4 指向节点 3,在数组中,把 4 所在位置值修改为 3 存储的值
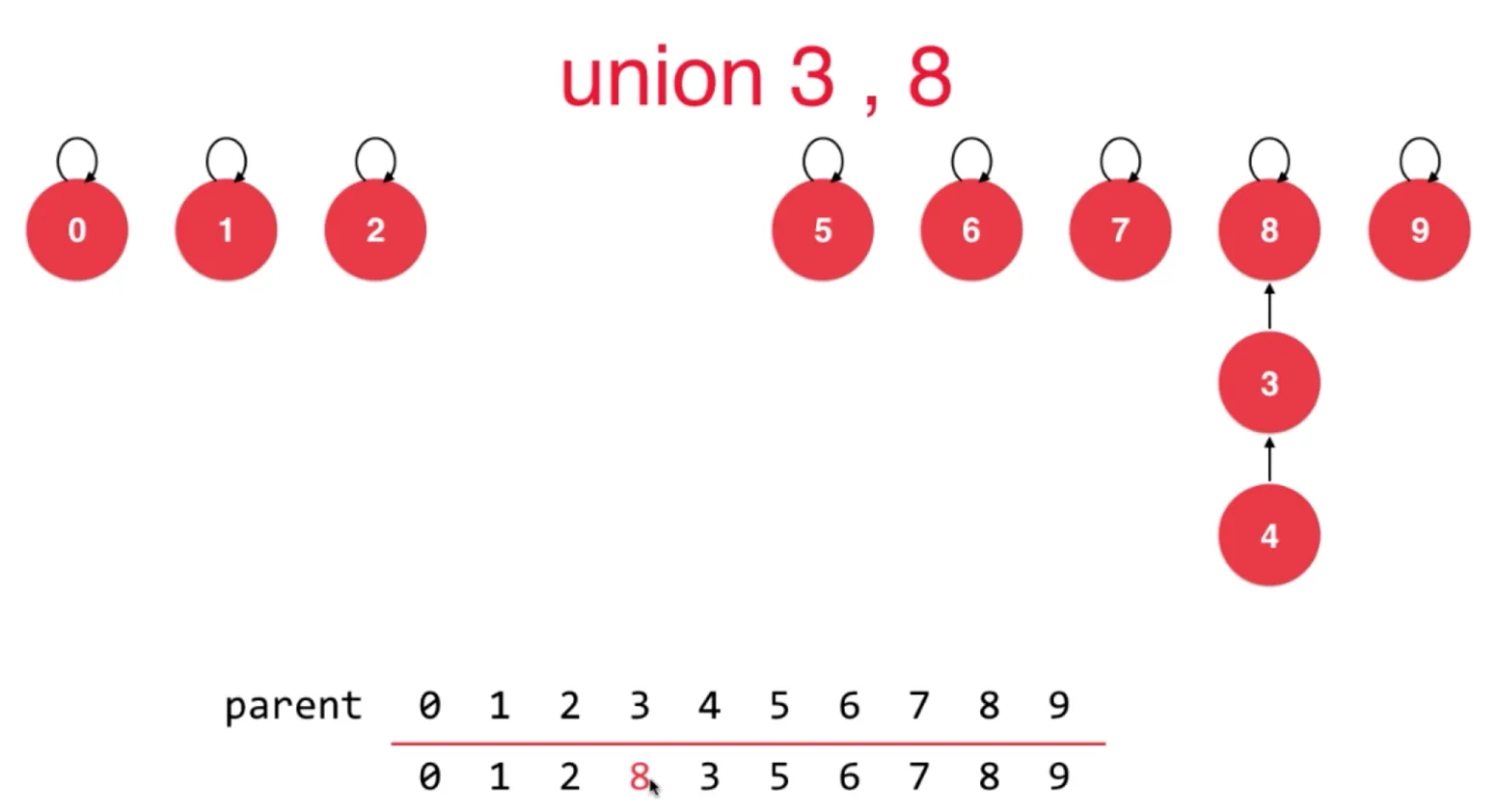
 Union(3, 8)
Union(3, 8)
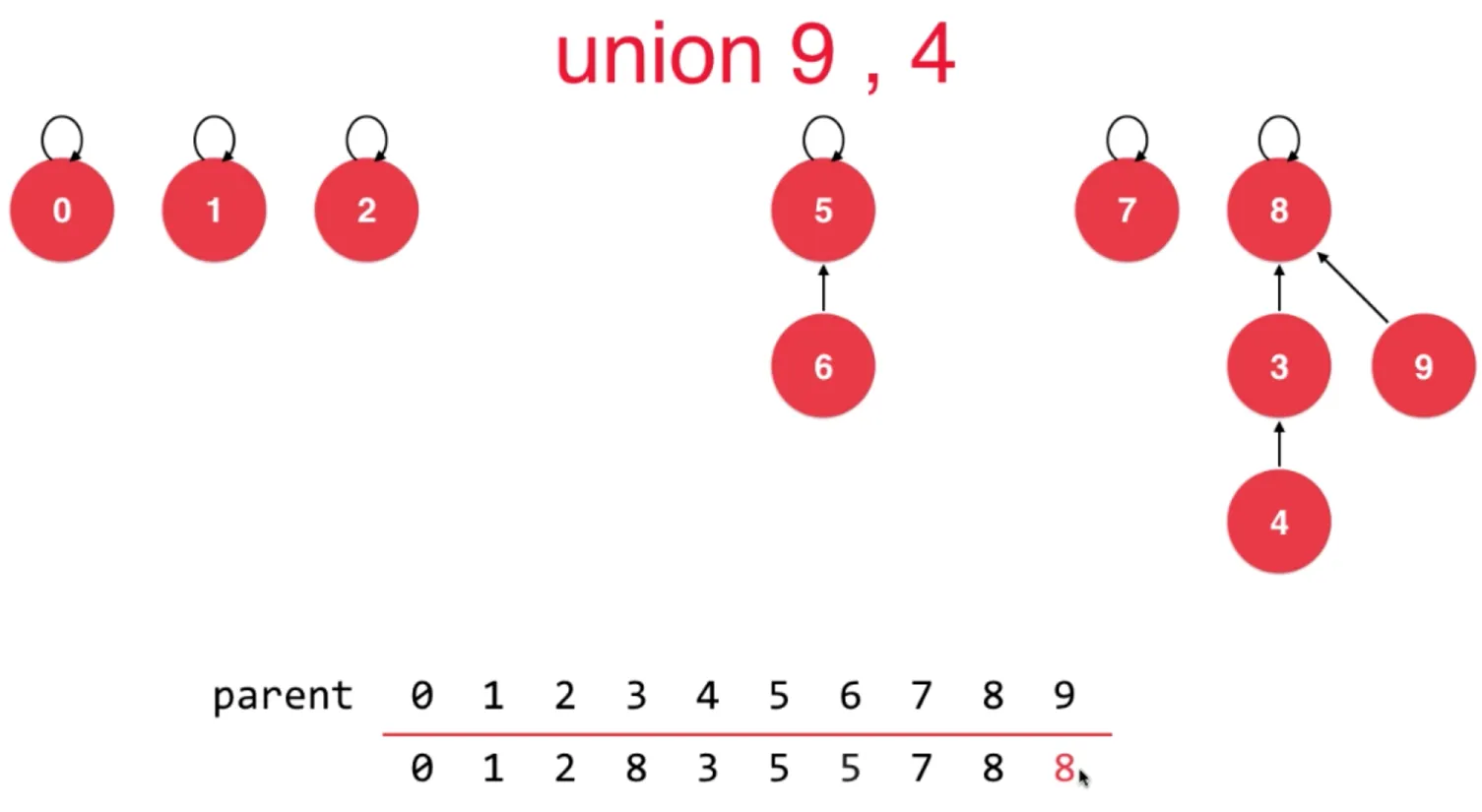
基于 size 的优化
如果我们在合并时,单纯让 p 所在根节点指向 q 所在根节点, 那么极端情况下有可能会形成链表 优化思路:记录每个节点的树的节点数量,当合并时判断,把节点少的合并到节点多的树上
UnionFind1: 3.782069081 s UnionFind2: 5.547484642 s UnionFind3: 0.009774763 s
基于 rank 的优化
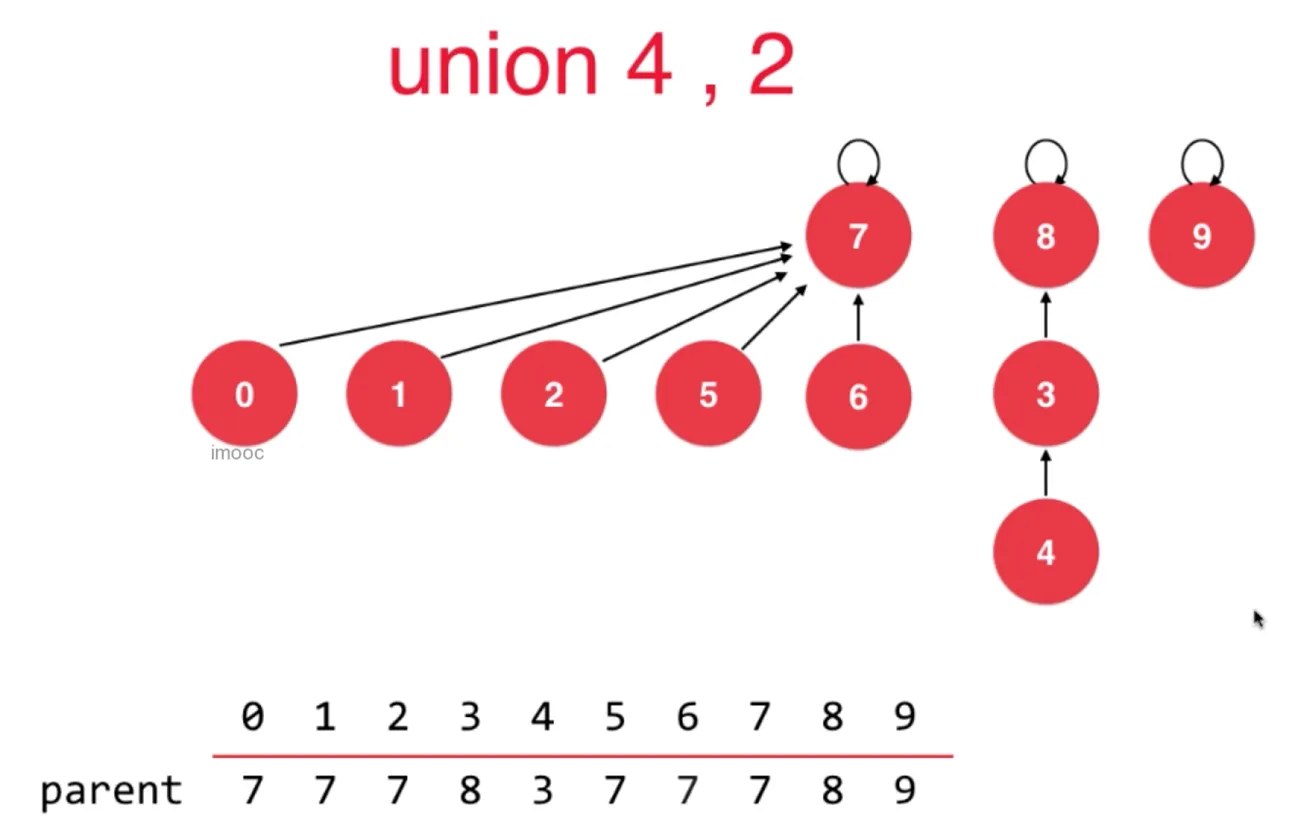 如果基于 size 优化,合并后,节点 8 指向 节点多的根节点 7
如果基于 size 优化,合并后,节点 8 指向 节点多的根节点 7
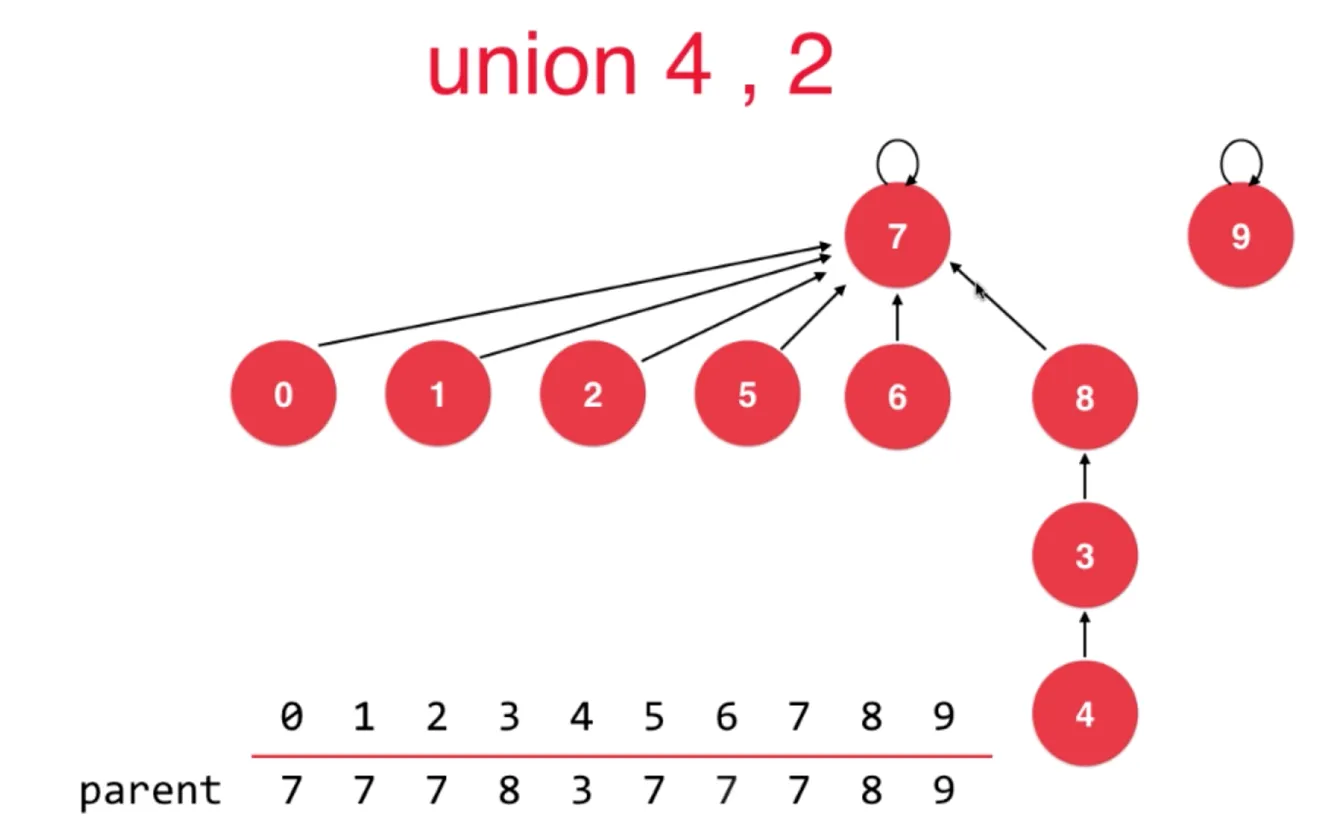 此时树的深度为 4,更合理的合并应该是让 节点7指向节点 8
此时树的深度为 4,更合理的合并应该是让 节点7指向节点 8
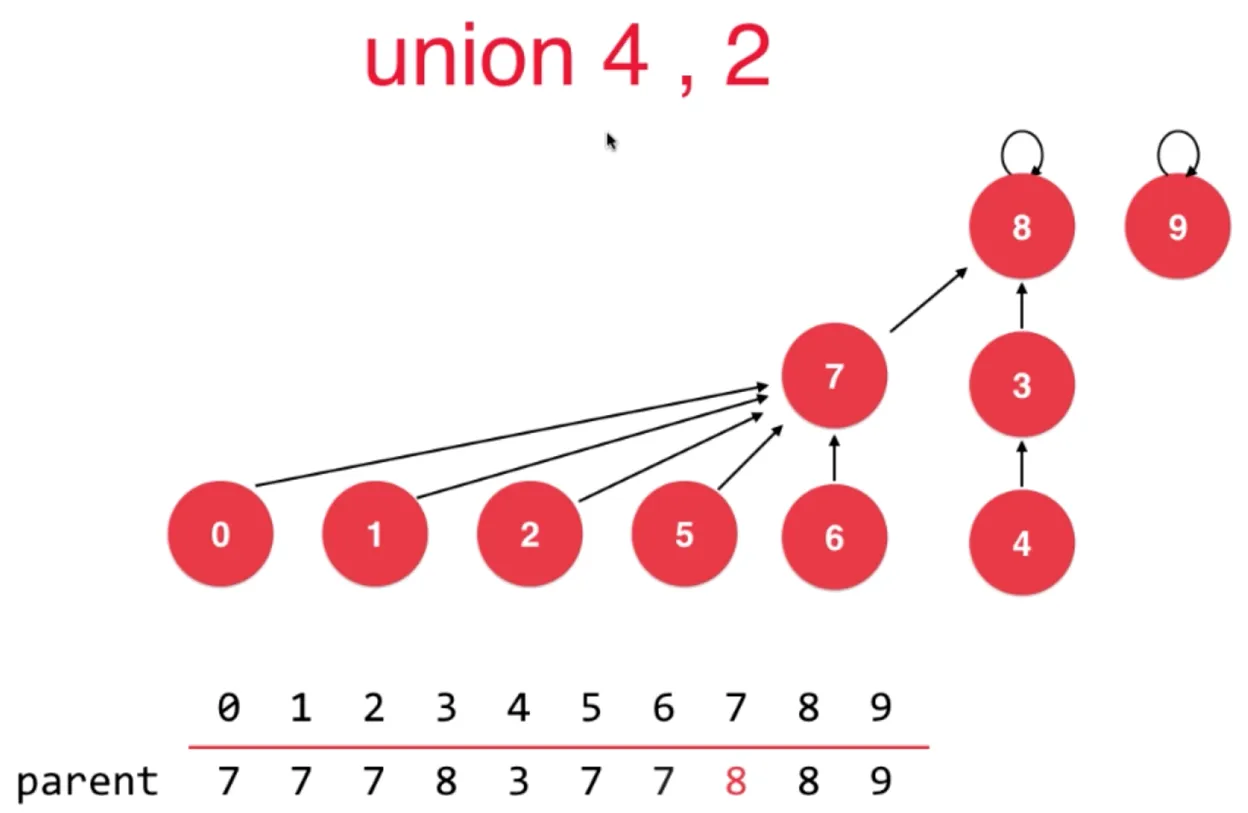
rank[i] 表示根节点为 i 的树的高度
路径压缩
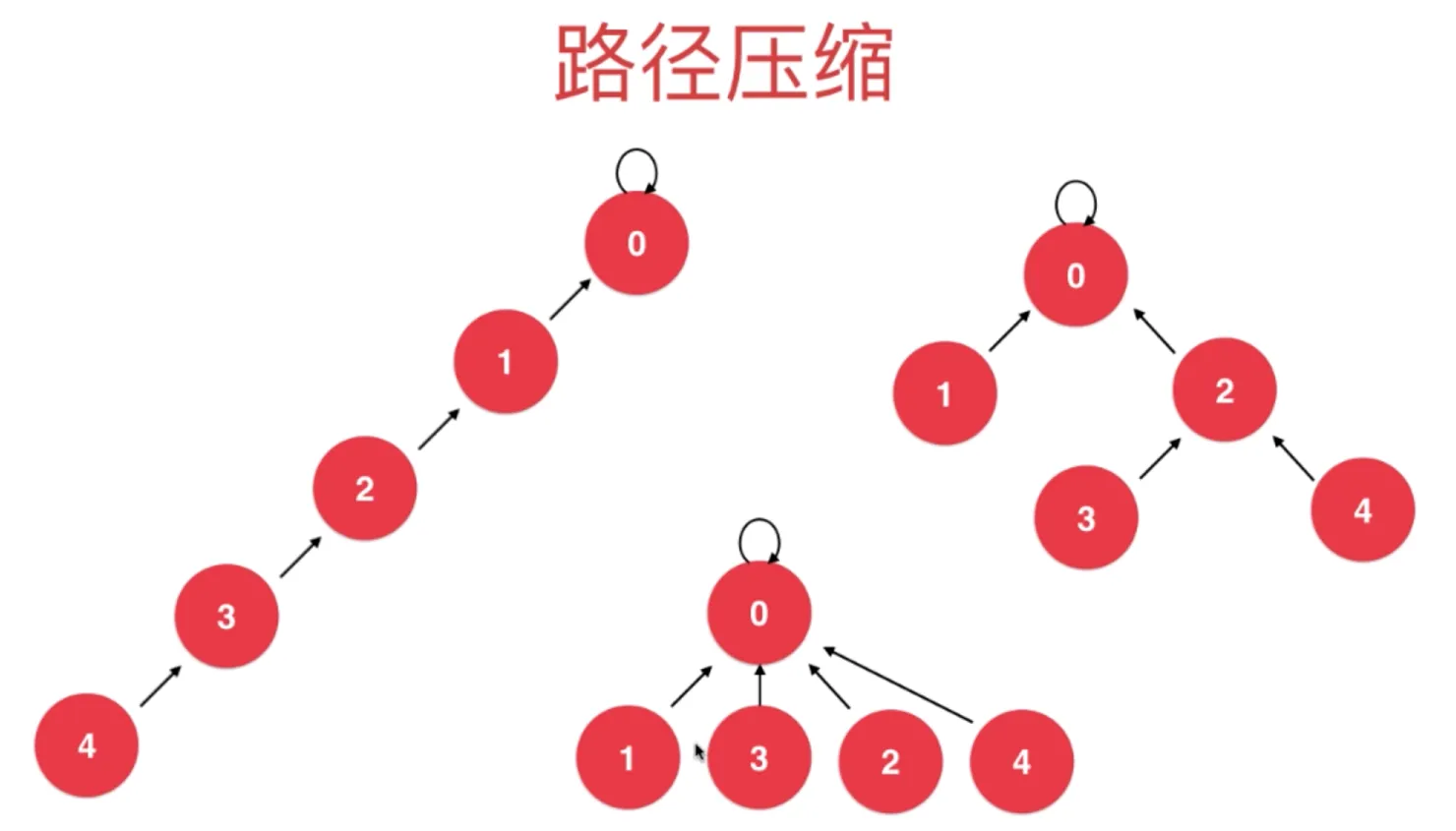
执行 find 时候进行压缩
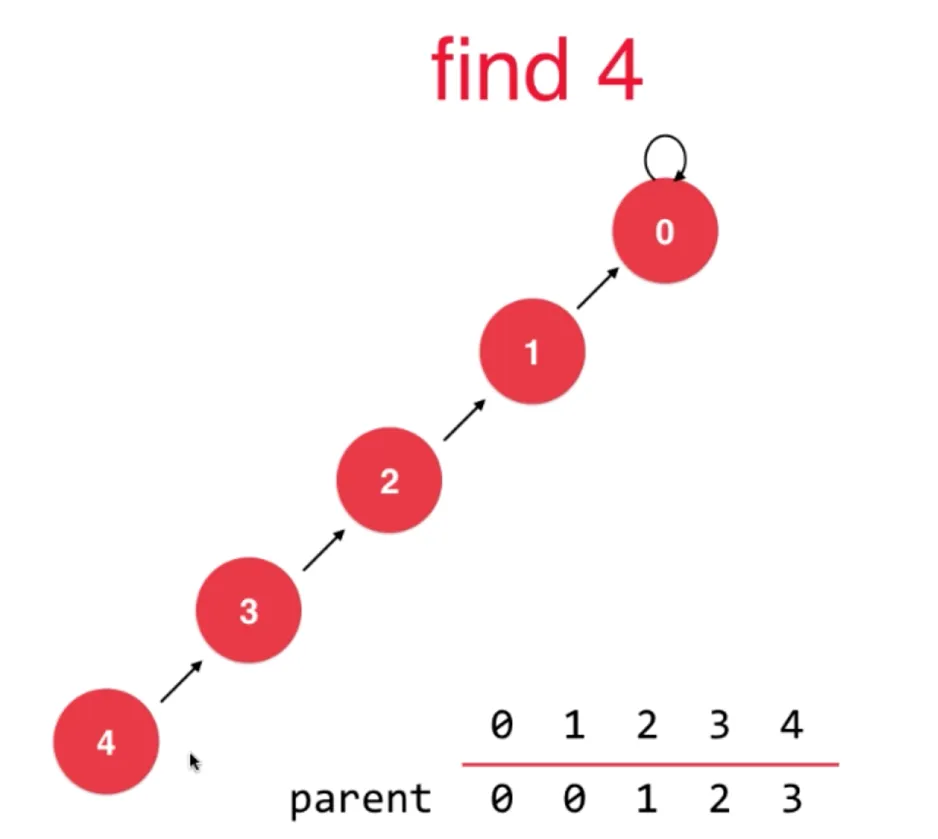 遍历过程中执行
遍历过程中执行 parent[p] = parent[parent[p]],
把当前节点,指向它父节点的父节点
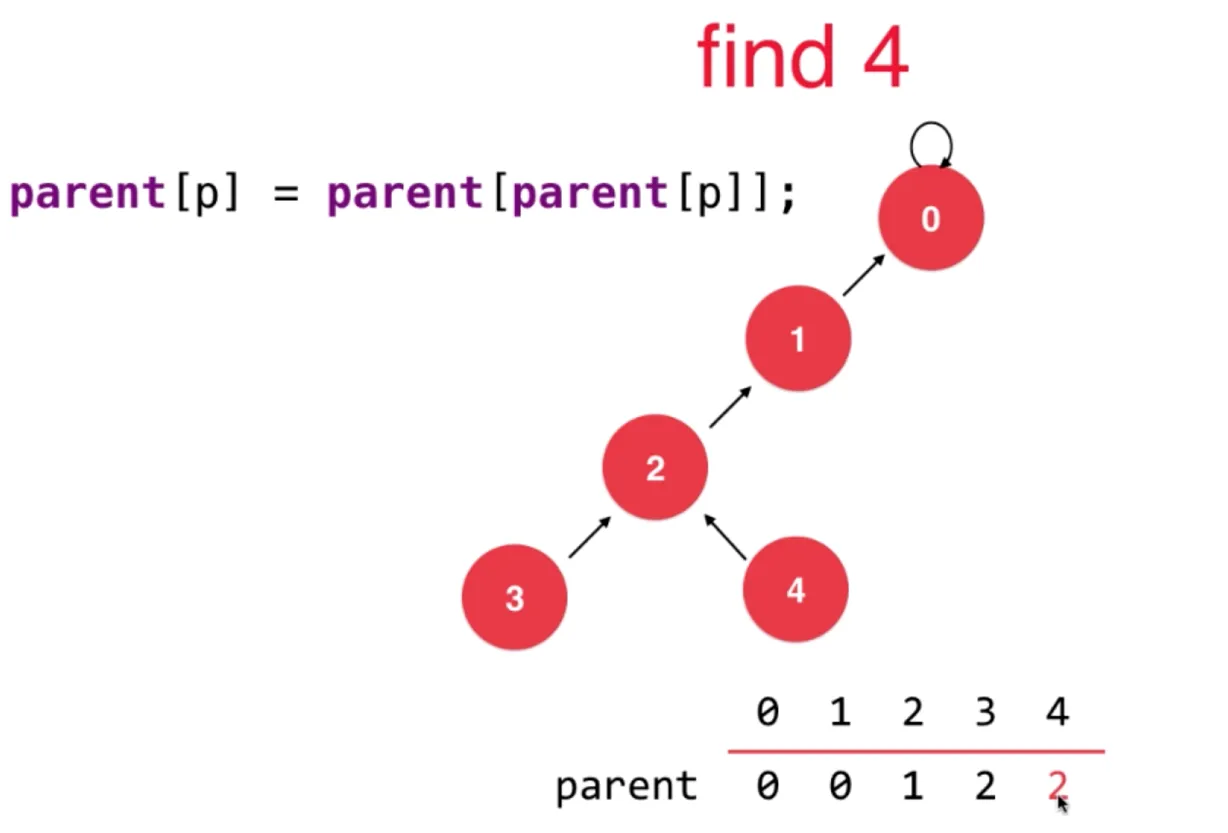
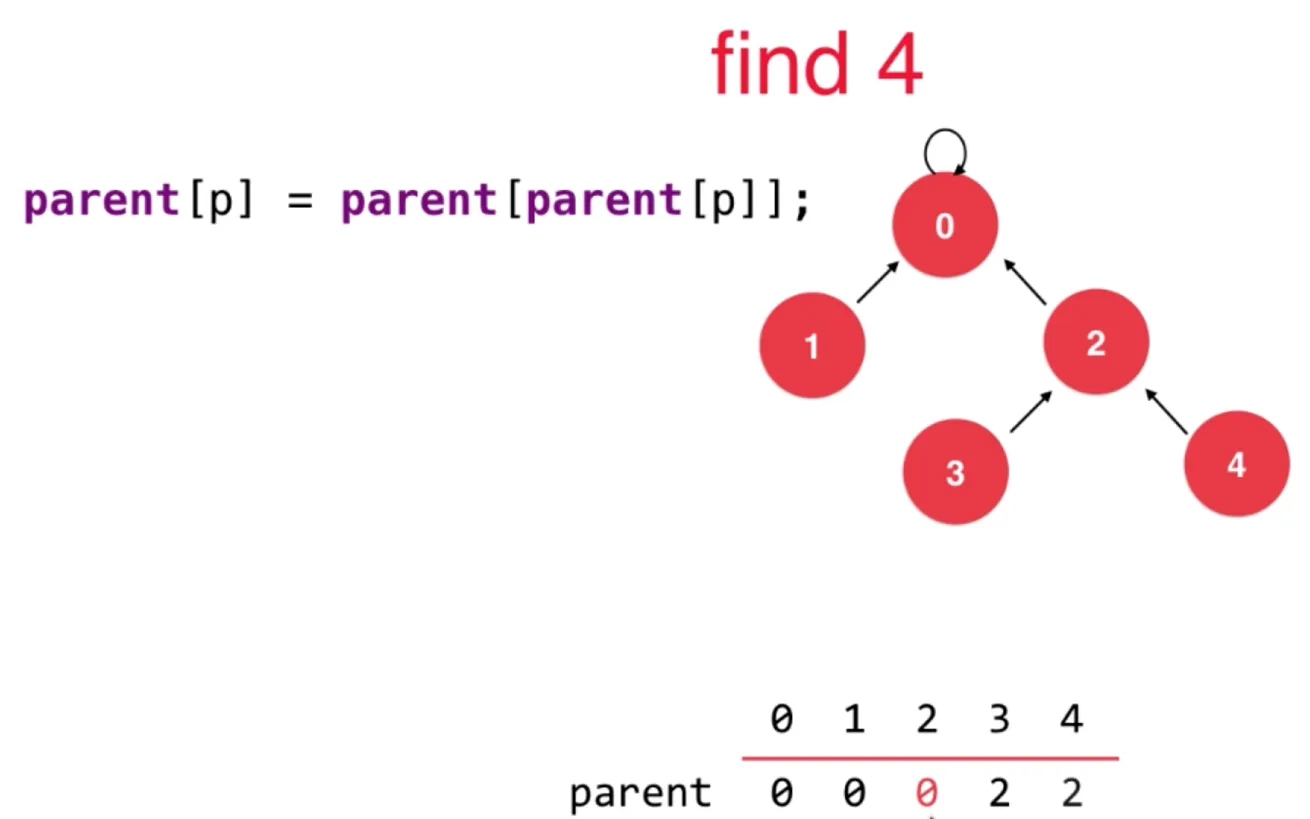
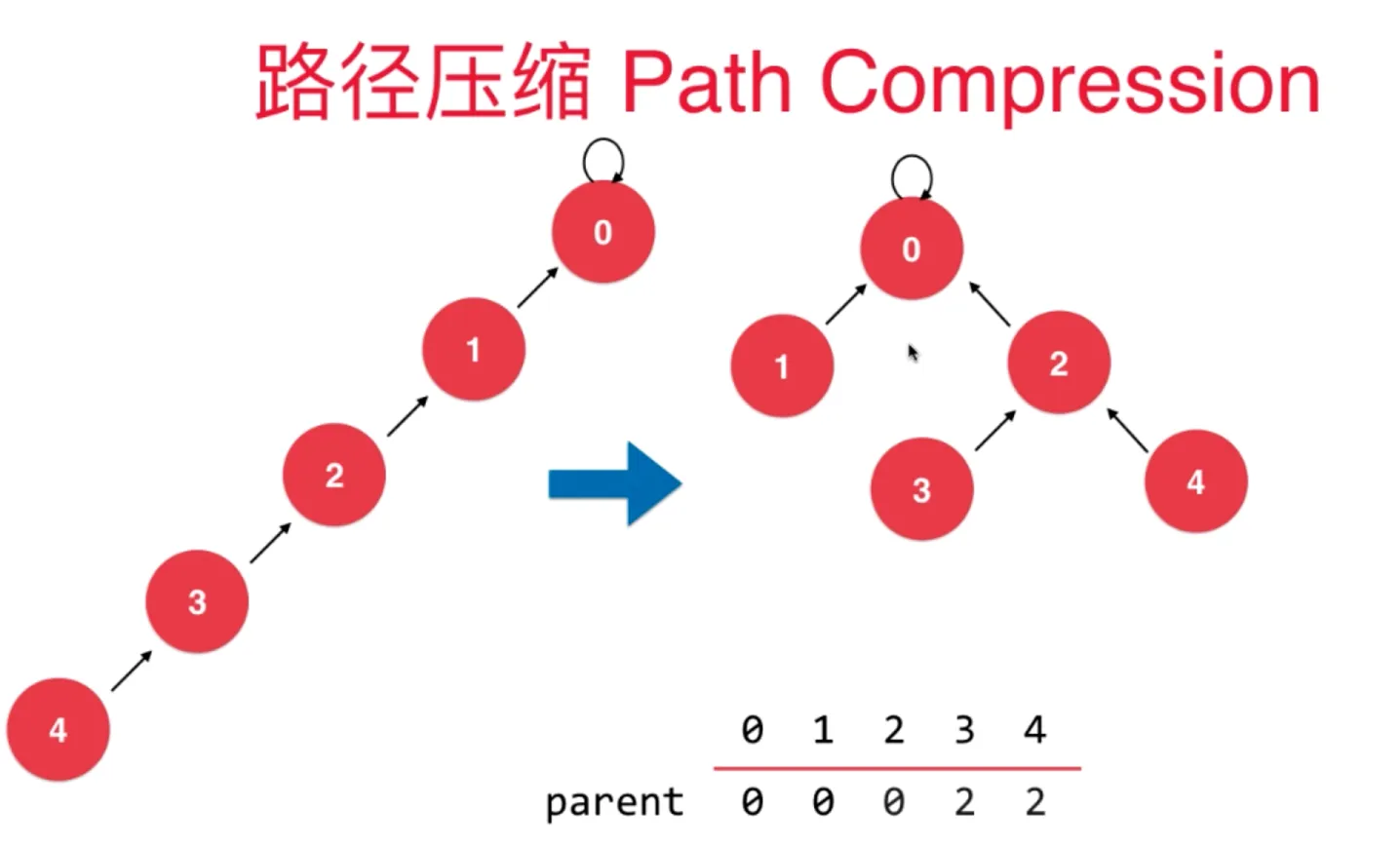
时间复杂度

AVL 树
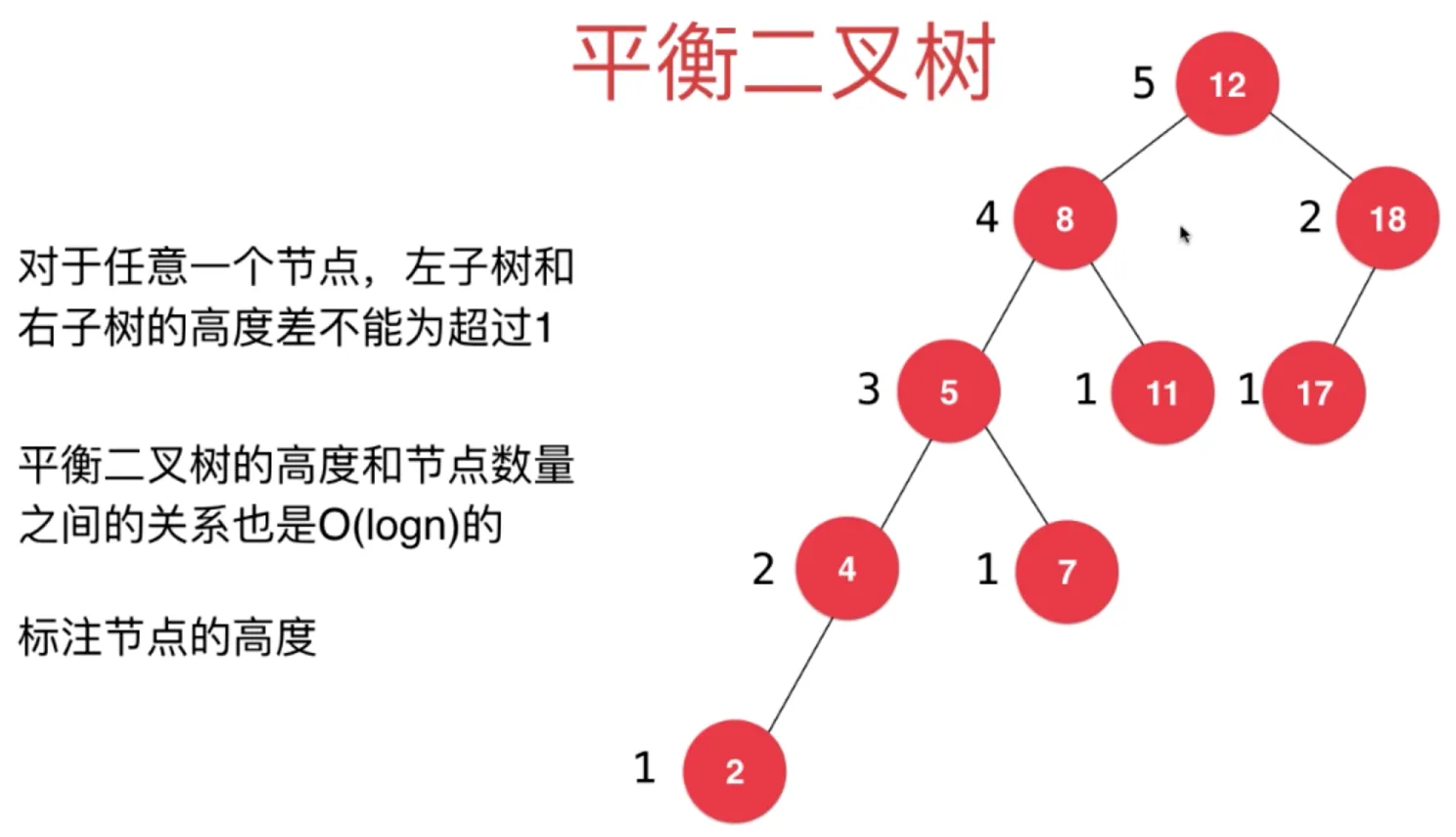
平衡二叉树:
对于任意一个节点,左子树和右子树的高度差不能超过 1
平衡二叉树的高度和节点数量之间的关系也是O(log(n))的
标注节点的高度 — 左右子树中最大高度加一
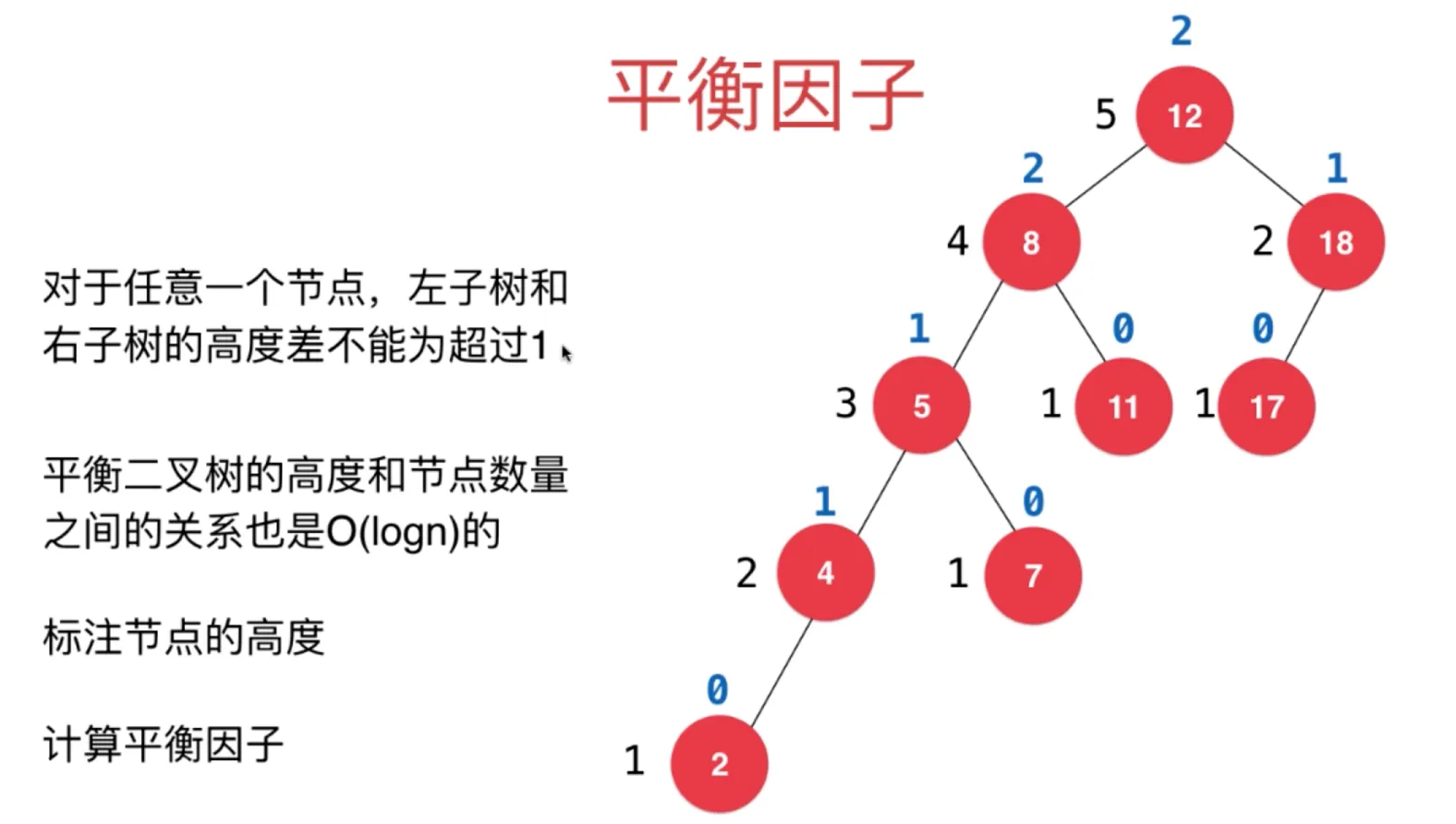
 计算平衡因子 — 左子树的高度减去右子树的高度
(如果平衡因子(高度差)大于等于 2,二叉树就不是平衡二叉树了)
计算平衡因子 — 左子树的高度减去右子树的高度
(如果平衡因子(高度差)大于等于 2,二叉树就不是平衡二叉树了)
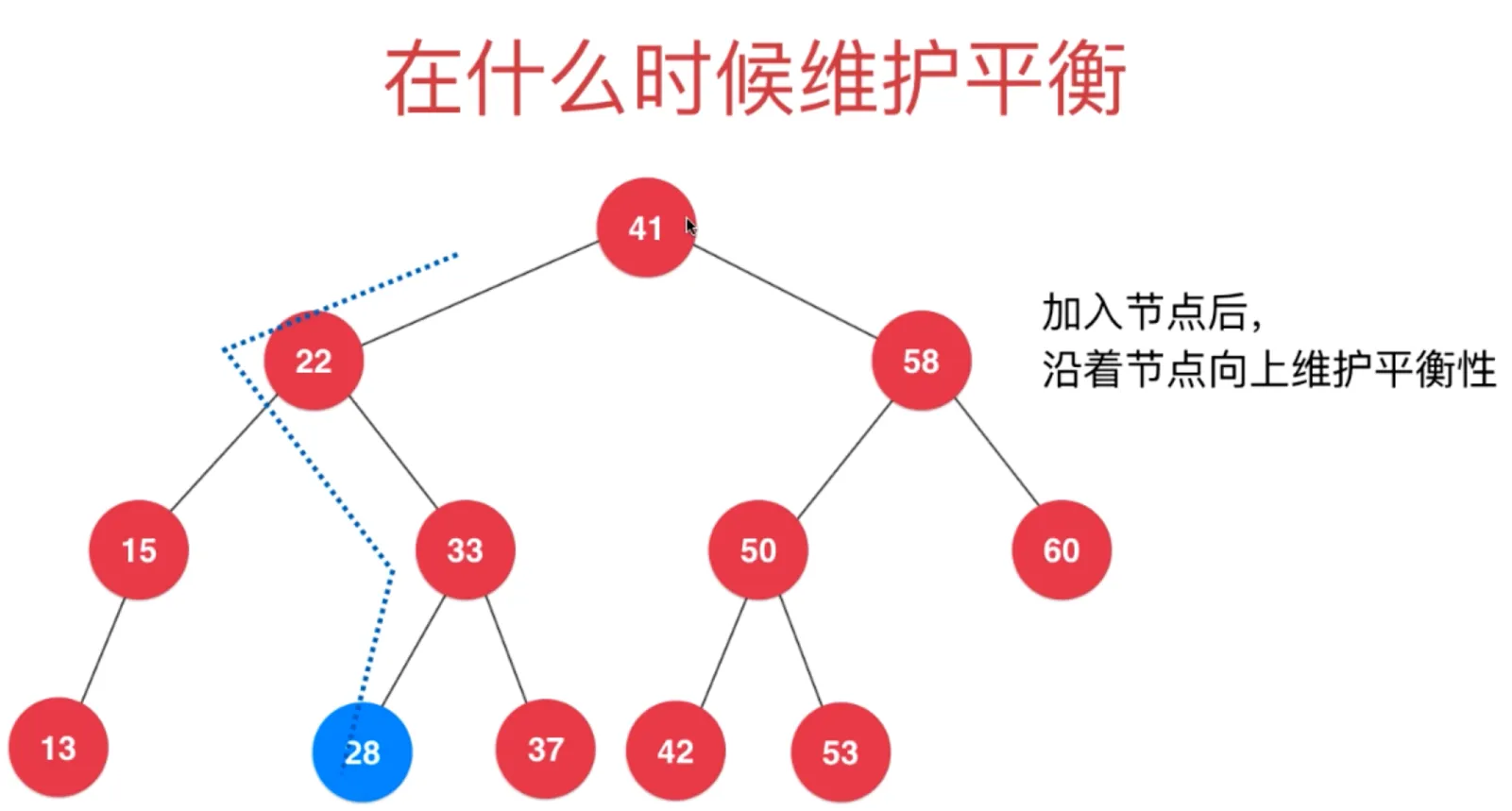
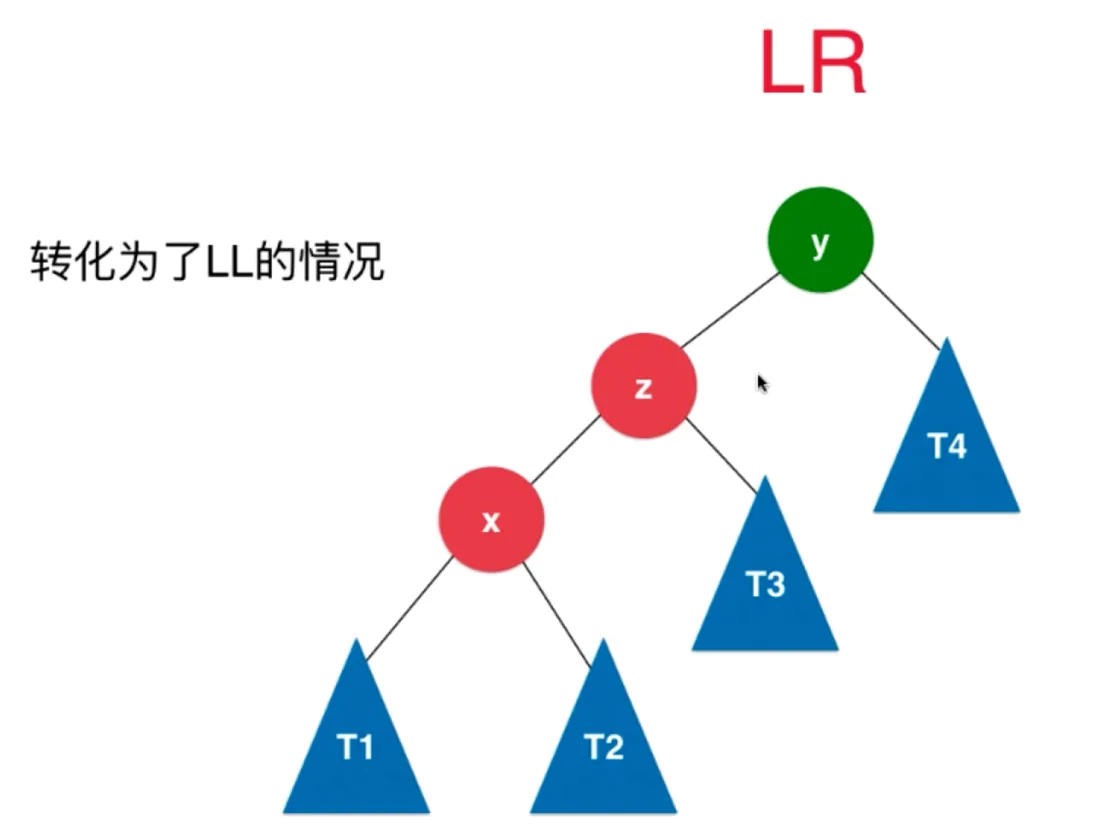
AVL 添加元素后,如何维持平衡
每添加一个节点,计算其父节点的平衡因子,判断是否打破平衡
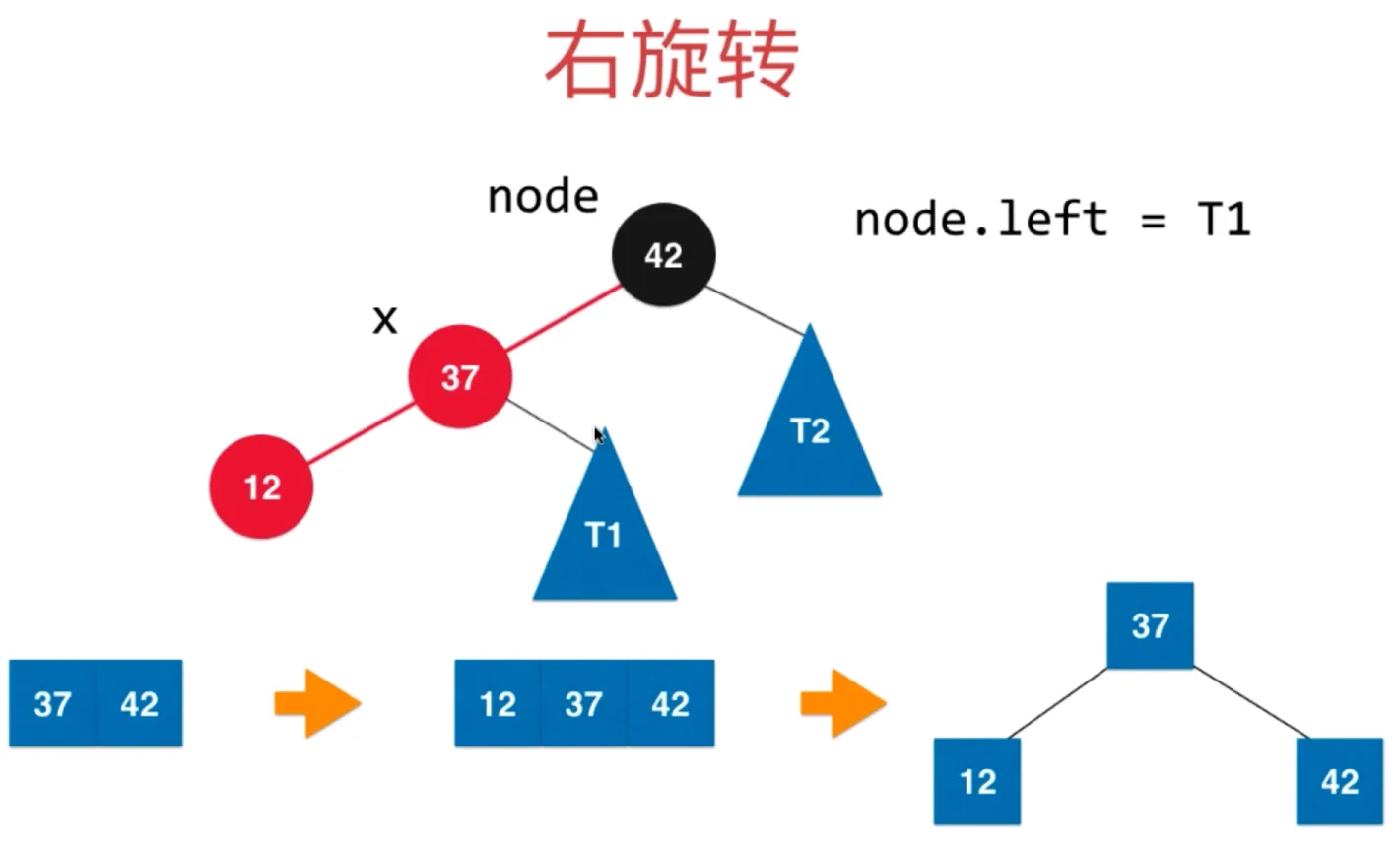
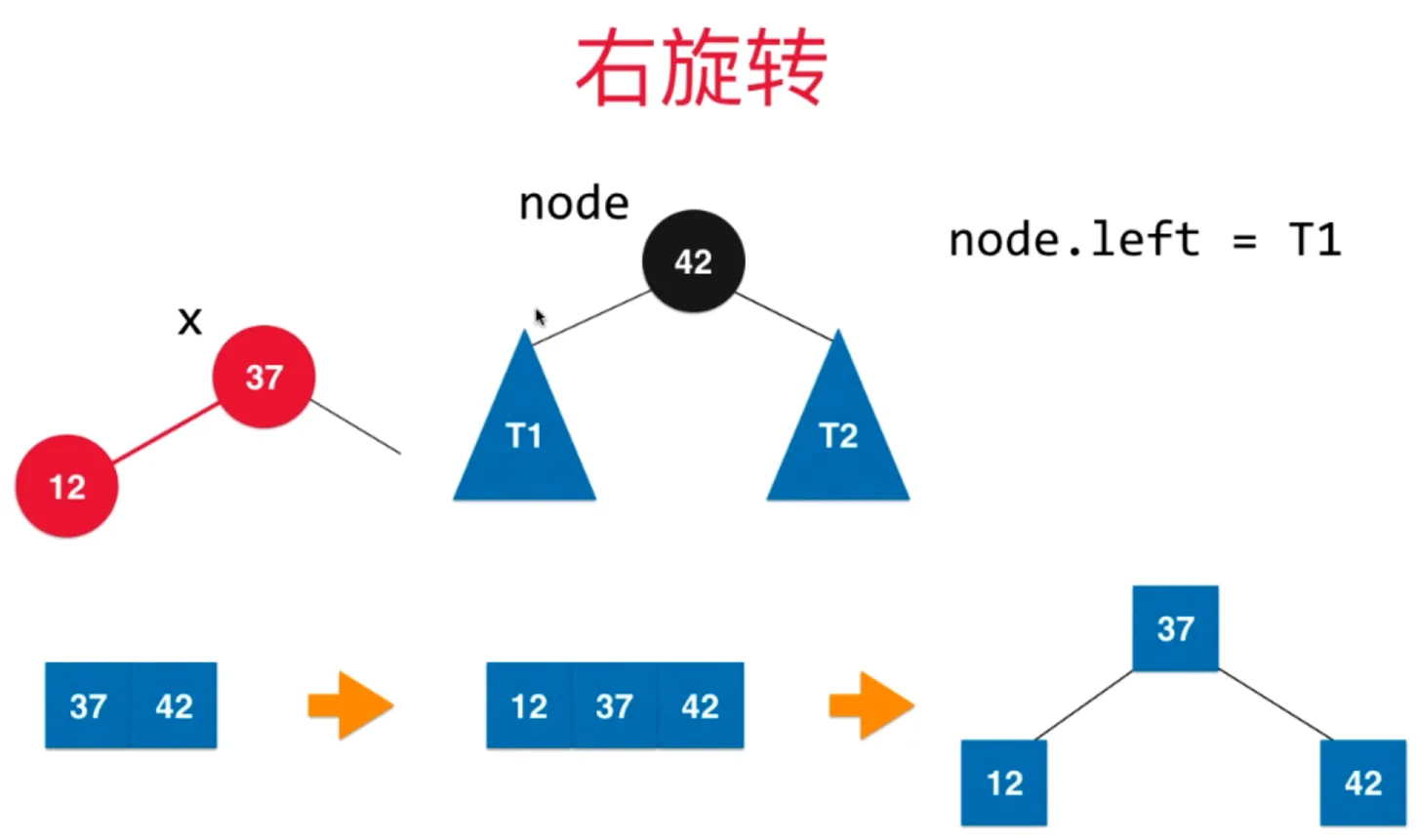
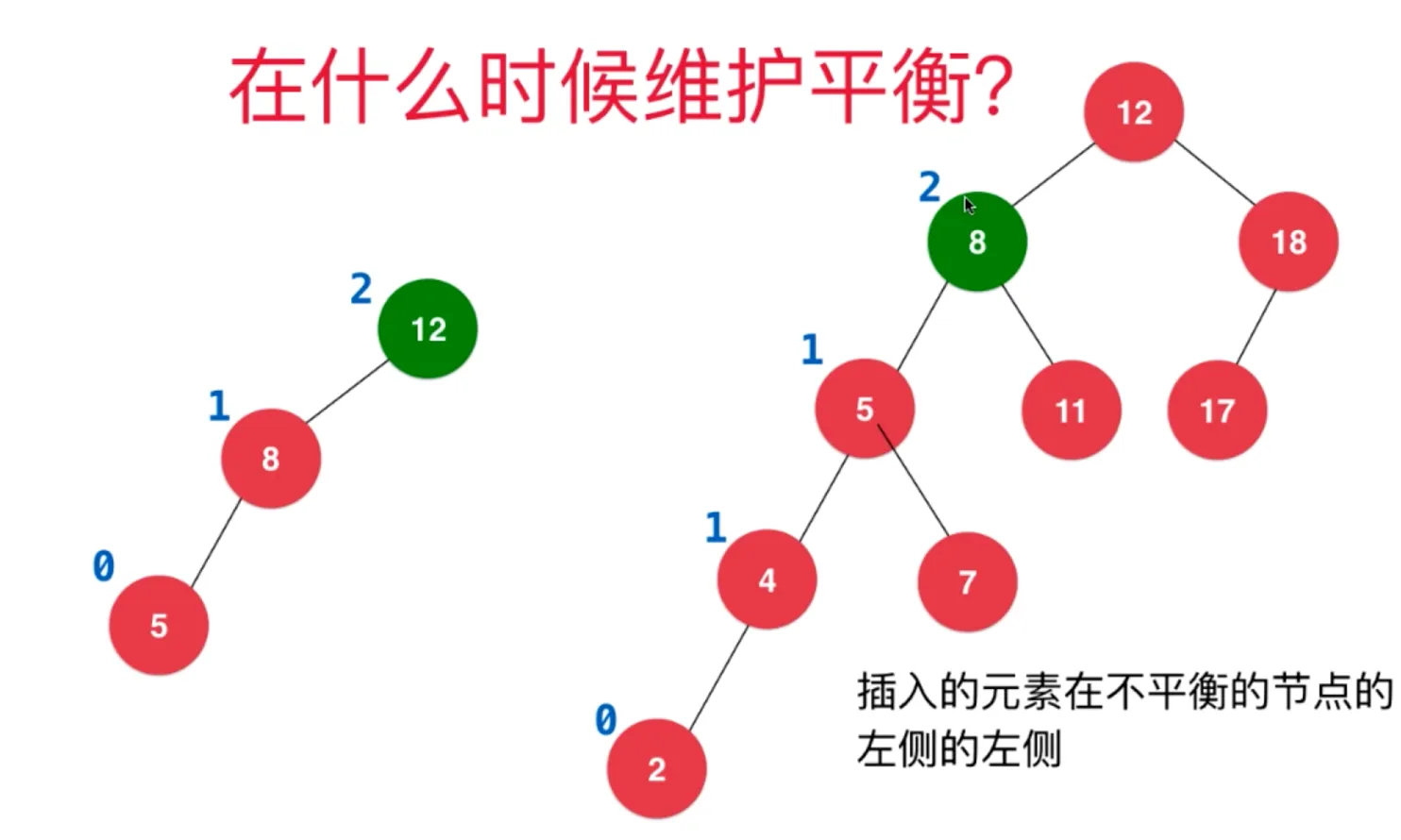 右旋转
右旋转
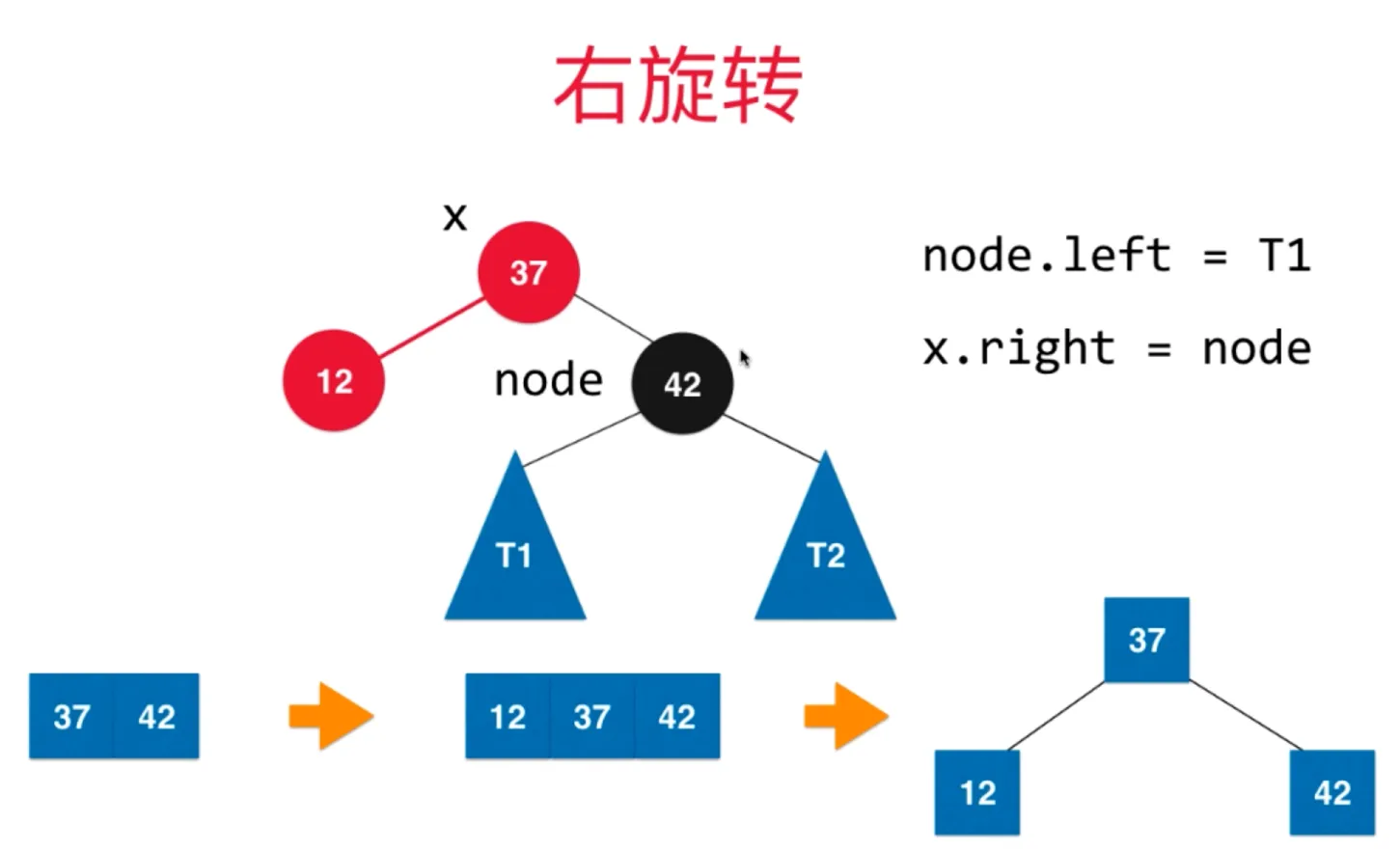
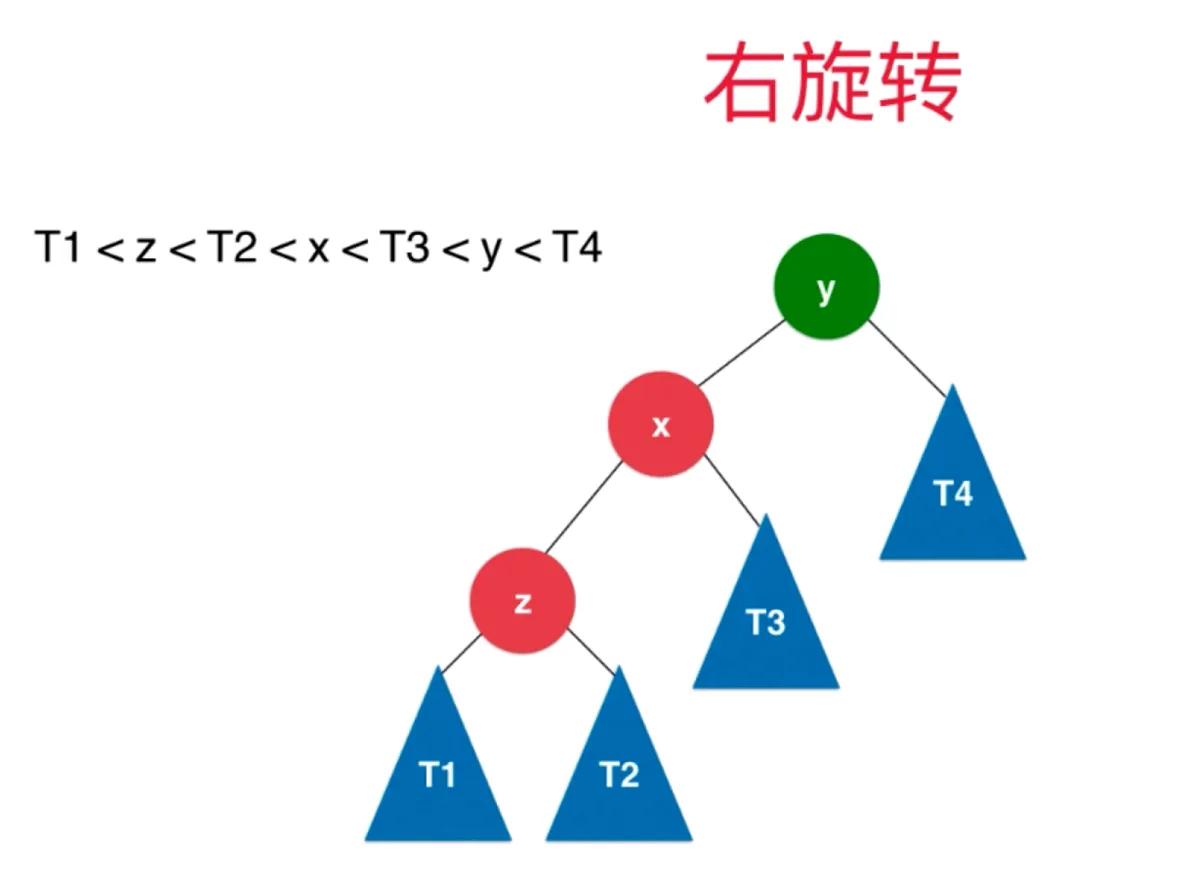 让 x 的右子树连接上 y (x.right = y)
让 x 的右子树连接上 y (x.right = y)
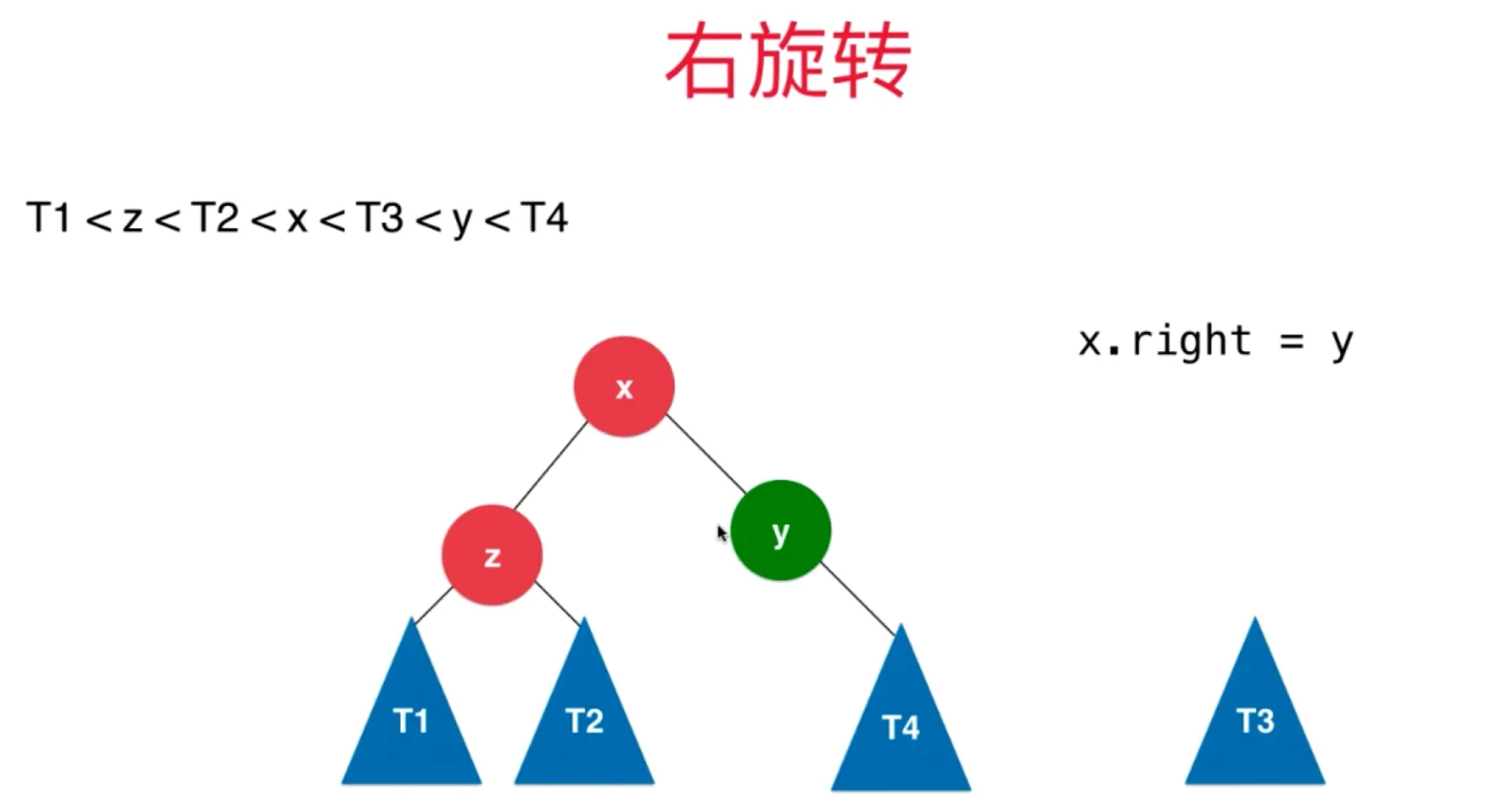 把 y 的左子树设置为 T3 (x.left = T3)
把 y 的左子树设置为 T3 (x.left = T3)
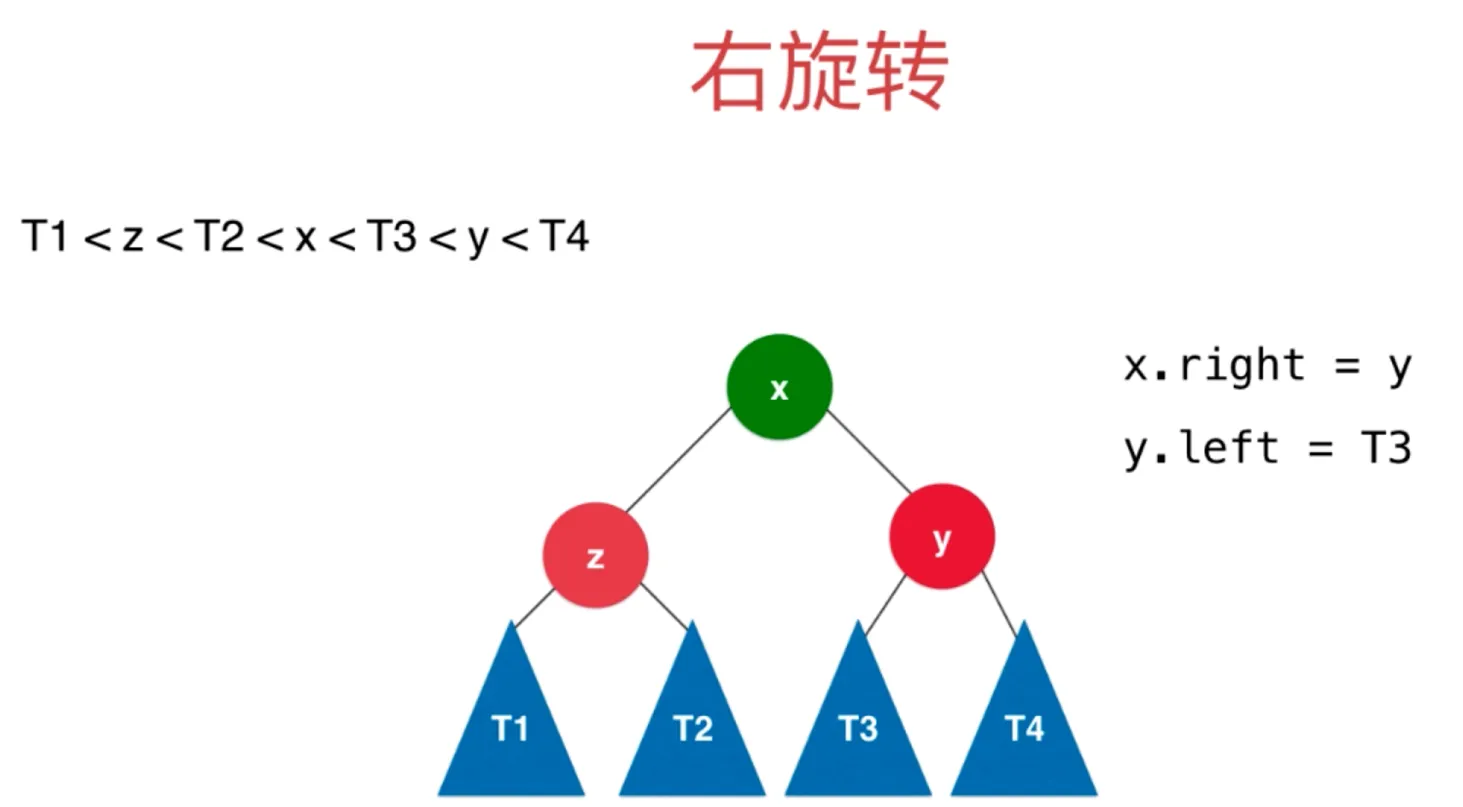 右旋转后的树满足平衡二叉树和二分搜索树的性质
右旋转后的树满足平衡二叉树和二分搜索树的性质
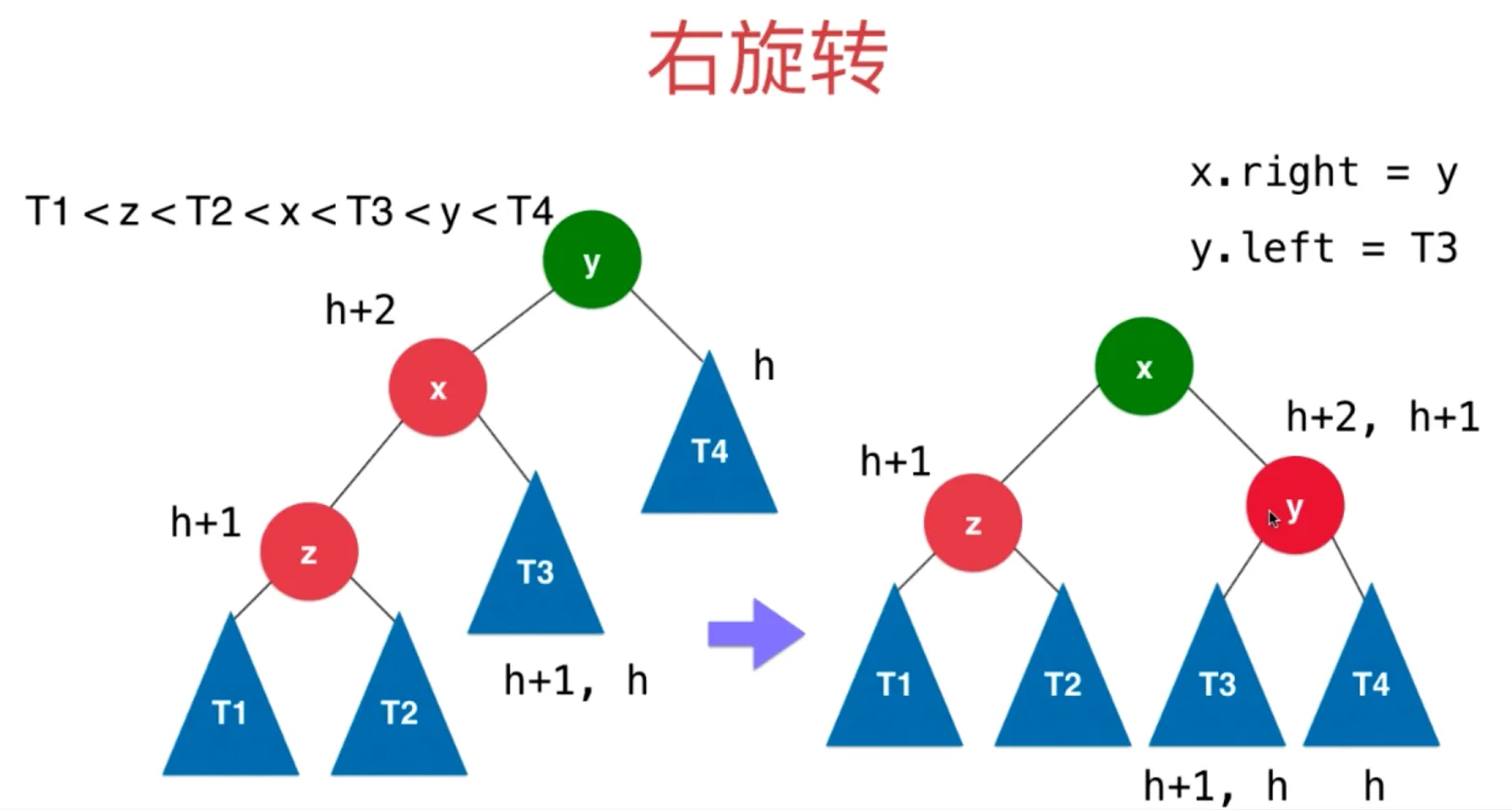
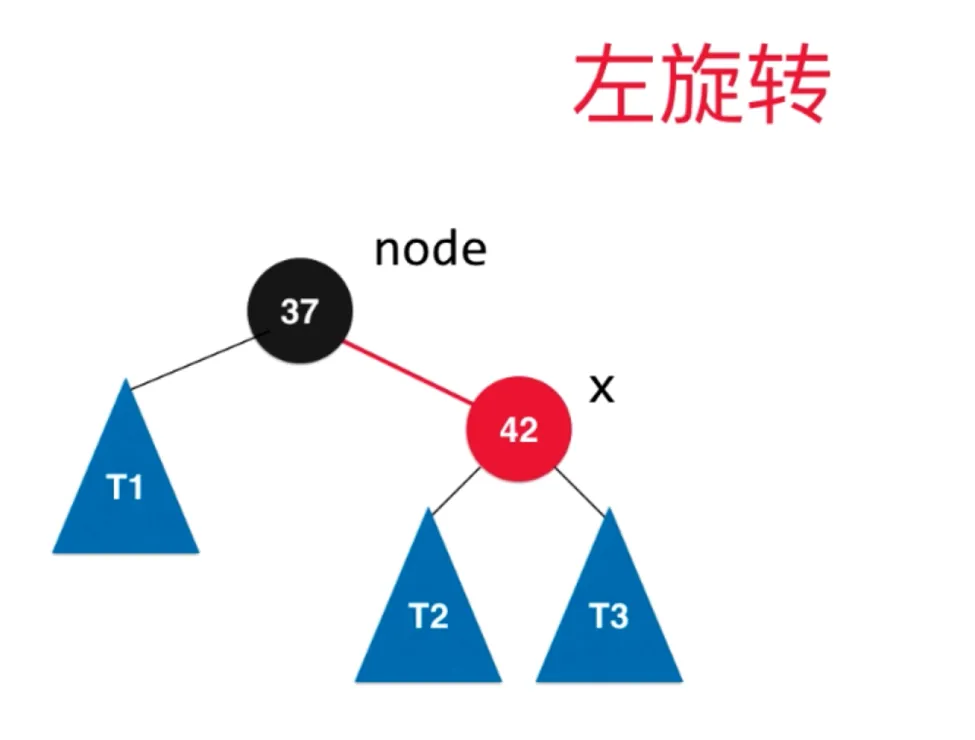
左旋转
插入的元素在不平衡的节点的右侧的右侧
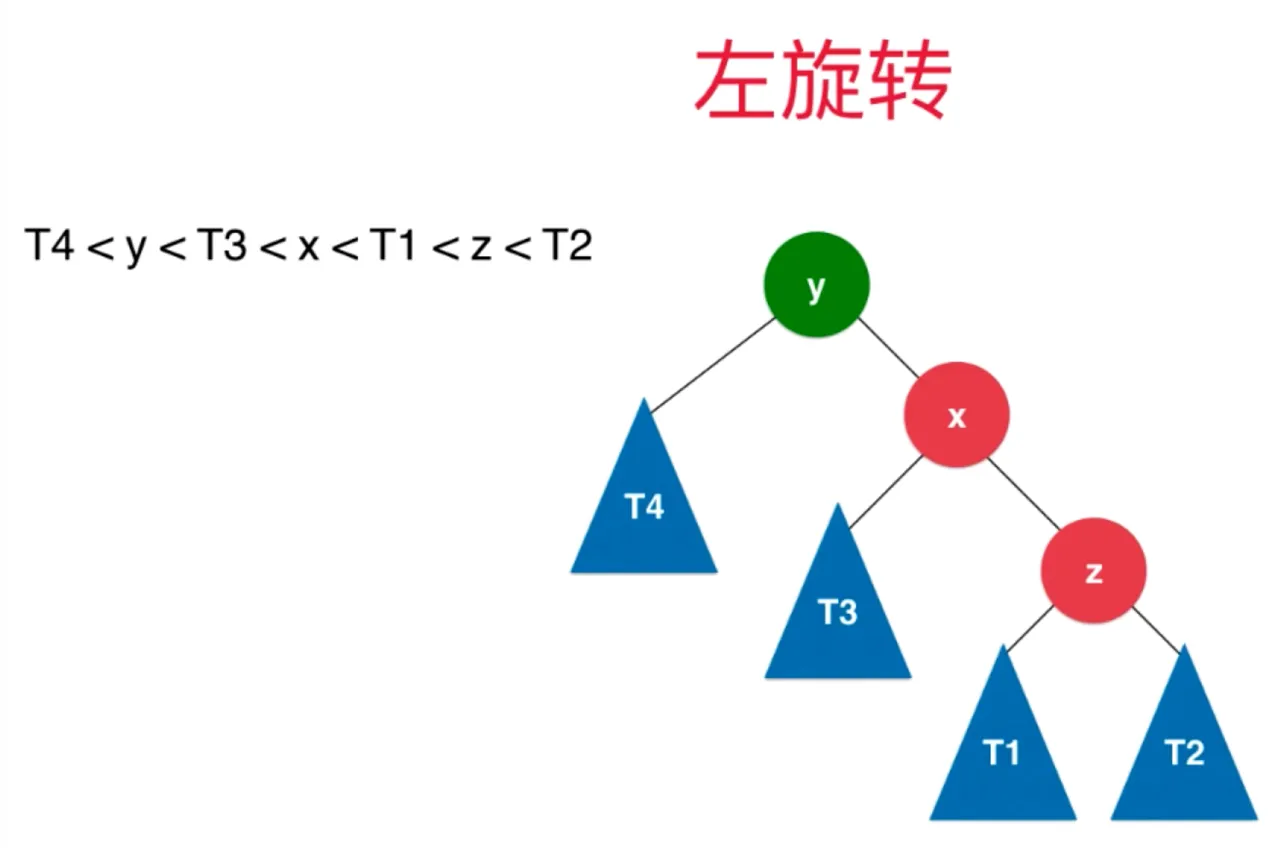 x.left = y
x.left = y
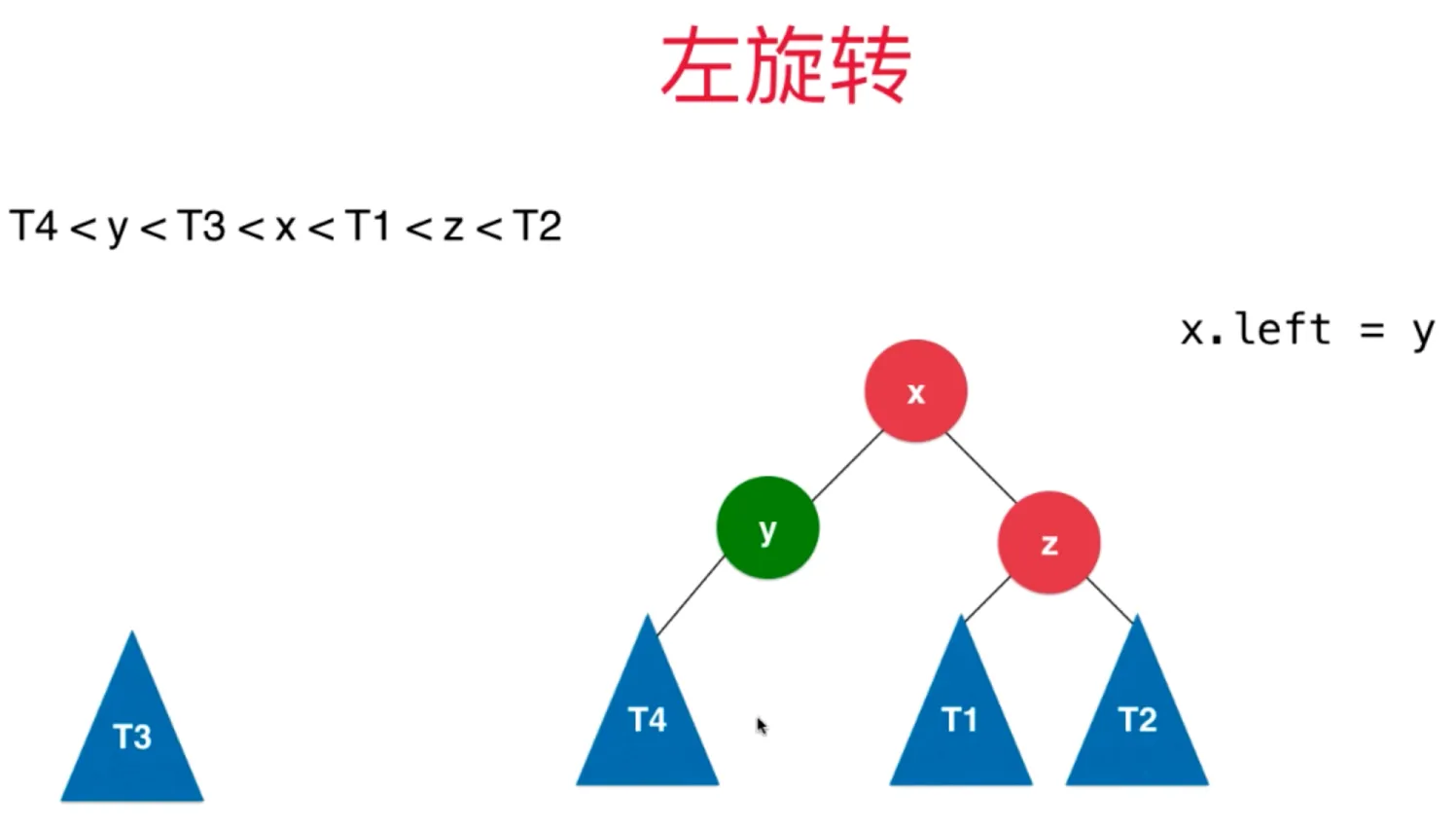 y.right = T3
y.right = T3
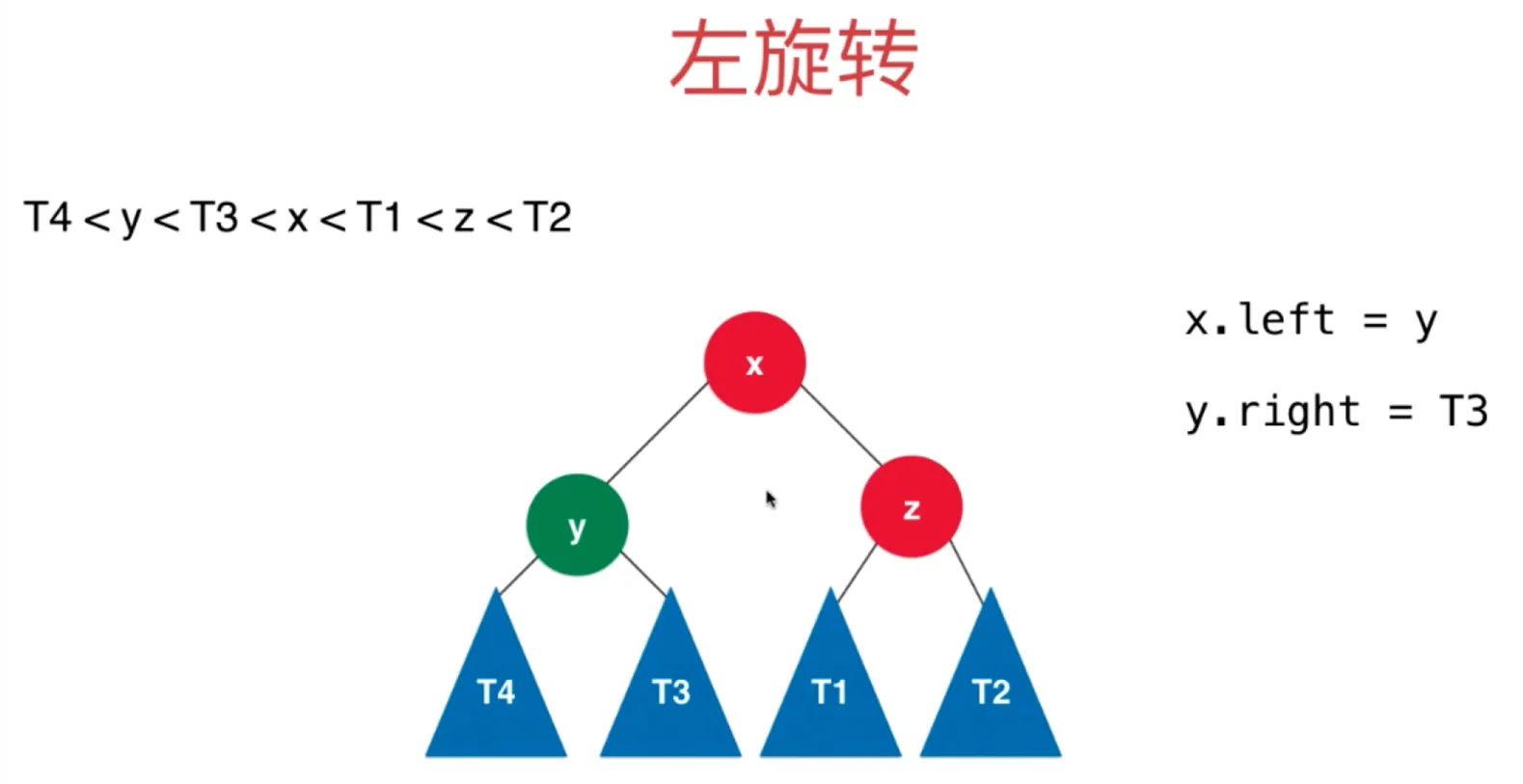
前面讨论的可以叫做 LL, RR
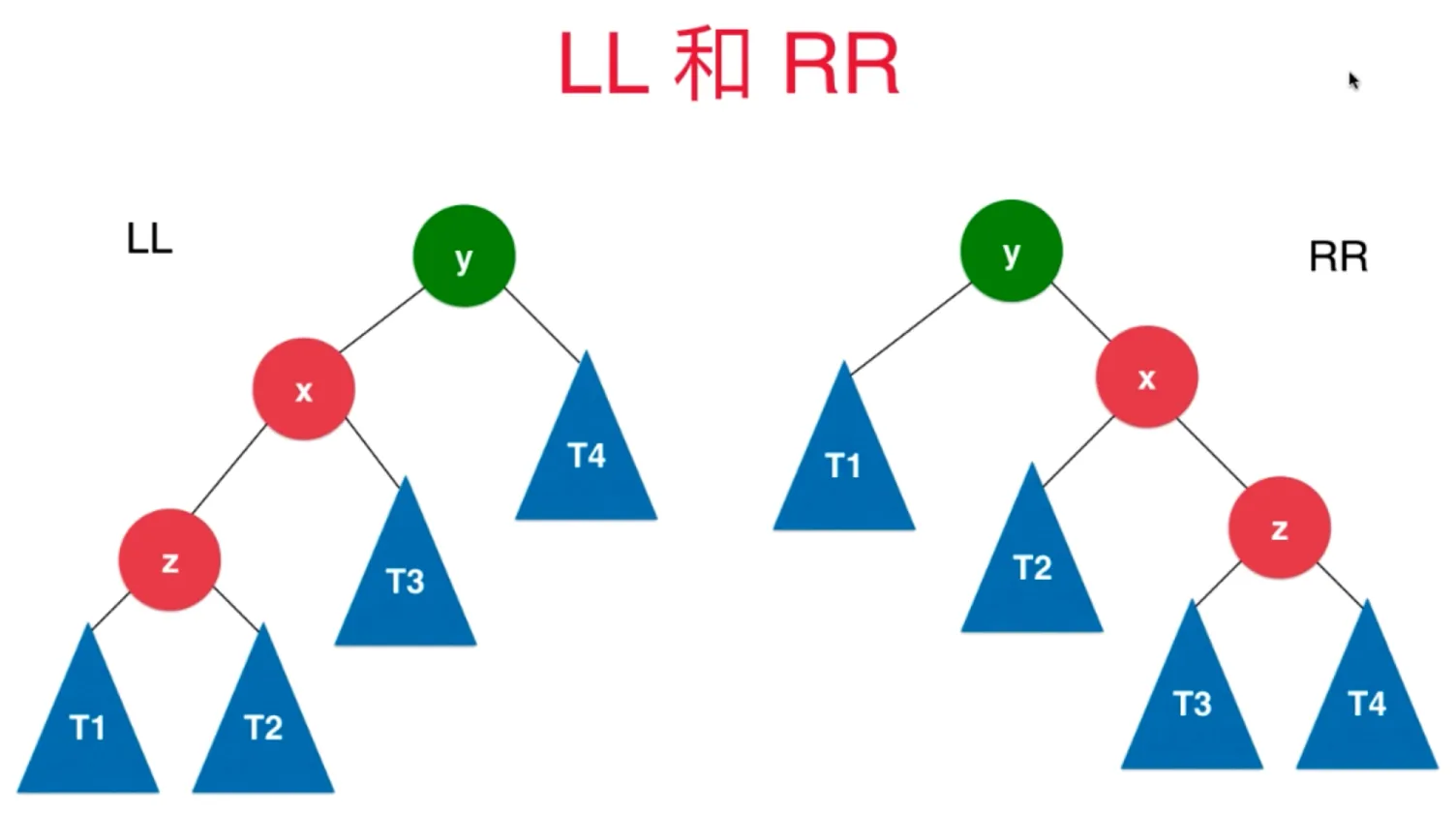
LR
插入的元素在不平衡的节点的左侧的右侧
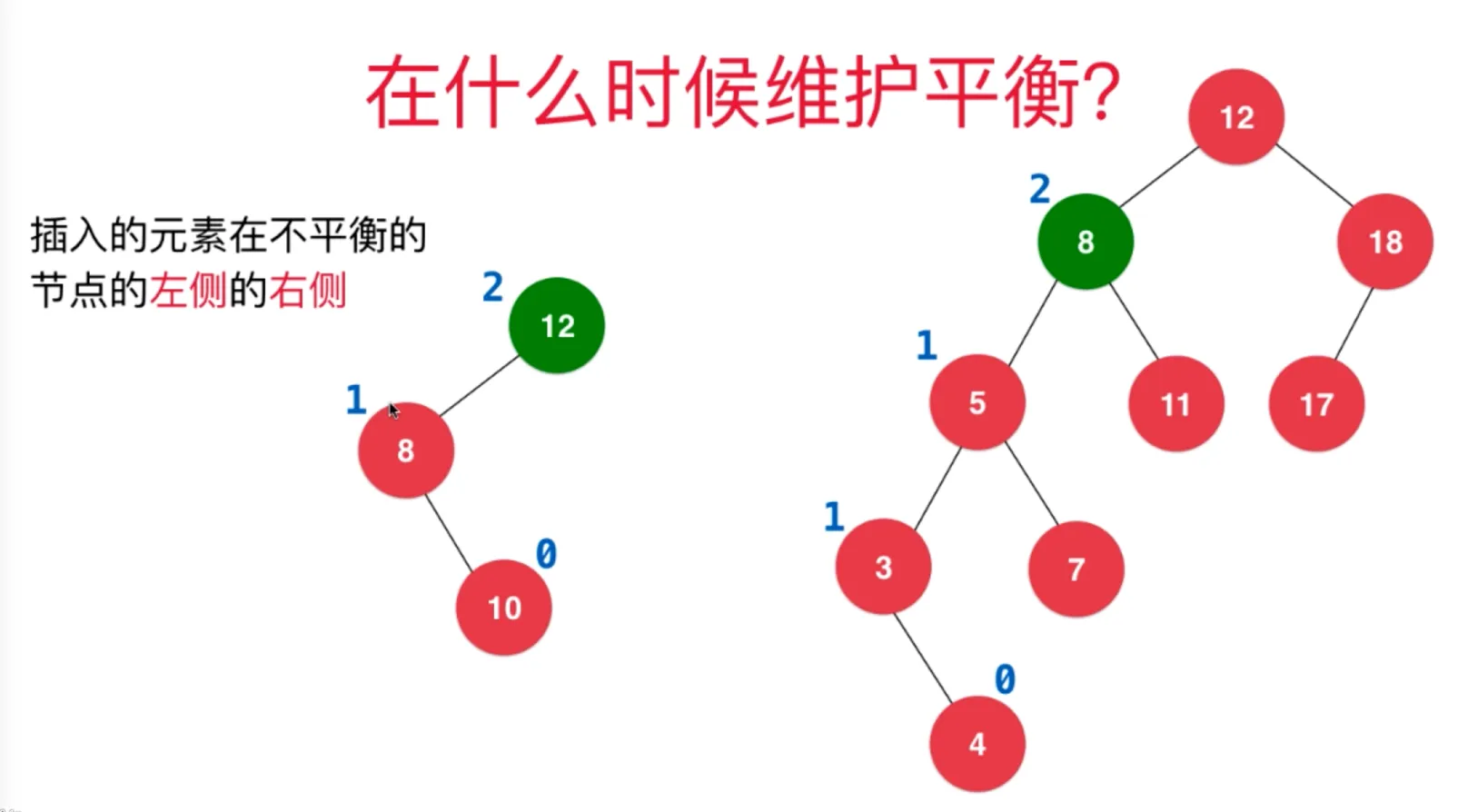 首先对 x 进行左旋转
首先对 x 进行左旋转
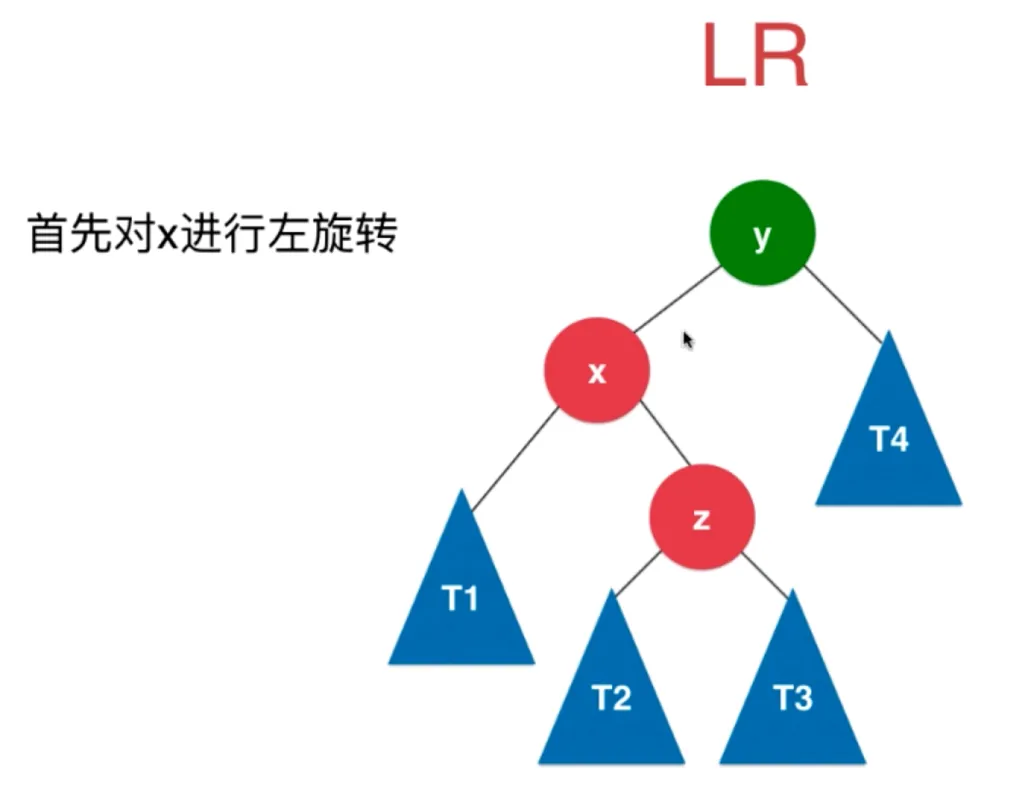 转化成了 LL 的情况
转化成了 LL 的情况
RL
插入的元素在不平衡的节点的右侧的左侧
首先对 x 进行右旋转
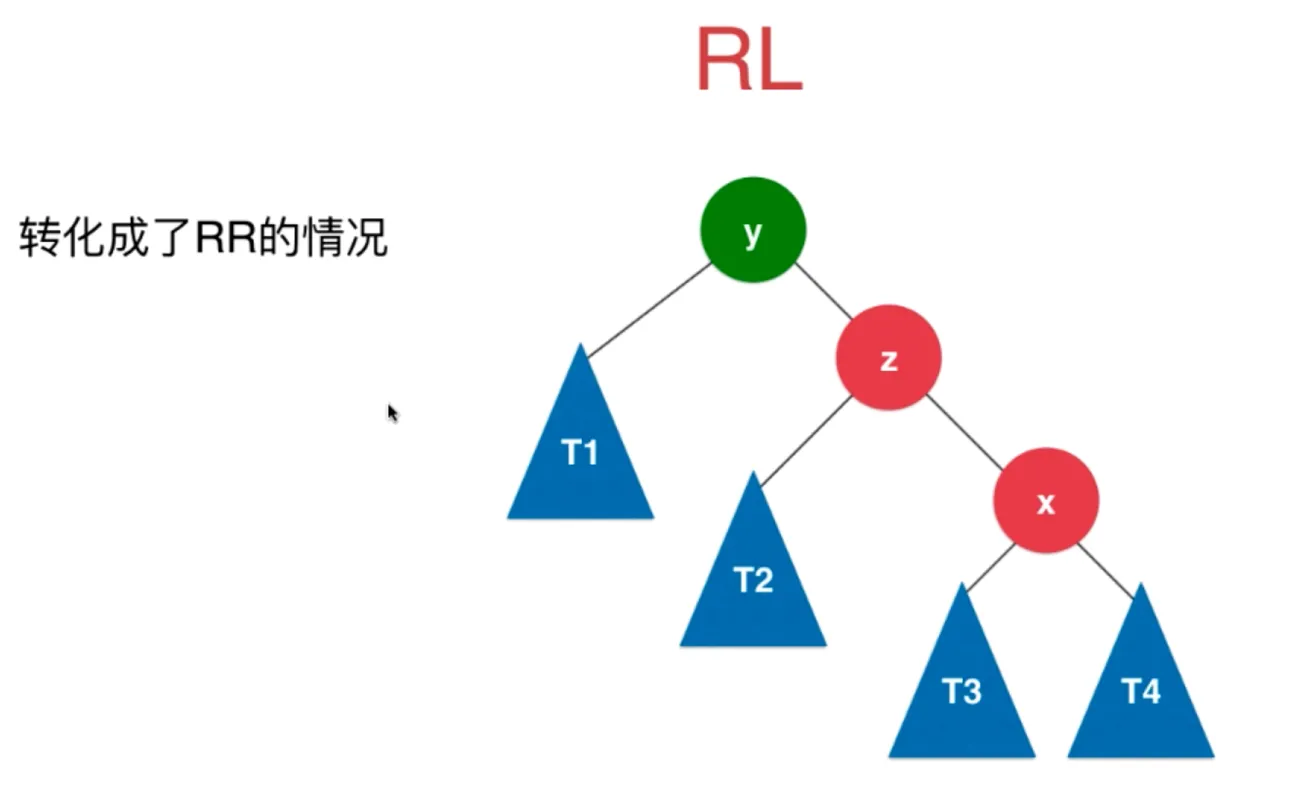
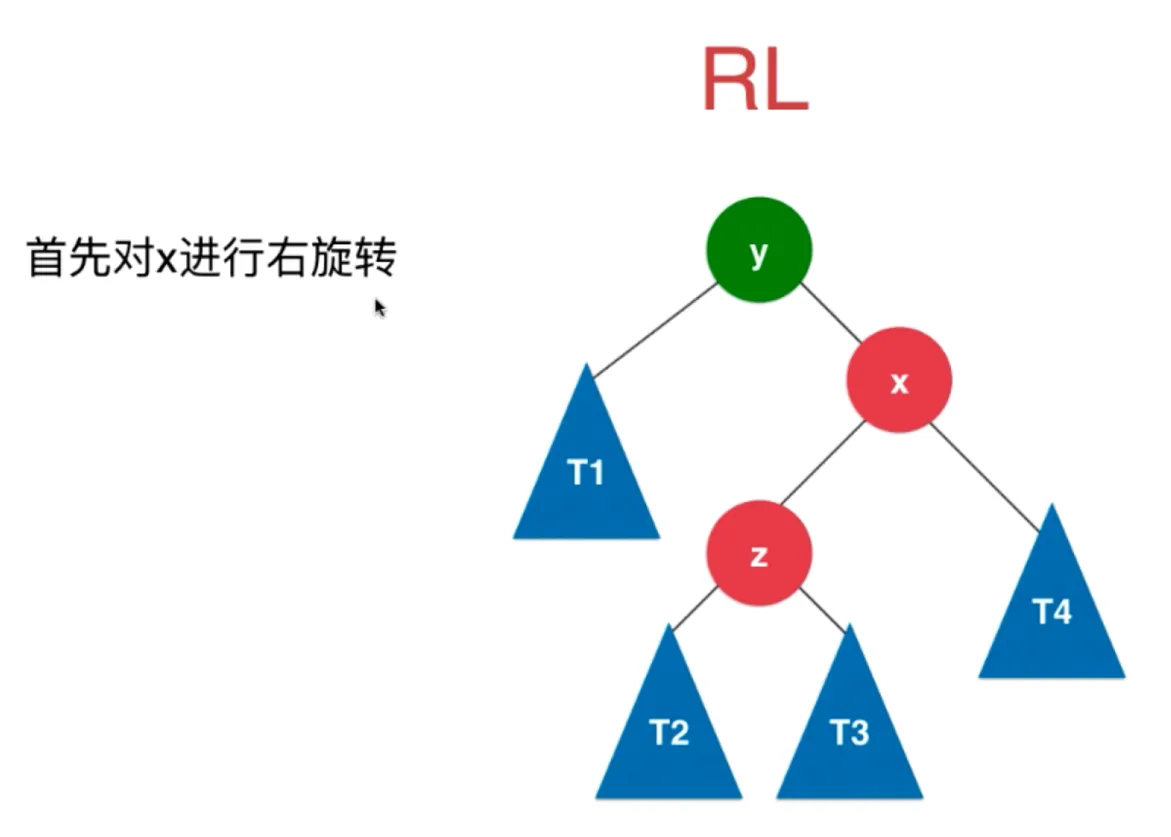 转化成了 RR 的情况
转化成了 RR 的情况
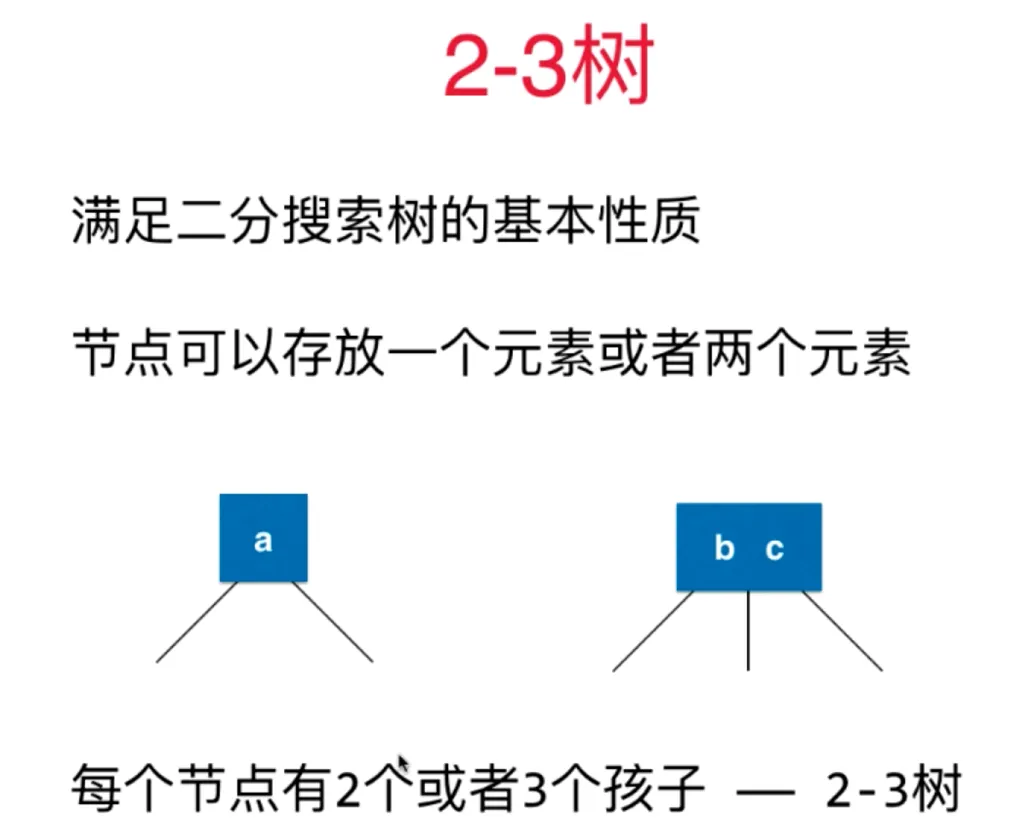
2-3 树
满足二分搜索树的基本性质(对任意节点,大于左节点,小于右节点,对于有两个元素的节点同样,左 < 根1 < 中 < 根2 < 右)
节点可以存放一个元素,或者两个元素
 2-3 树是一颗绝对平衡的树 (从根节点到任意一个叶子节点,所经过的节点数量一定是相同的)
2-3 树是一颗绝对平衡的树 (从根节点到任意一个叶子节点,所经过的节点数量一定是相同的)
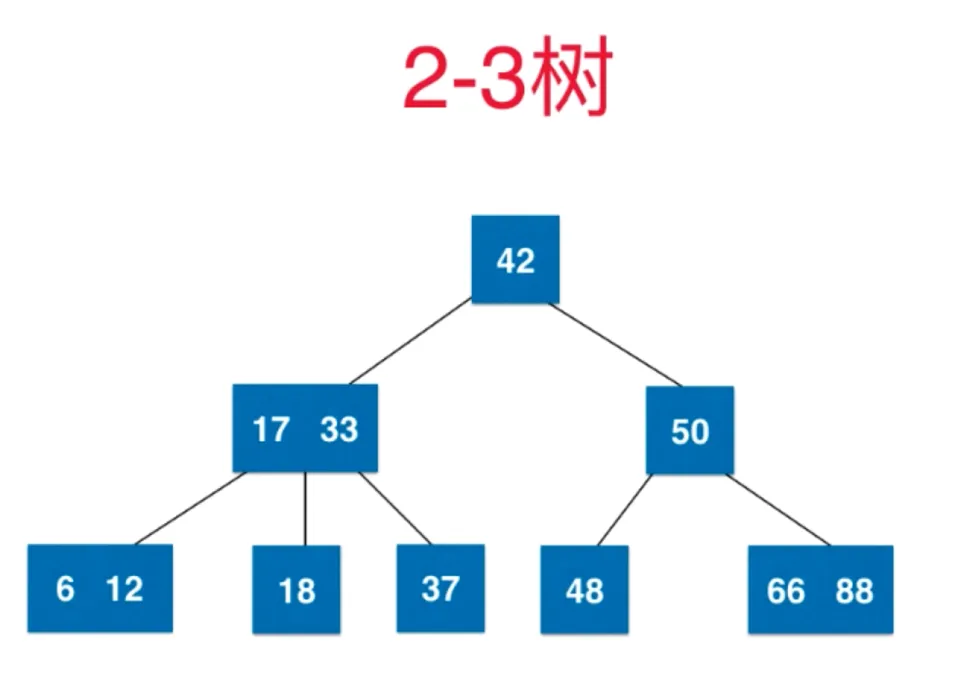
2-3 树如何维护绝对的平衡
向,单节点 42 添加 37,本应添加到左子树,为满足绝对平衡性质,融合为单节点
 再添加节点 12,不能添加到空节点,先融合
再添加节点 12,不能添加到空节点,先融合
 再分裂
再分裂
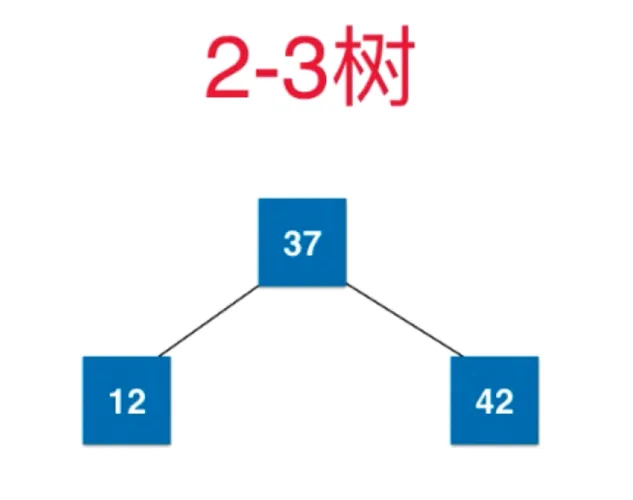 再添加节点 18,本应添加到 12 右子树,12 右子树是空,不会添加,先和 12 融合
再添加节点 18,本应添加到 12 右子树,12 右子树是空,不会添加,先和 12 融合
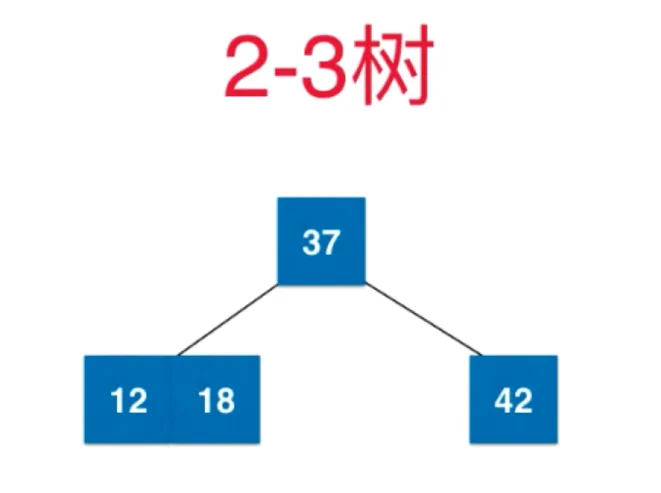 添加 6,先融合
添加 6,先融合
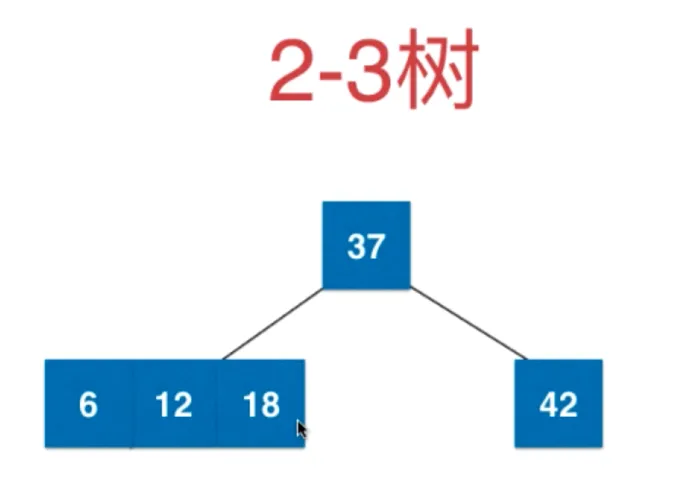 如果这样拆解就不绝对平衡了
如果这样拆解就不绝对平衡了
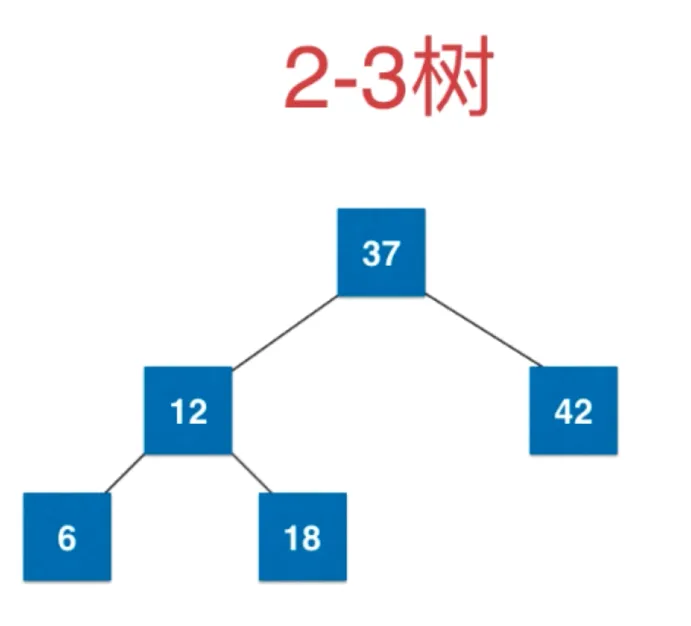 应该把中间节点向父节点融合,如果父亲节点只有一个元素,直接融合即可
应该把中间节点向父节点融合,如果父亲节点只有一个元素,直接融合即可
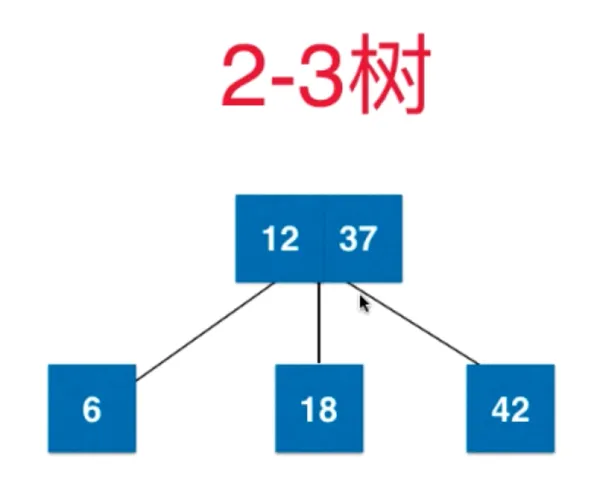 插入 11
插入 11
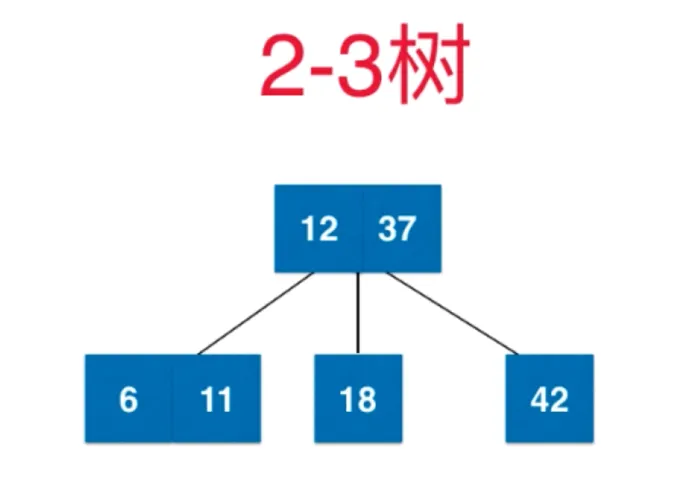 插入 5
插入 5
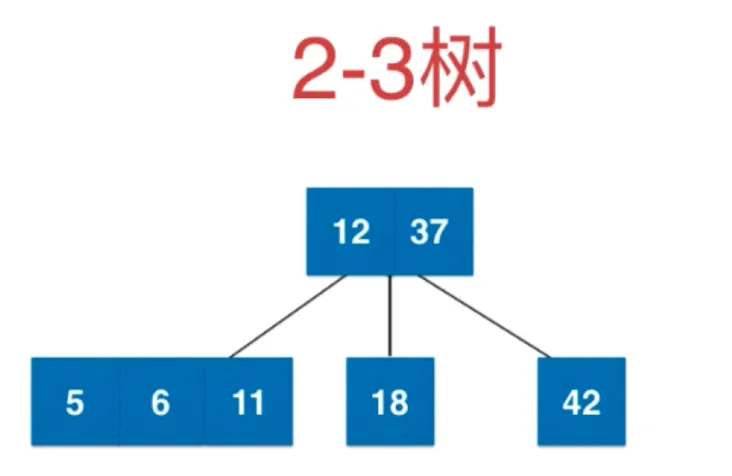 中间节点向父节点融合,但是现在父节点有两个元素了
中间节点向父节点融合,但是现在父节点有两个元素了
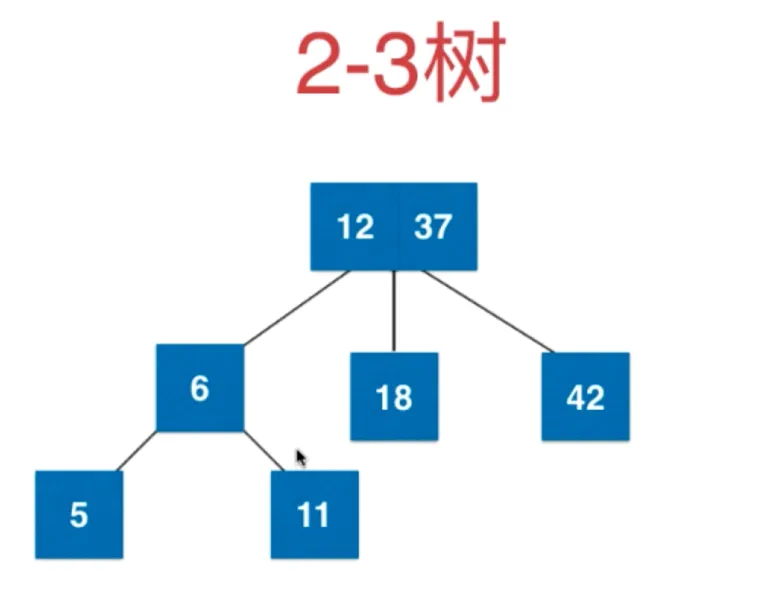 依旧融合
依旧融合
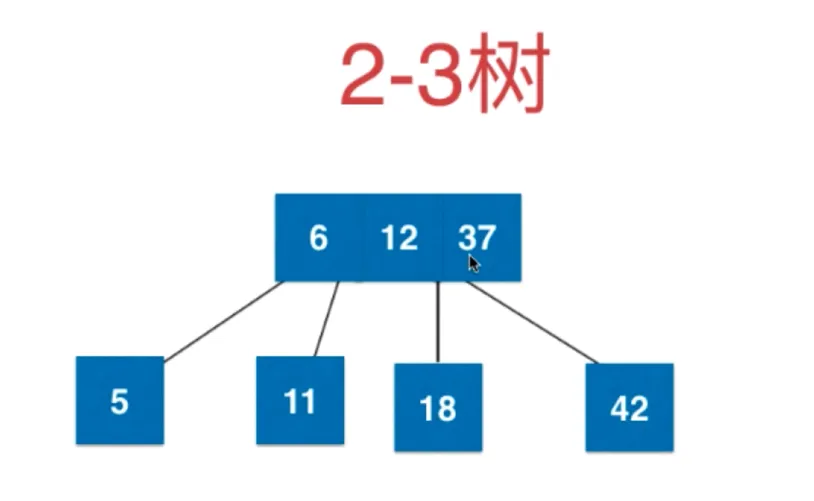 分裂父节点,它没有父节点了,不需要向上融合了
分裂父节点,它没有父节点了,不需要向上融合了
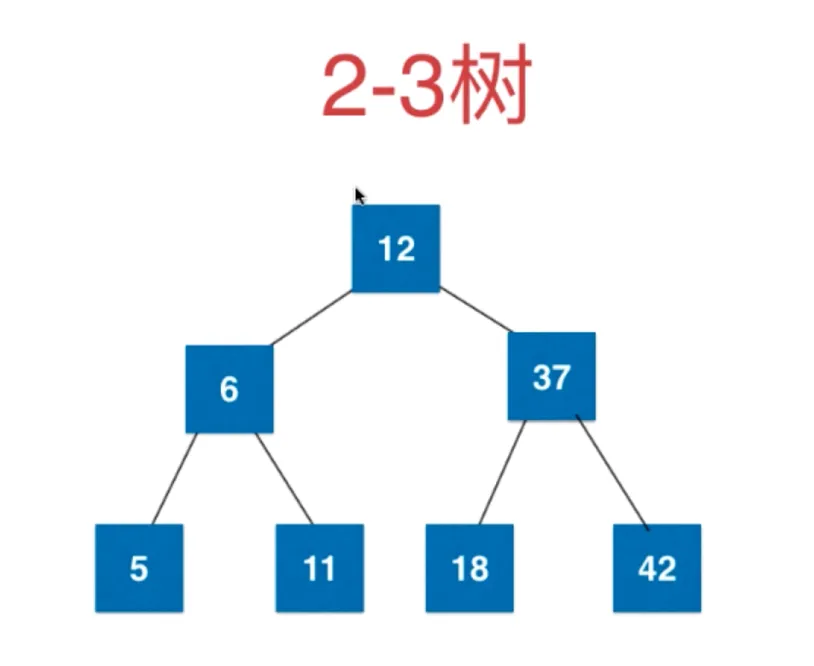
小结
如果插入2-节点
 如果插入3-节点,父节点为2-节点
如果插入3-节点,父节点为2-节点
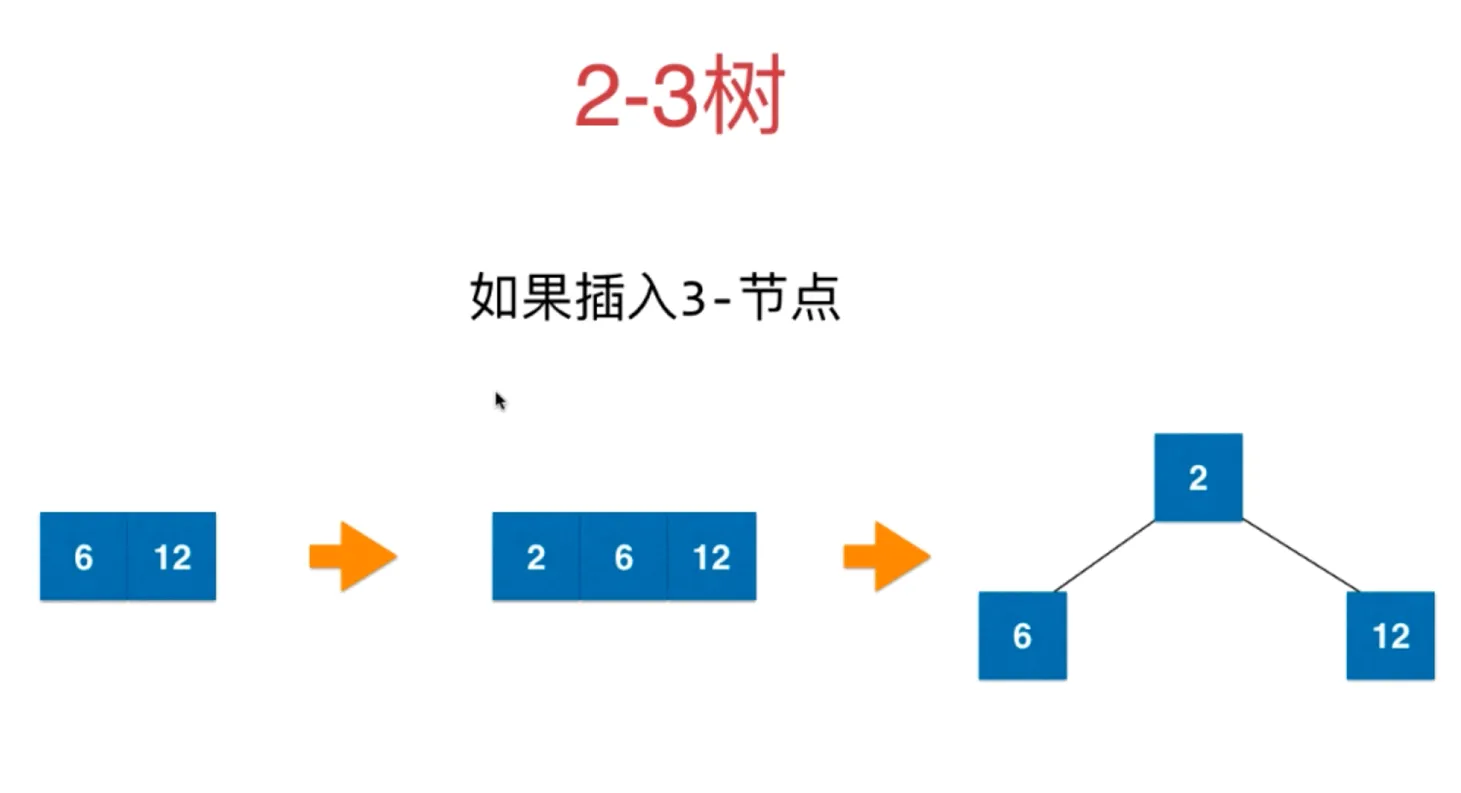
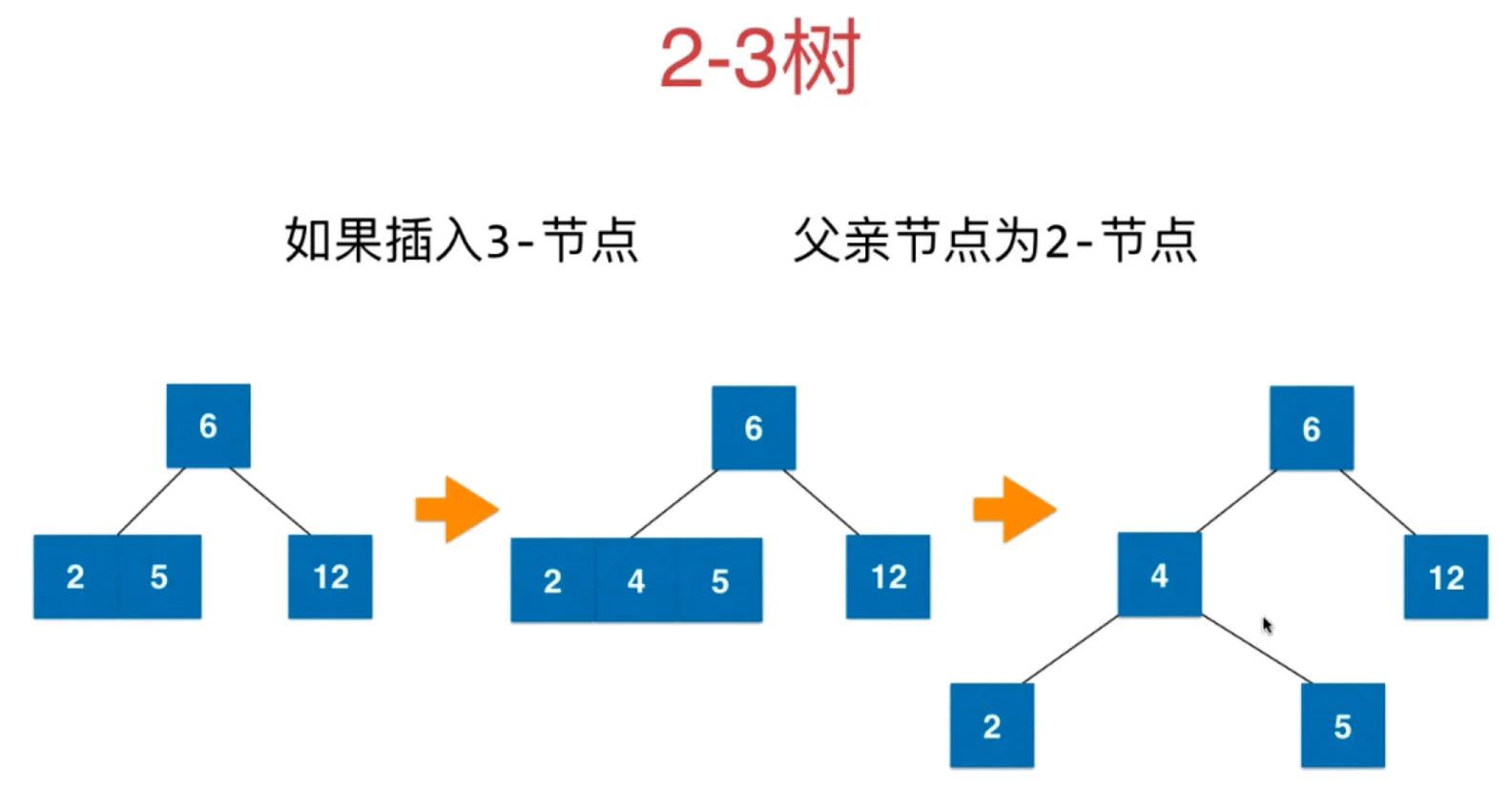
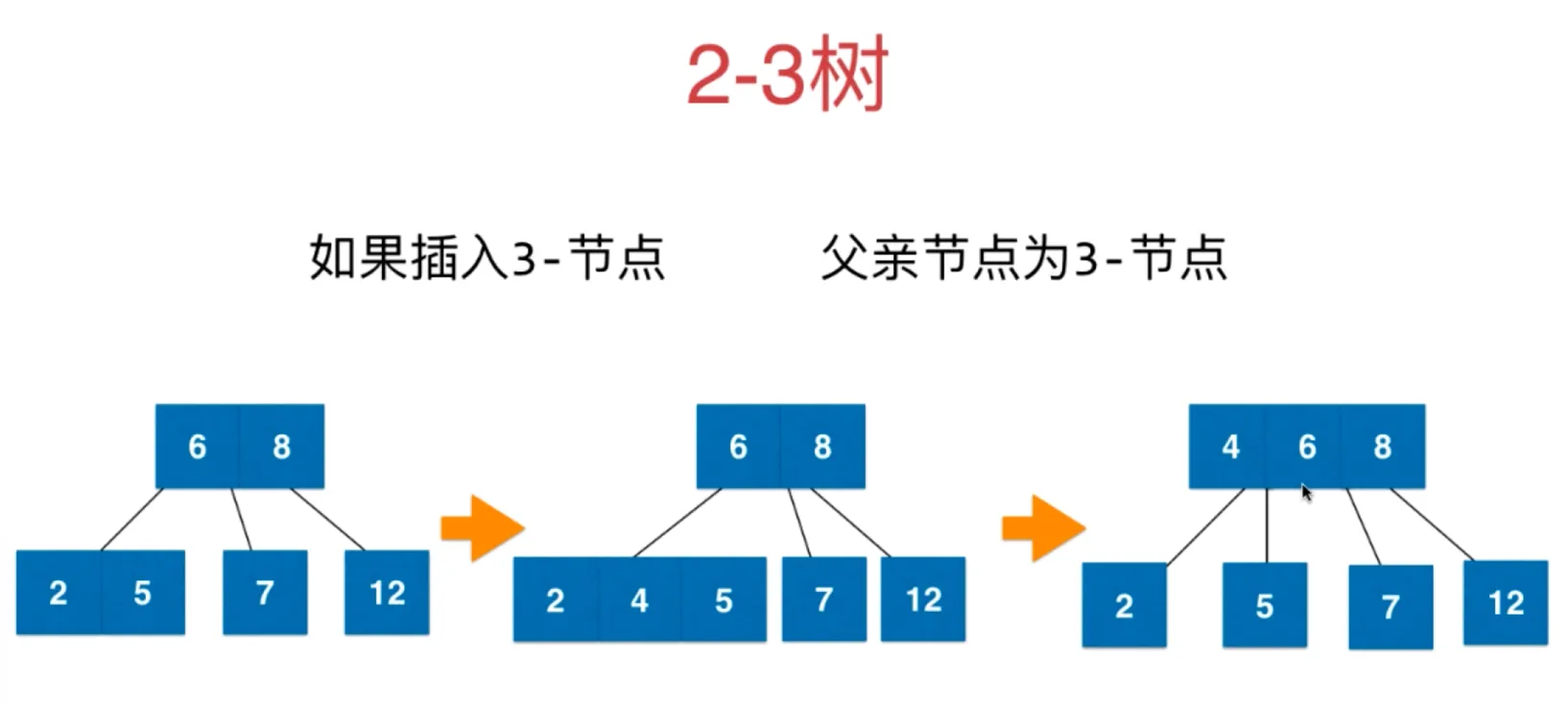
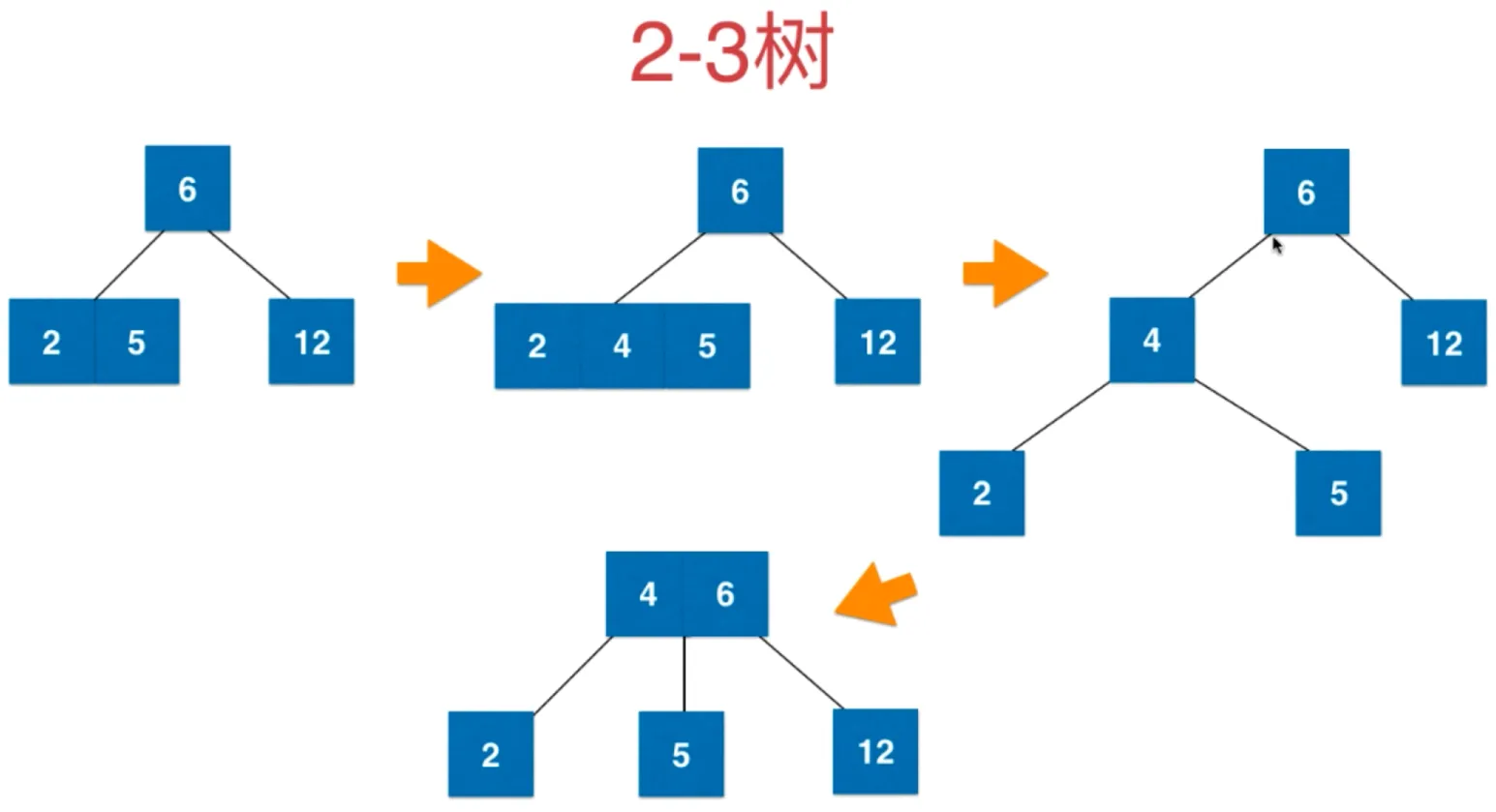 如果插入3-节点,父节点为3-节点
如果插入3-节点,父节点为3-节点
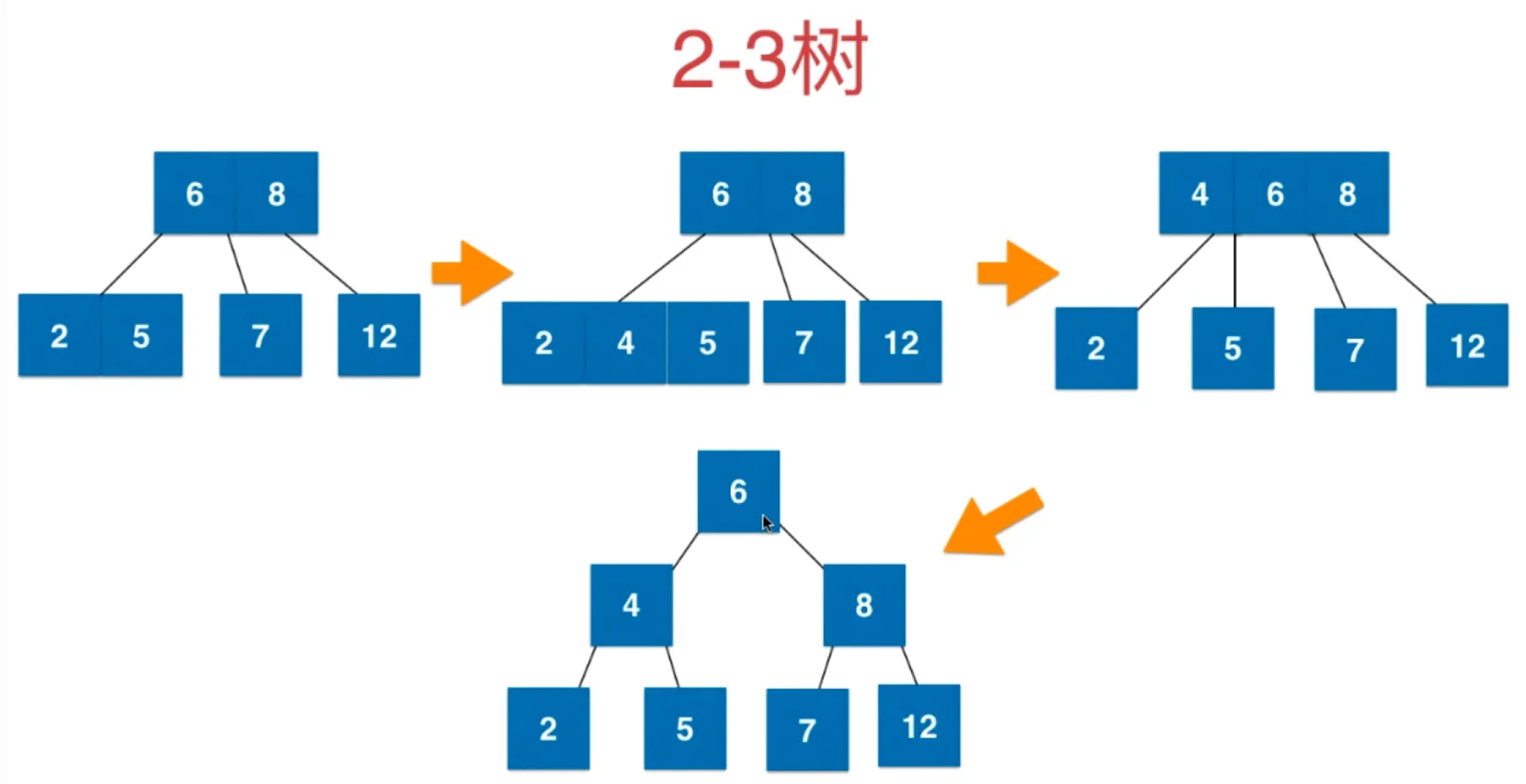
红黑树
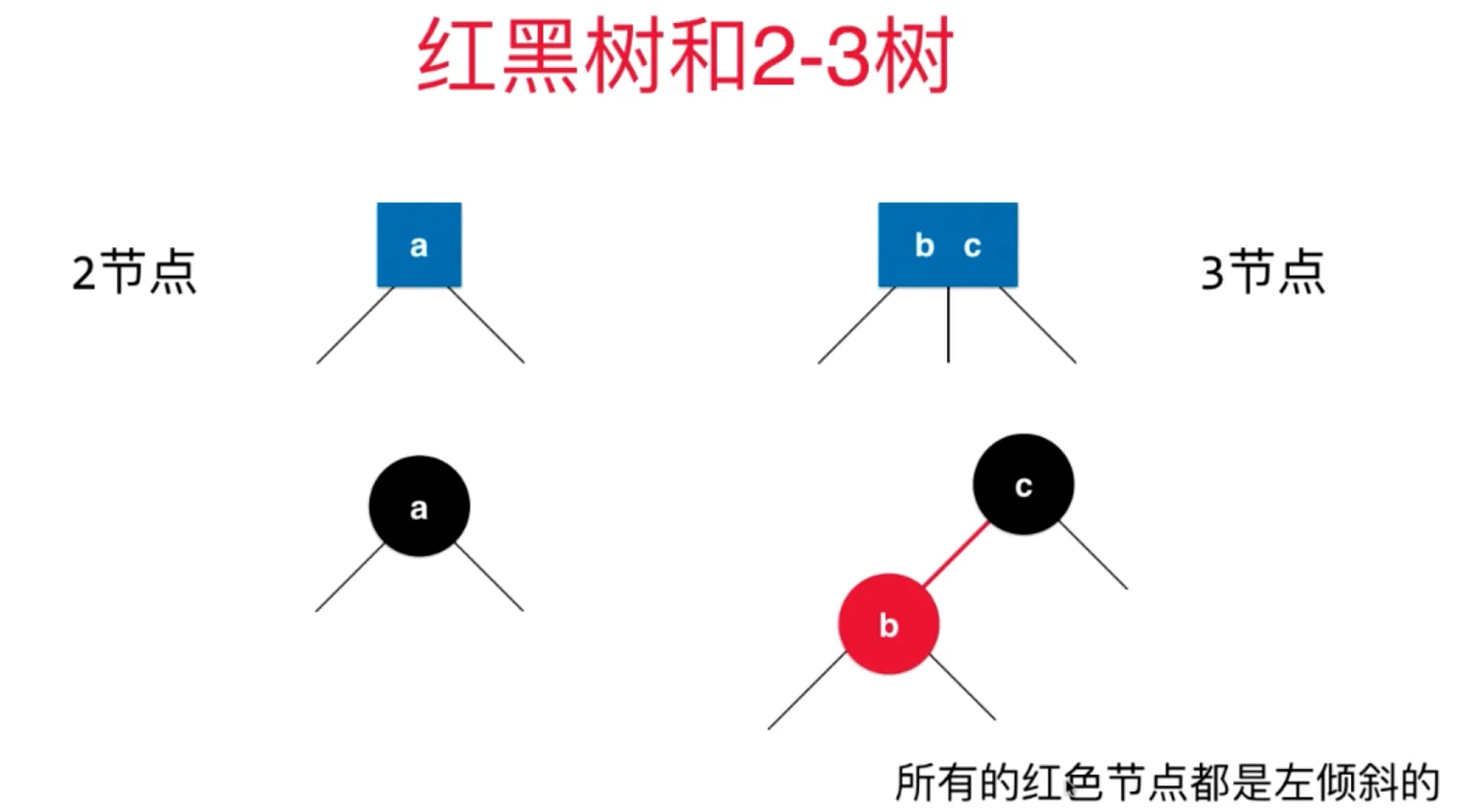
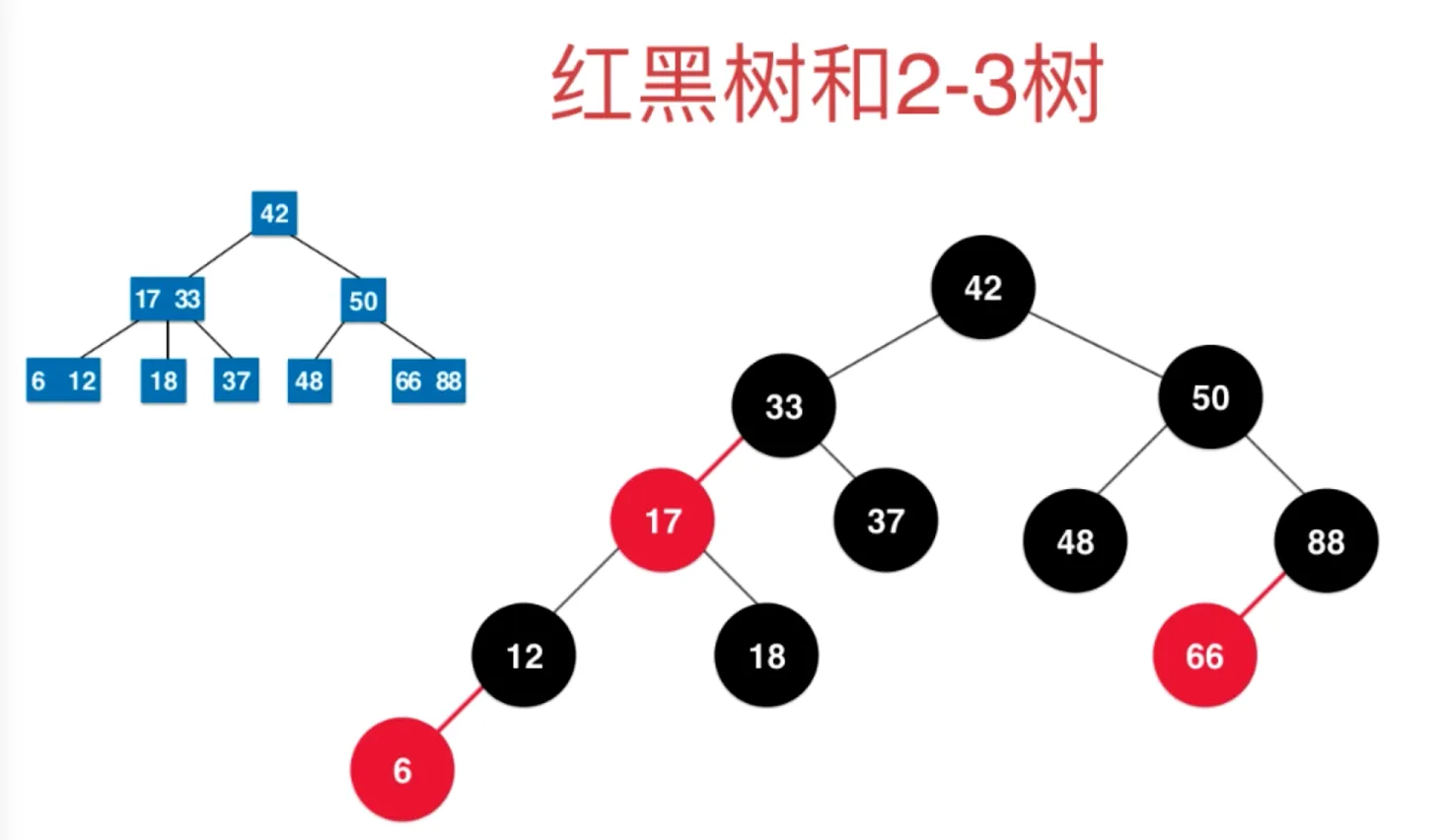
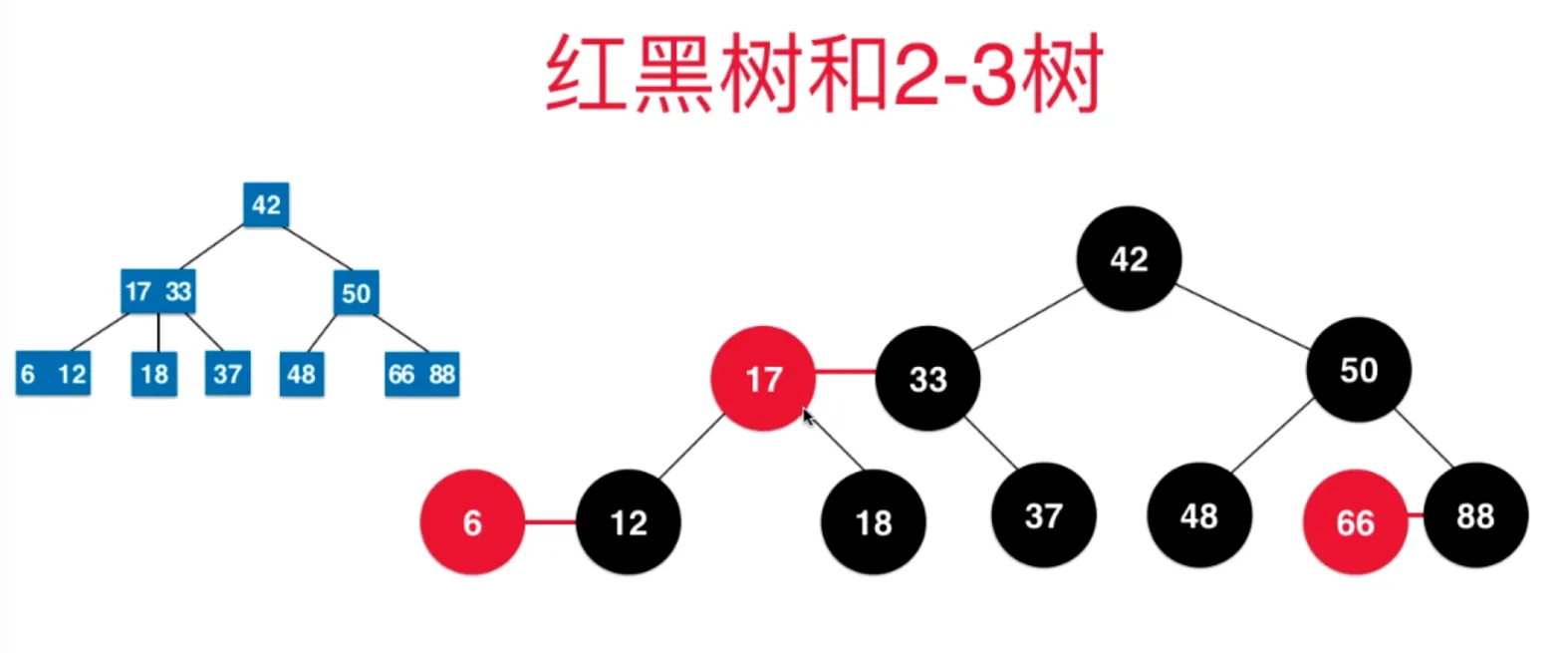
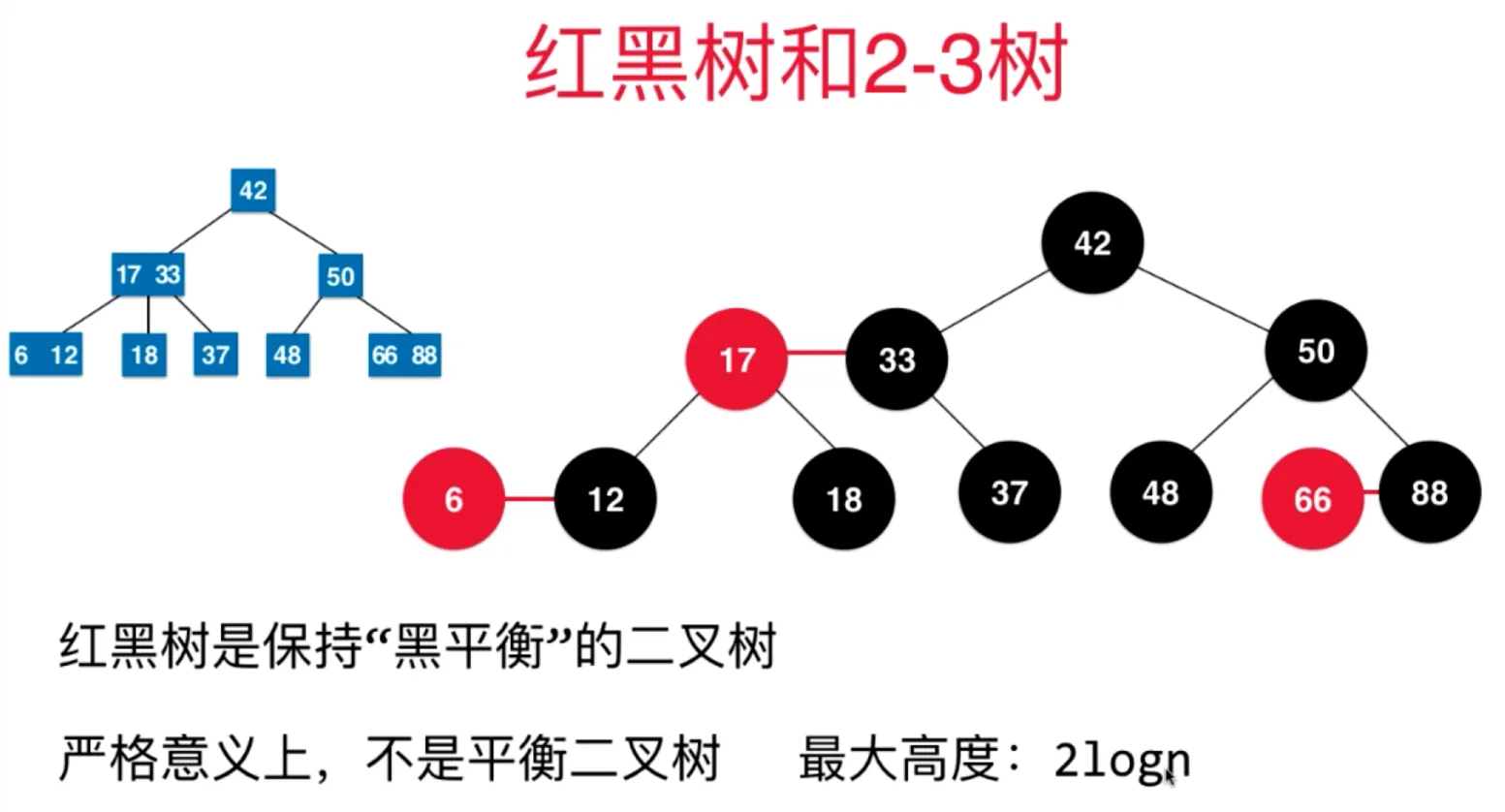
红黑树和2-3树的等价性
2-3树拆分成二分搜索树,可以这样等价
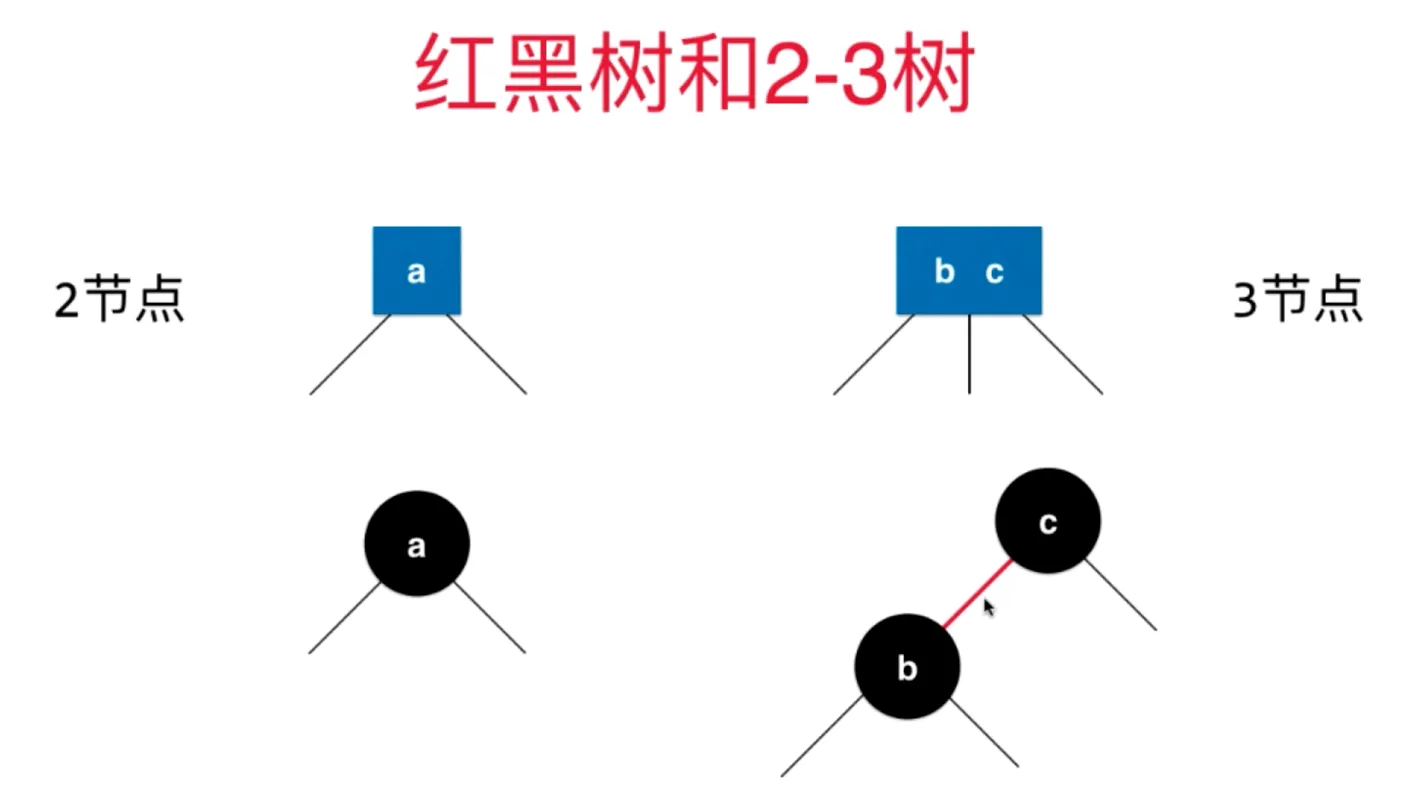 使用红色节点来表示 b和c之间这个特殊的关系
使用红色节点来表示 b和c之间这个特殊的关系

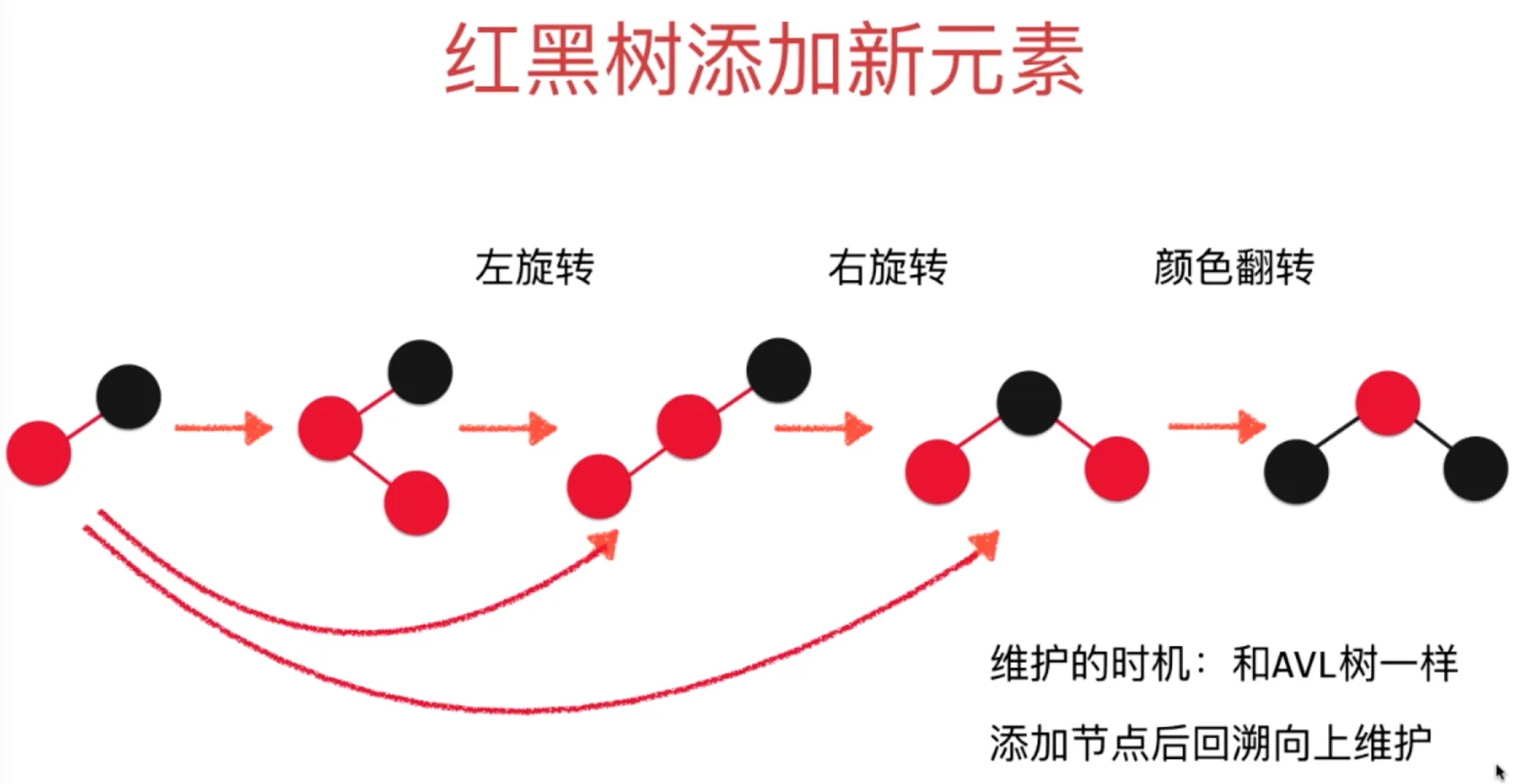
红黑树添加元素
首次添加是红色的(2-3树临时融合进子节点)
 根节点置黑
根节点置黑
 添加到黑节点左侧,直接插入即可
添加到黑节点左侧,直接插入即可
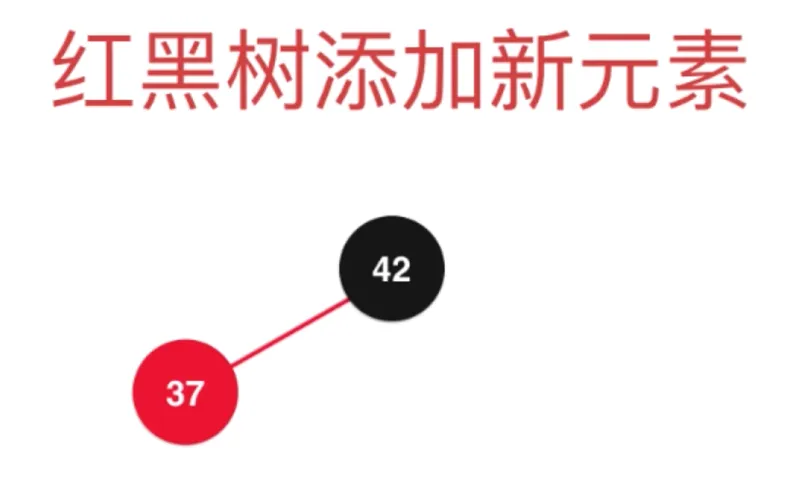 假设应该添加到右子树
假设应该添加到右子树
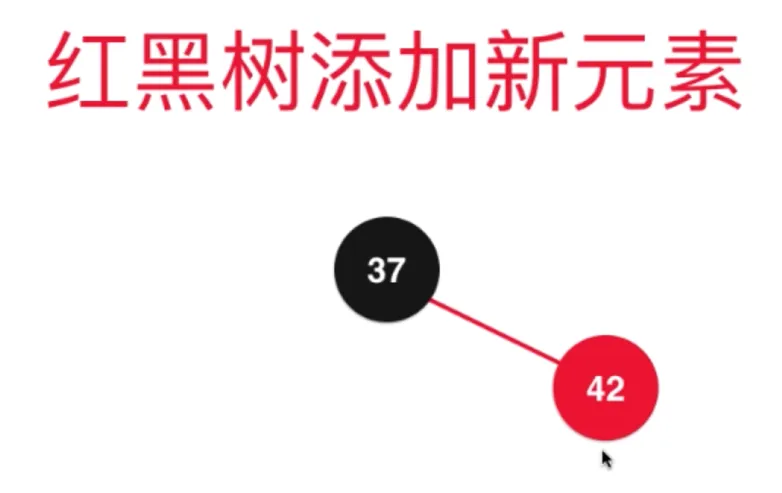 此时需要进行左旋转
此时需要进行左旋转
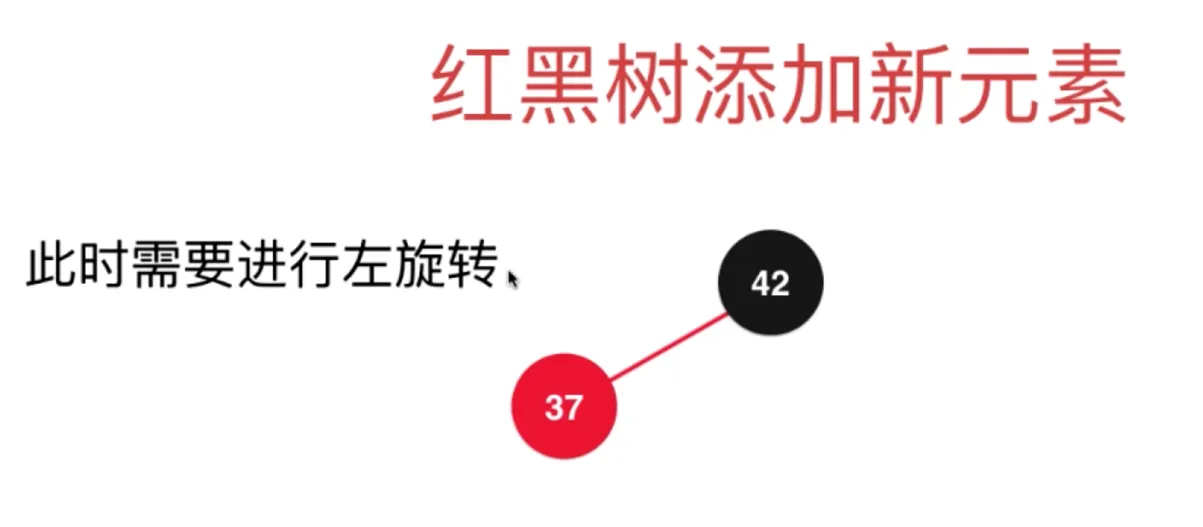 左旋转过程
左旋转过程
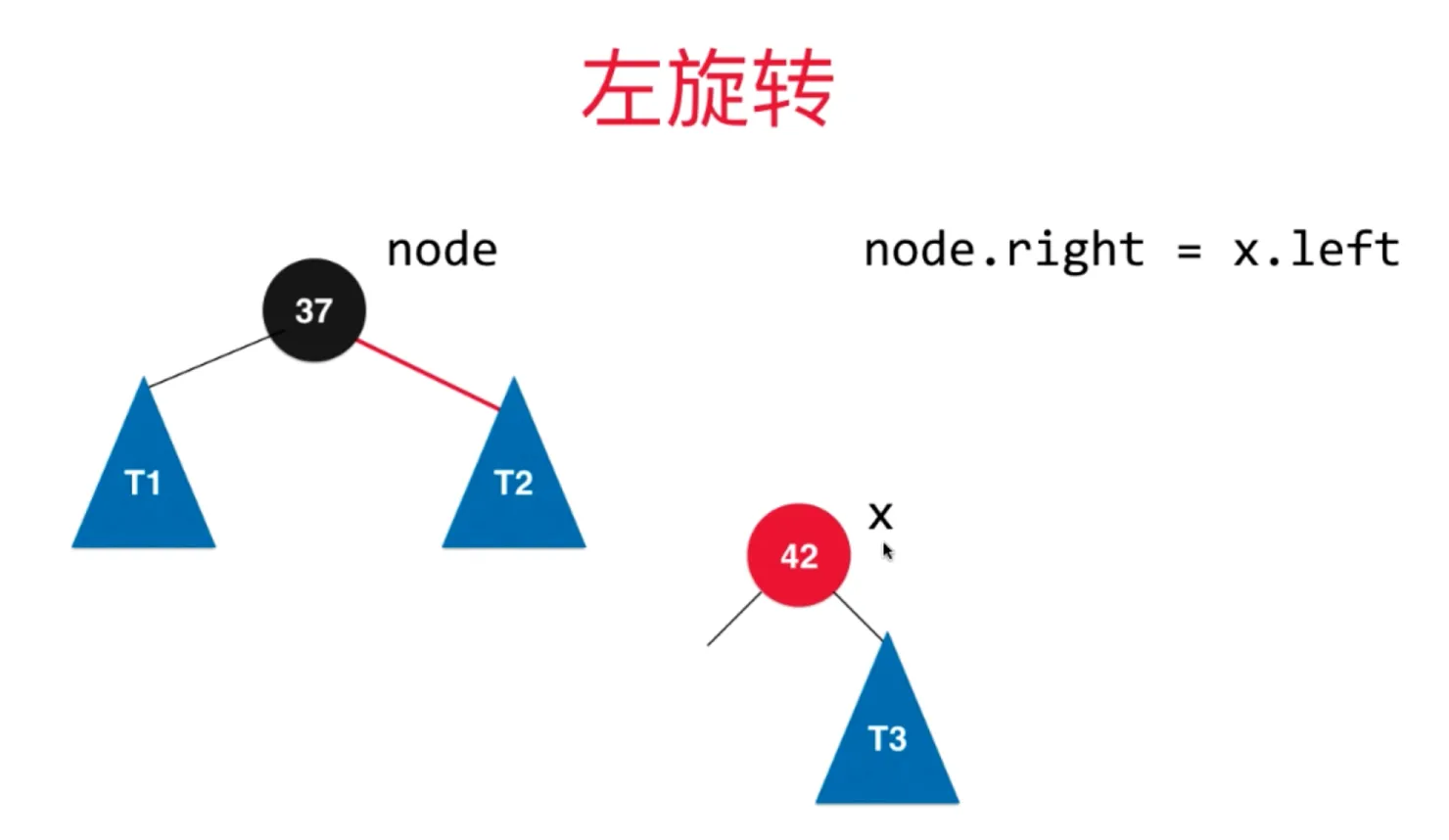
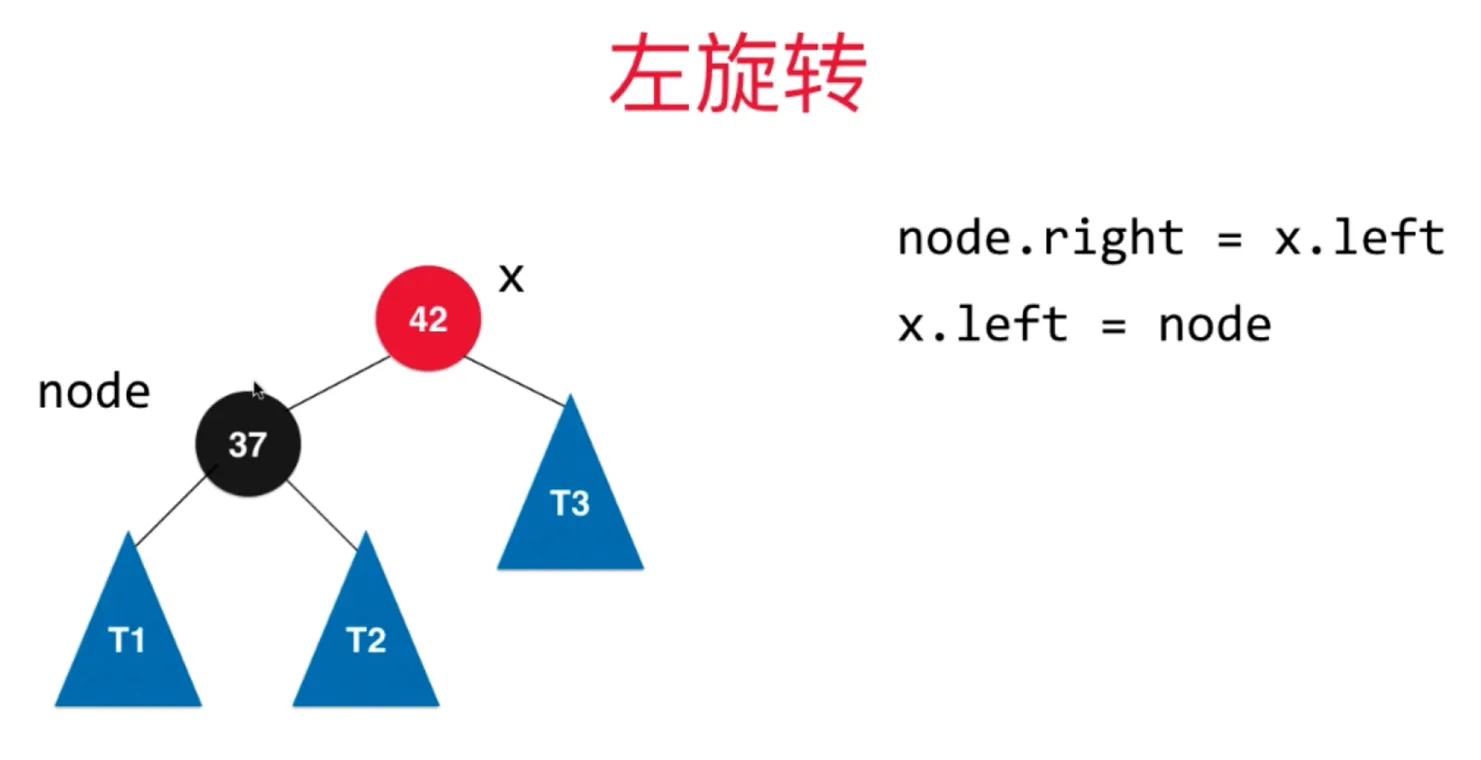
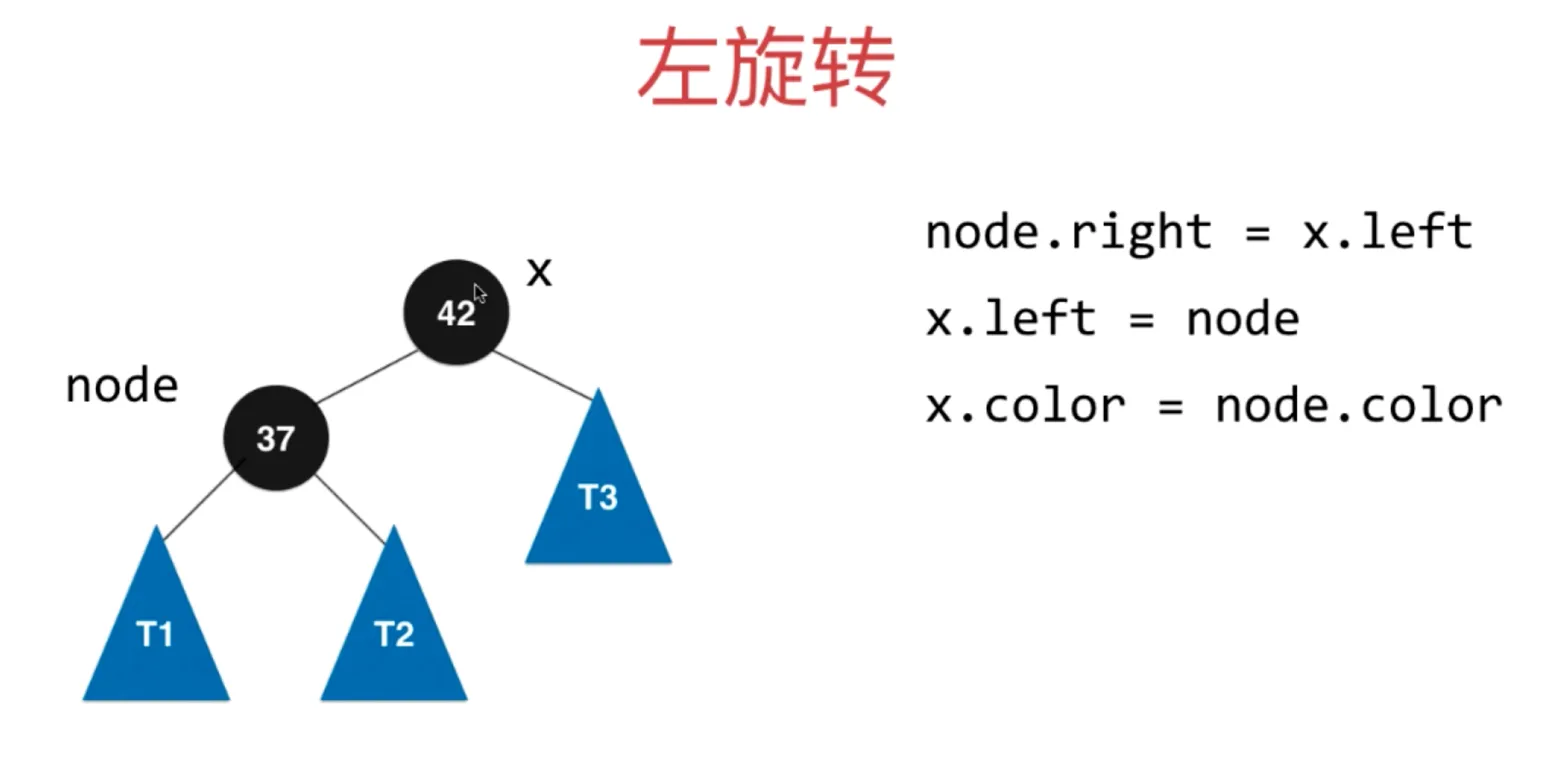
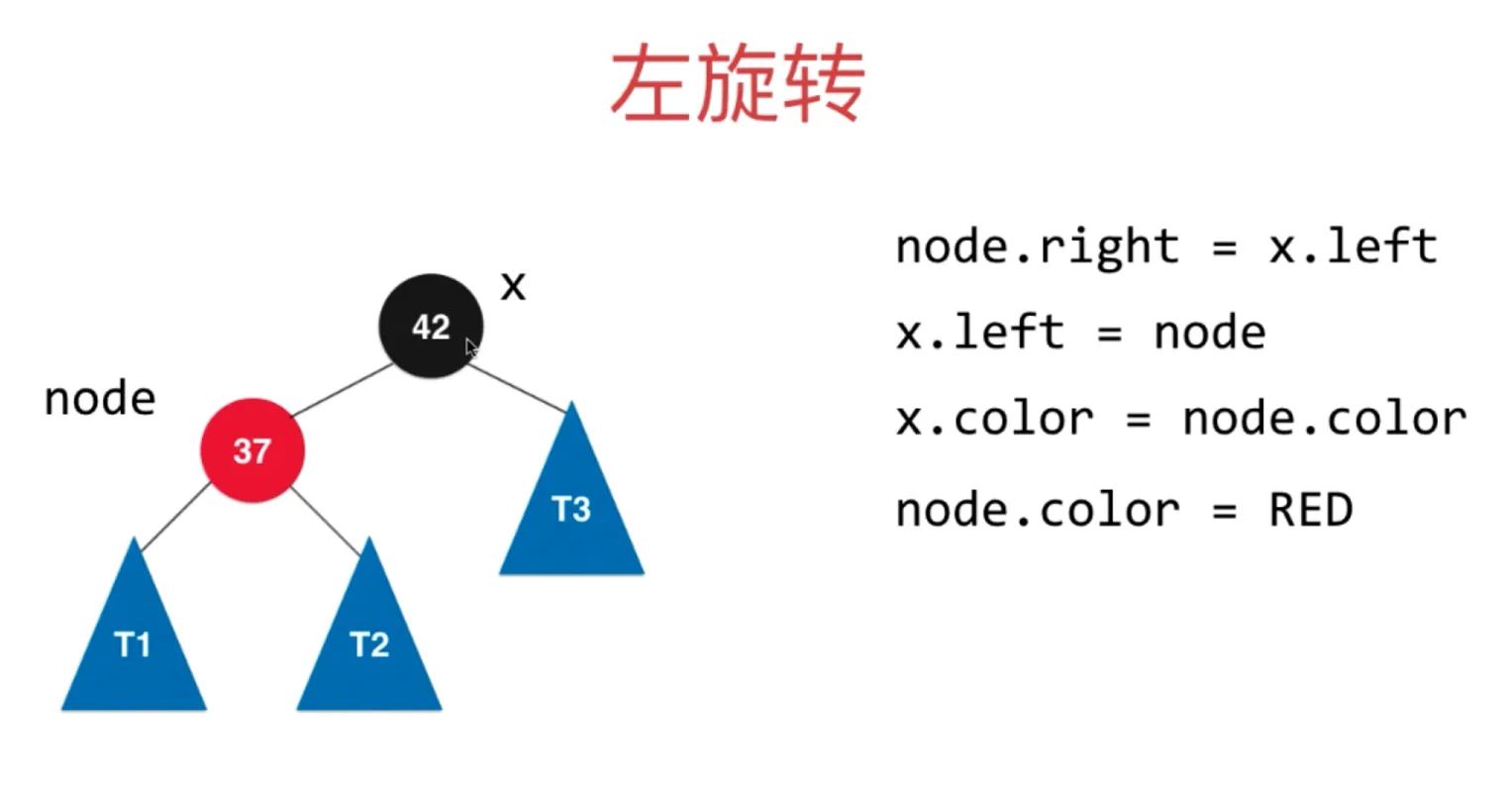
添加节点 66,此时放在右边,此时相当于2-3树的临时4节点
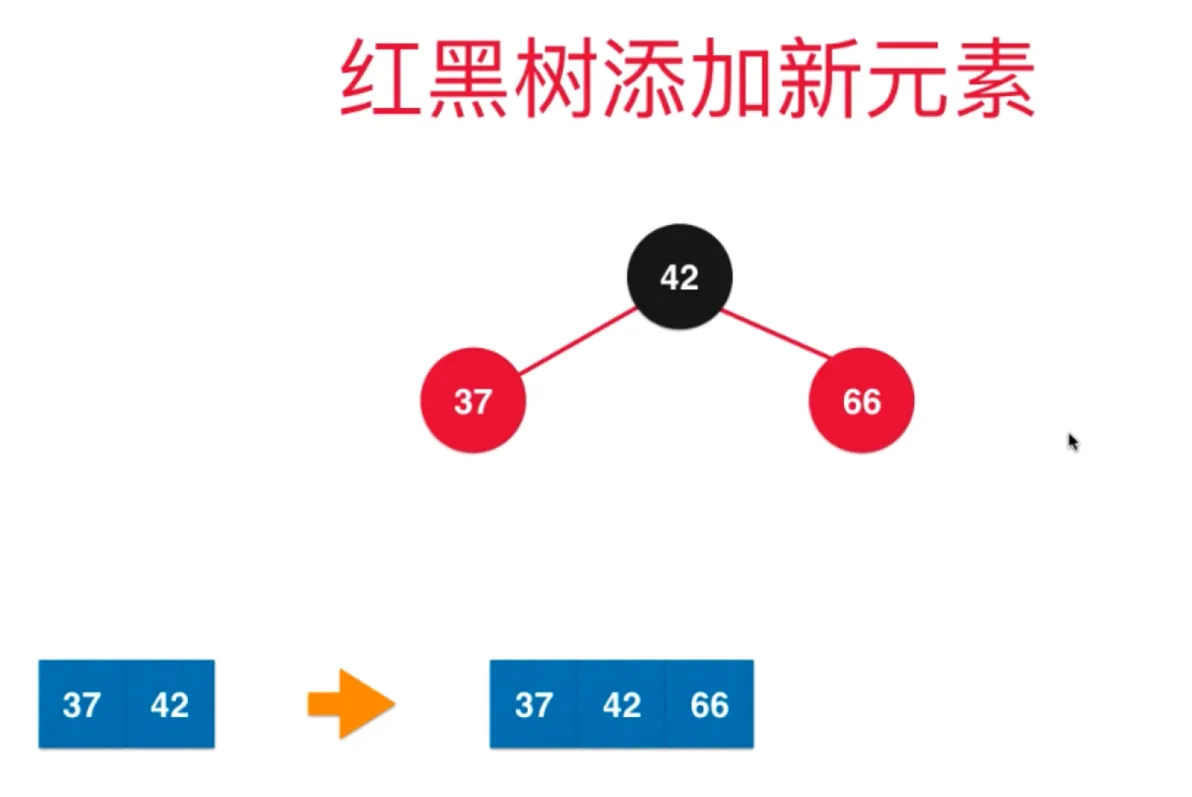 需要把它拆分为三个新节点,对应到红黑树,就是三个节点置黑
需要把它拆分为三个新节点,对应到红黑树,就是三个节点置黑
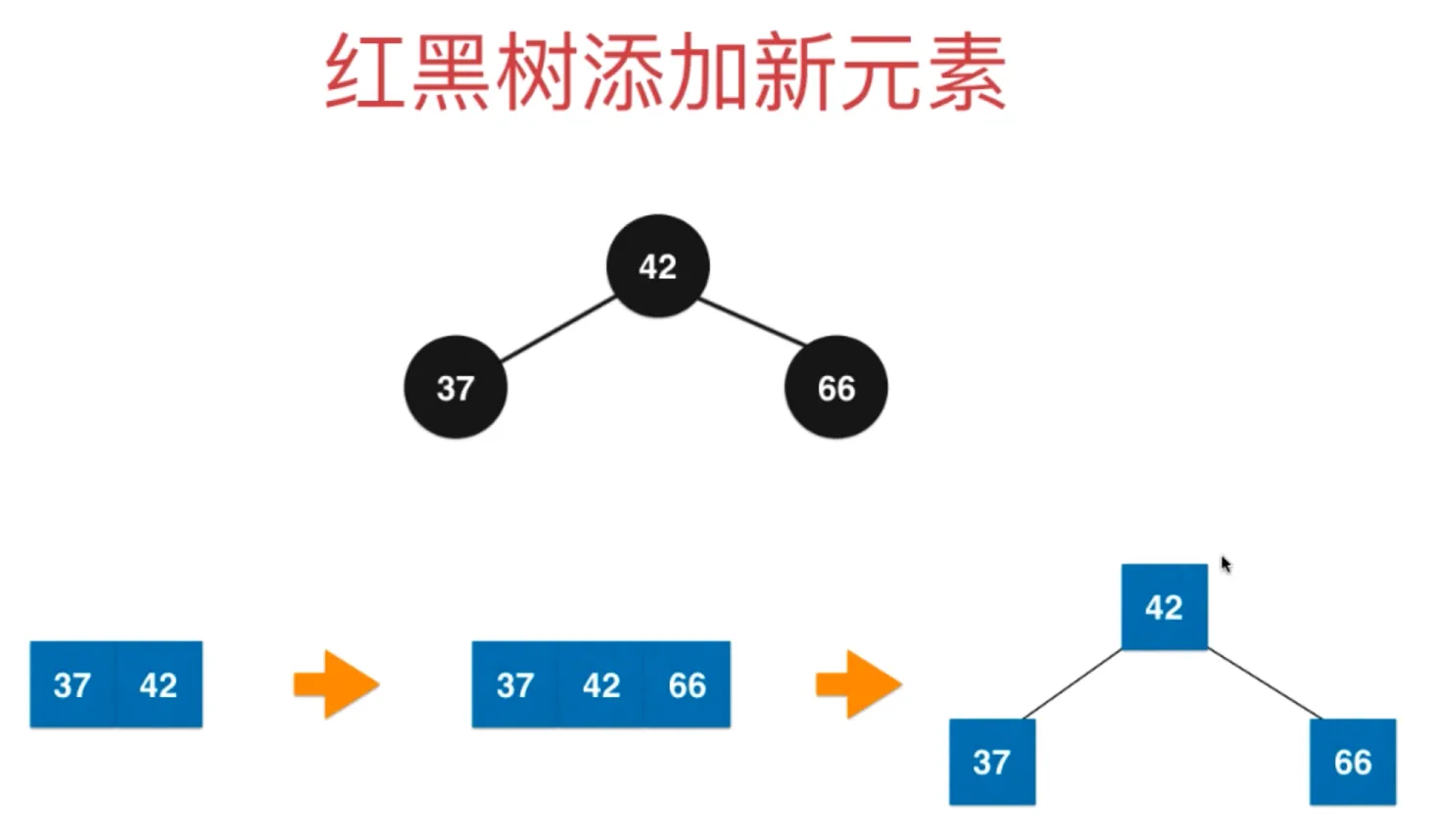 向上融合,根节点置红,这个过程也叫颜色翻转
向上融合,根节点置红,这个过程也叫颜色翻转
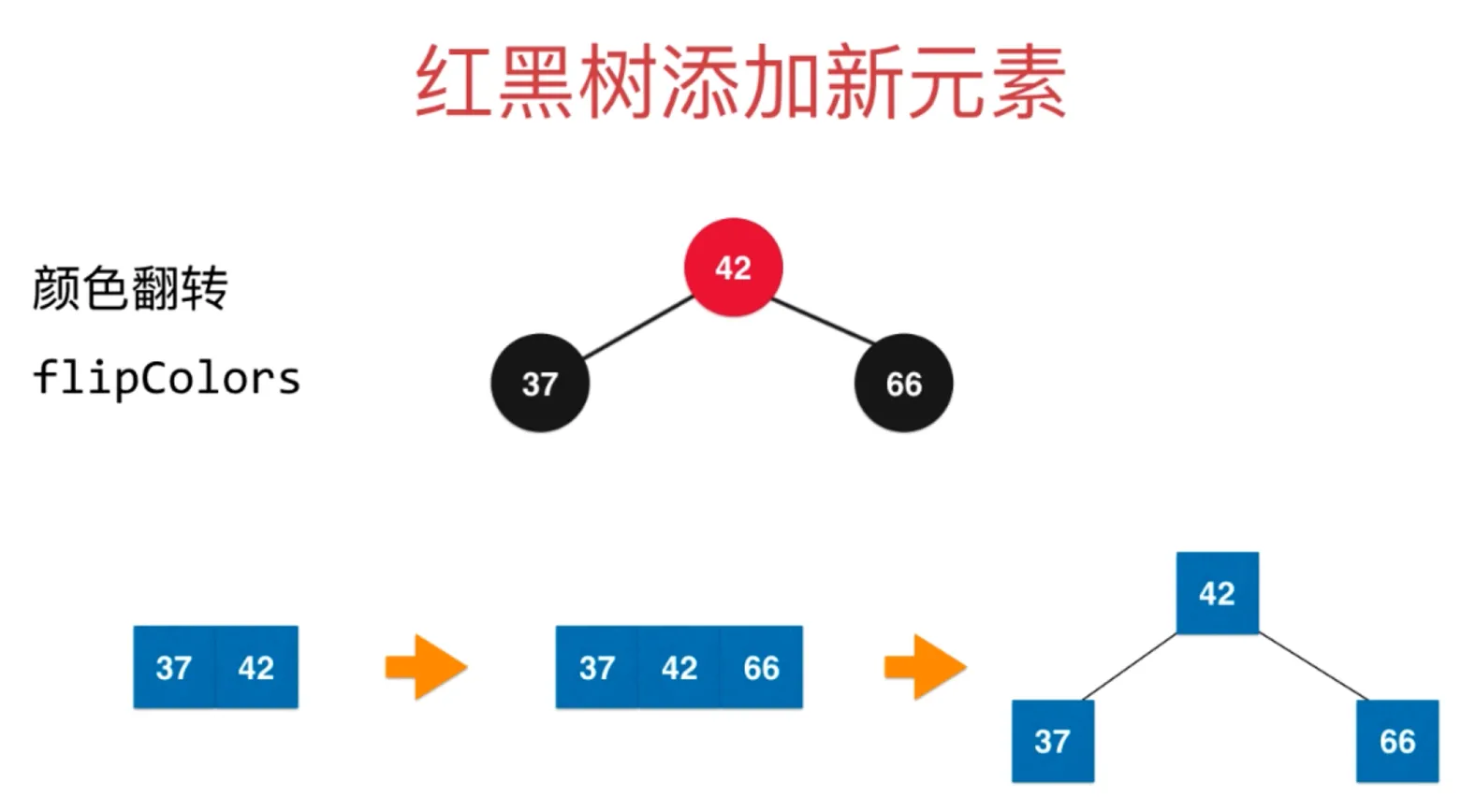
添加节点 12,此时放在左边
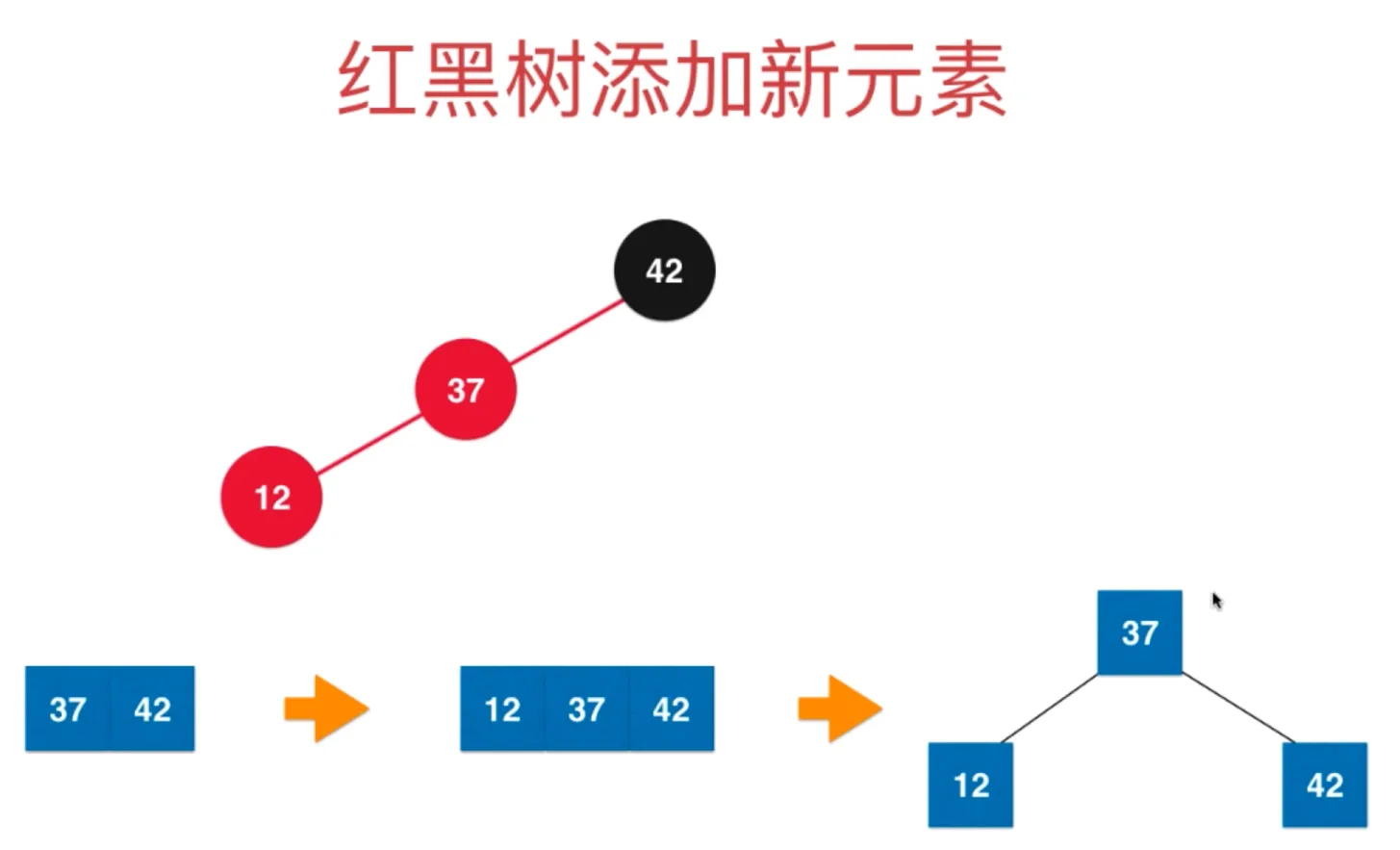 拆分为三个节点,需要右旋转
拆分为三个节点,需要右旋转
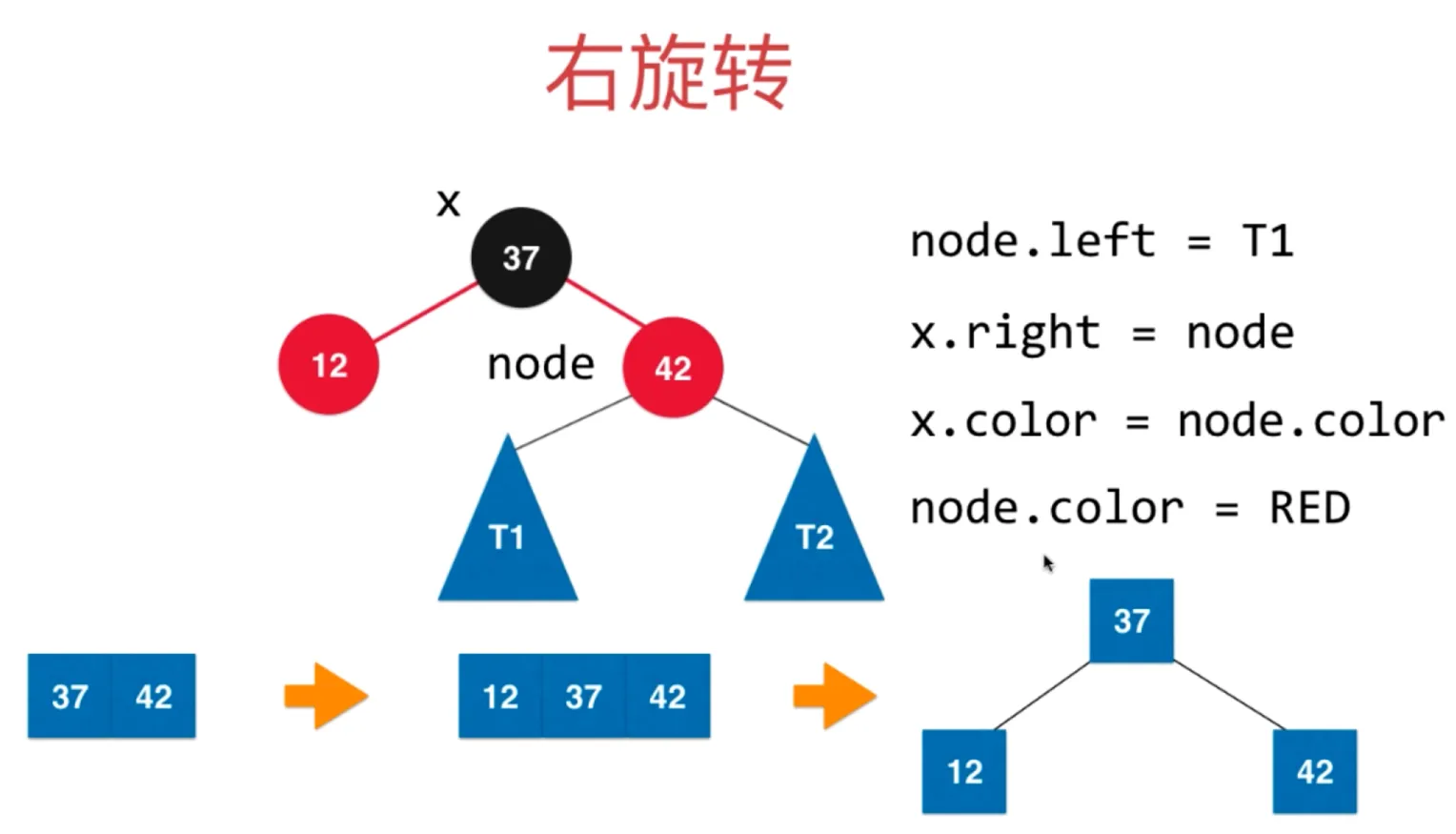 颜色翻转
颜色翻转
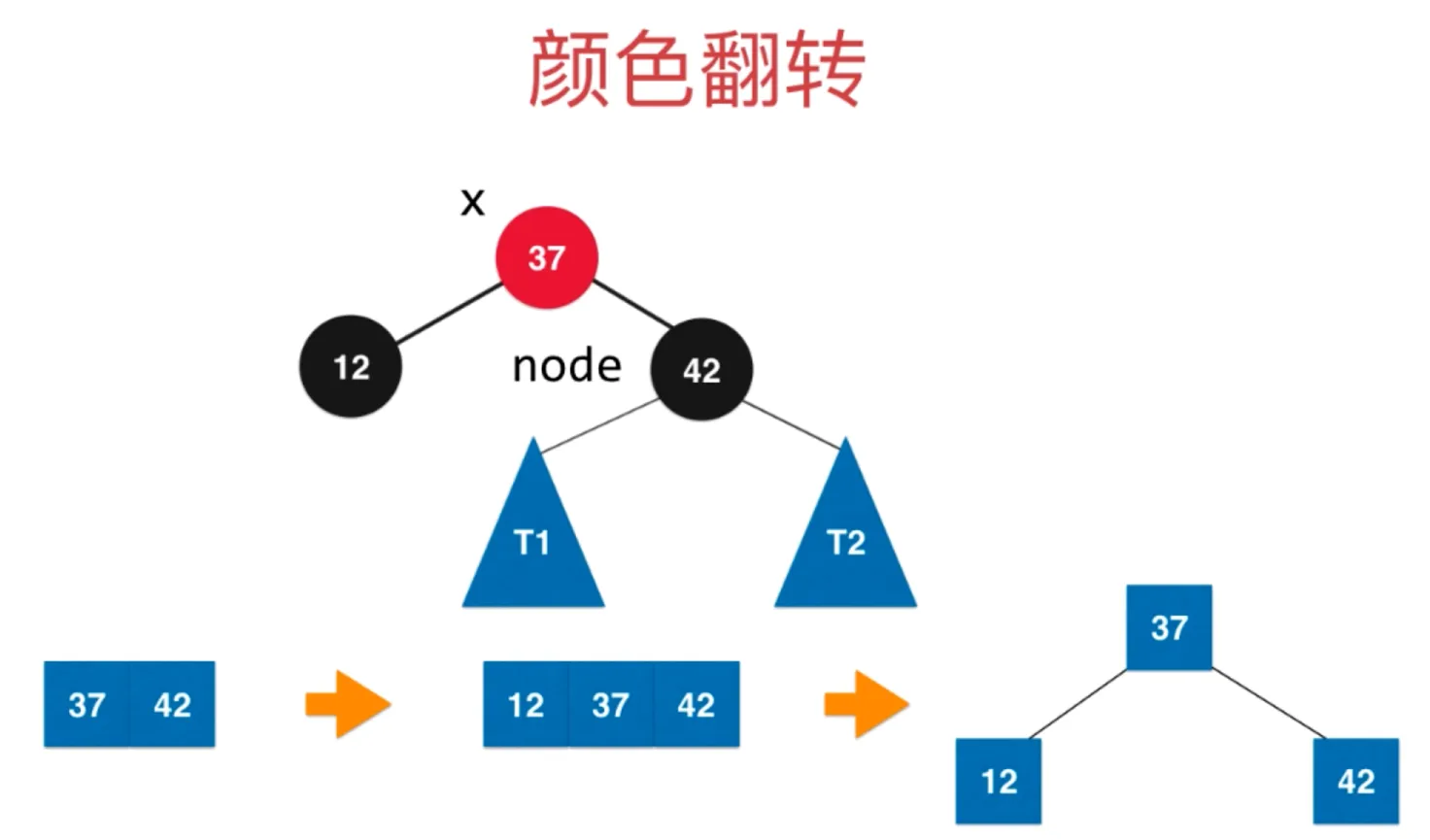
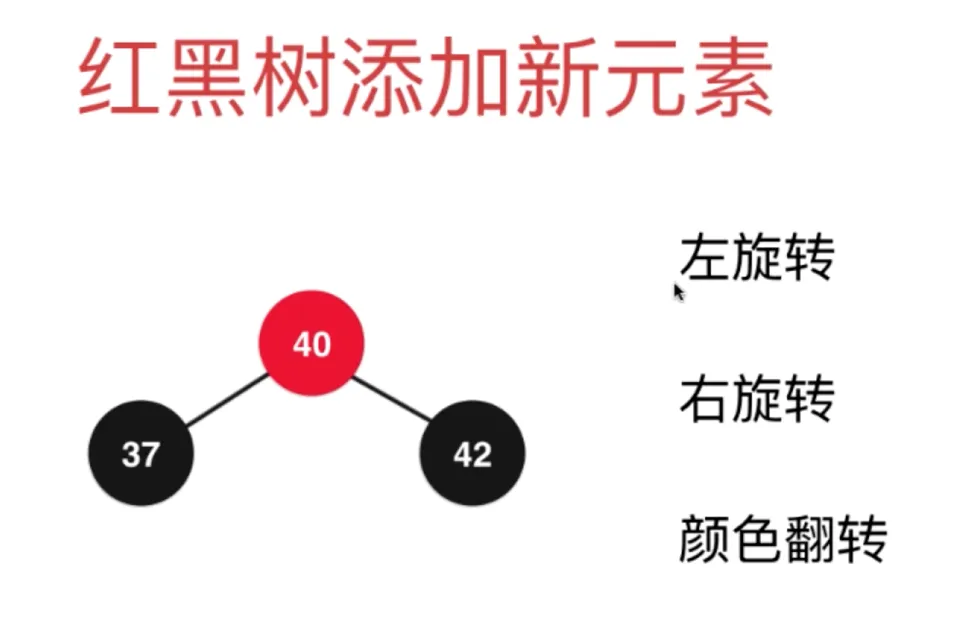
添加节点 40
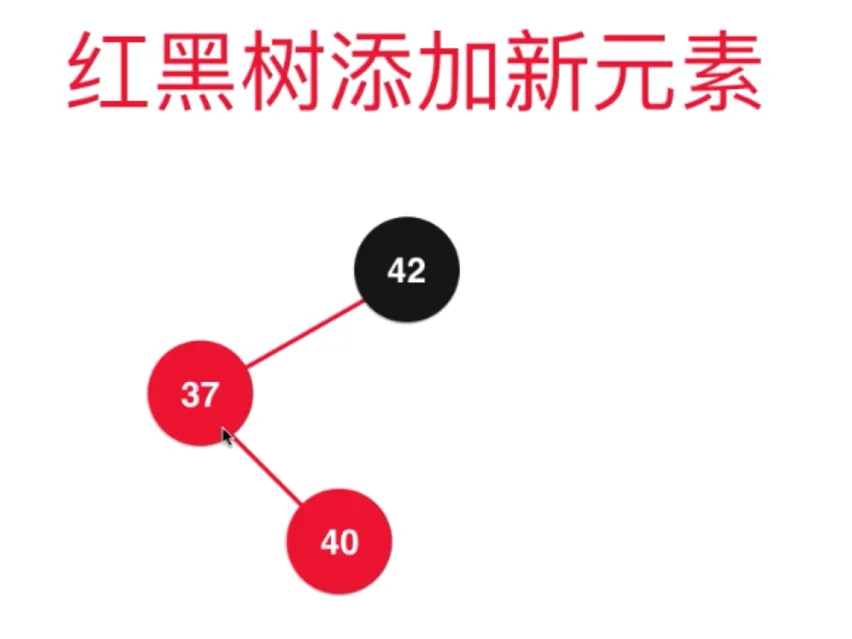 对节点 37 左旋转
对节点 37 左旋转
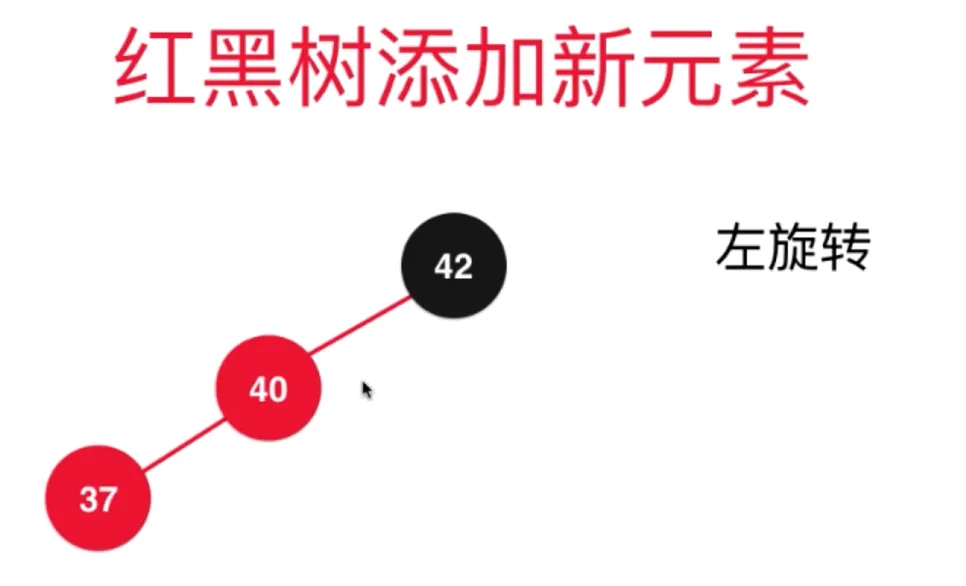 对节点 42 右旋转
对节点 42 右旋转
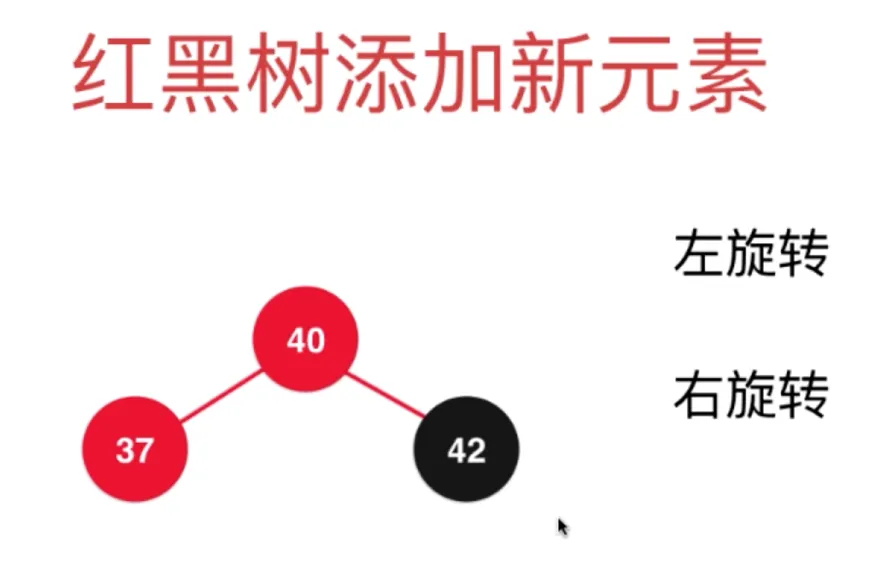 颜色翻转
颜色翻转

哈希表
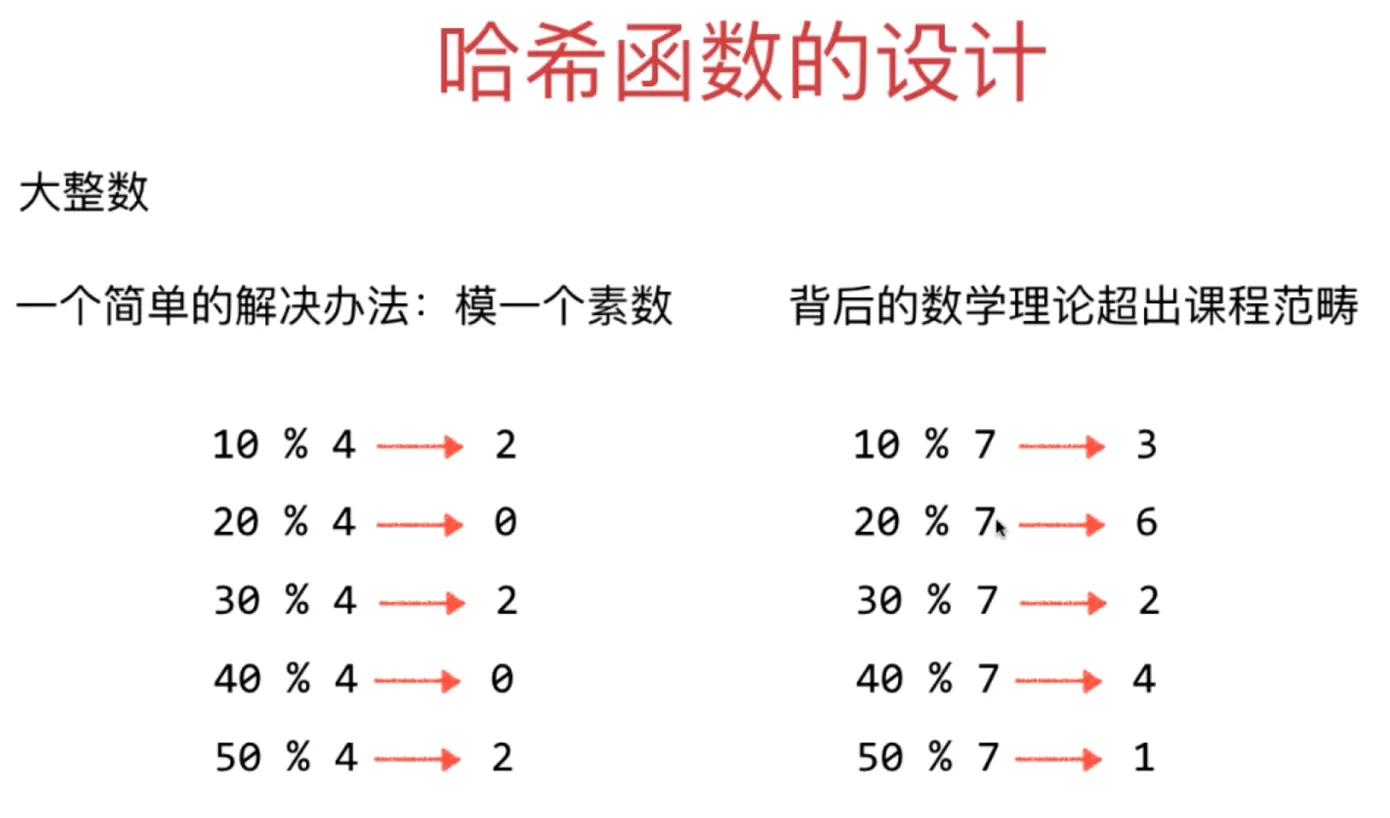
哈希函数的设计
大整数
一个简单的解决方法:模一个素数
https://planetmath.org/goodhashtableprimes
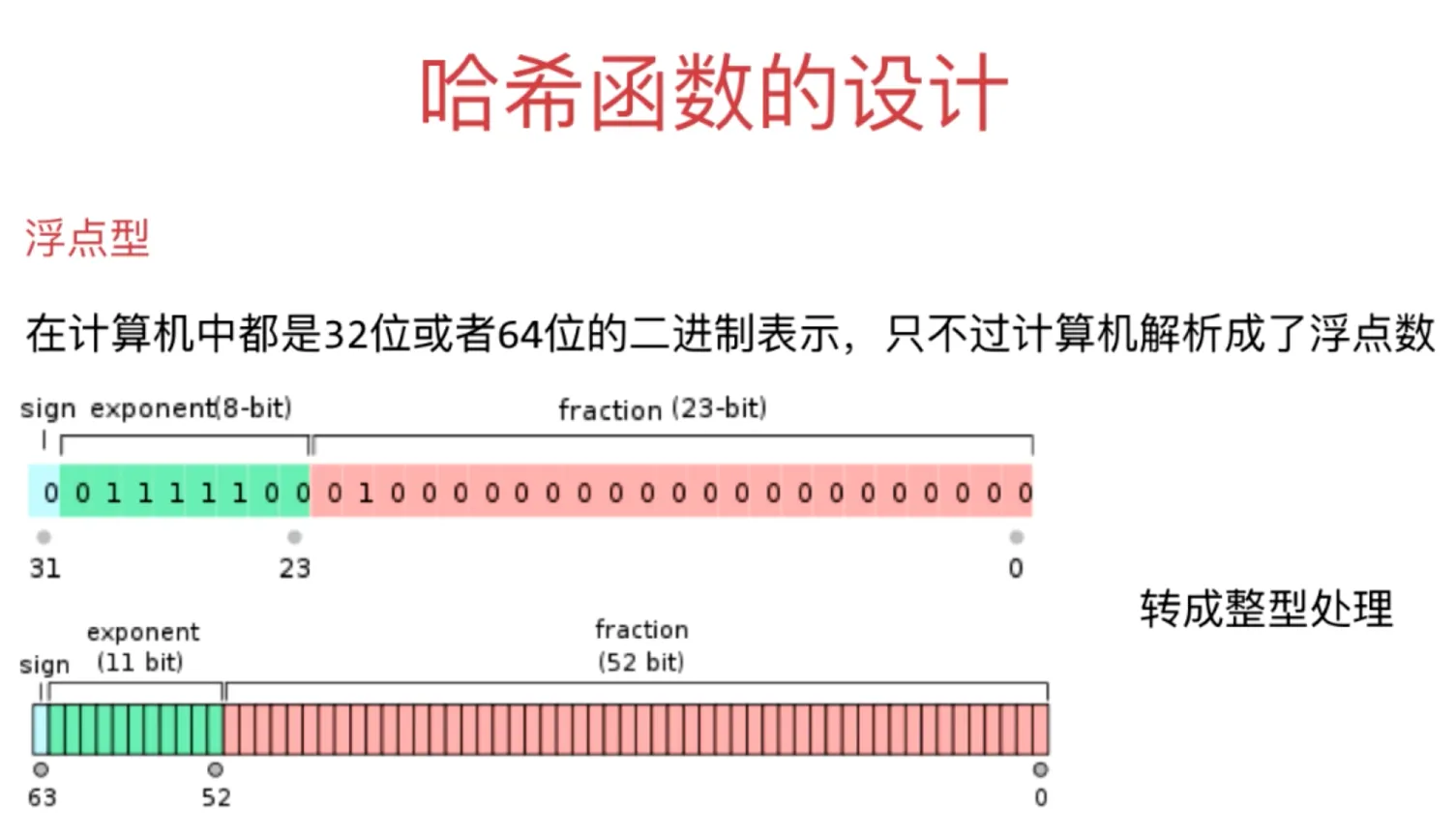
浮点型
转成整型处理
字符串 转成整型处理




哈希冲突的处理 链地址法
(hashCode(k1) & 0x7fffffff) % M
(和 0x7fffffff 按位与相当于是把符号位设置成 0)

哈希冲突的处理 开放地址法
如果哈希重复,向后+1,寻找空闲位置写入(线性探测) 此外还有平方探测 +2 + 4 +8 +16 二次哈希 (使用另一个哈希函数再次哈希) + hash2(key)
扩容根据指标 — 负载率(已经存入元素/总容量)达到某个阈值(如0.75)扩容
更多冲突处理方式 再哈希法 Rehashing Coalesced Hashing
SQRT 分解

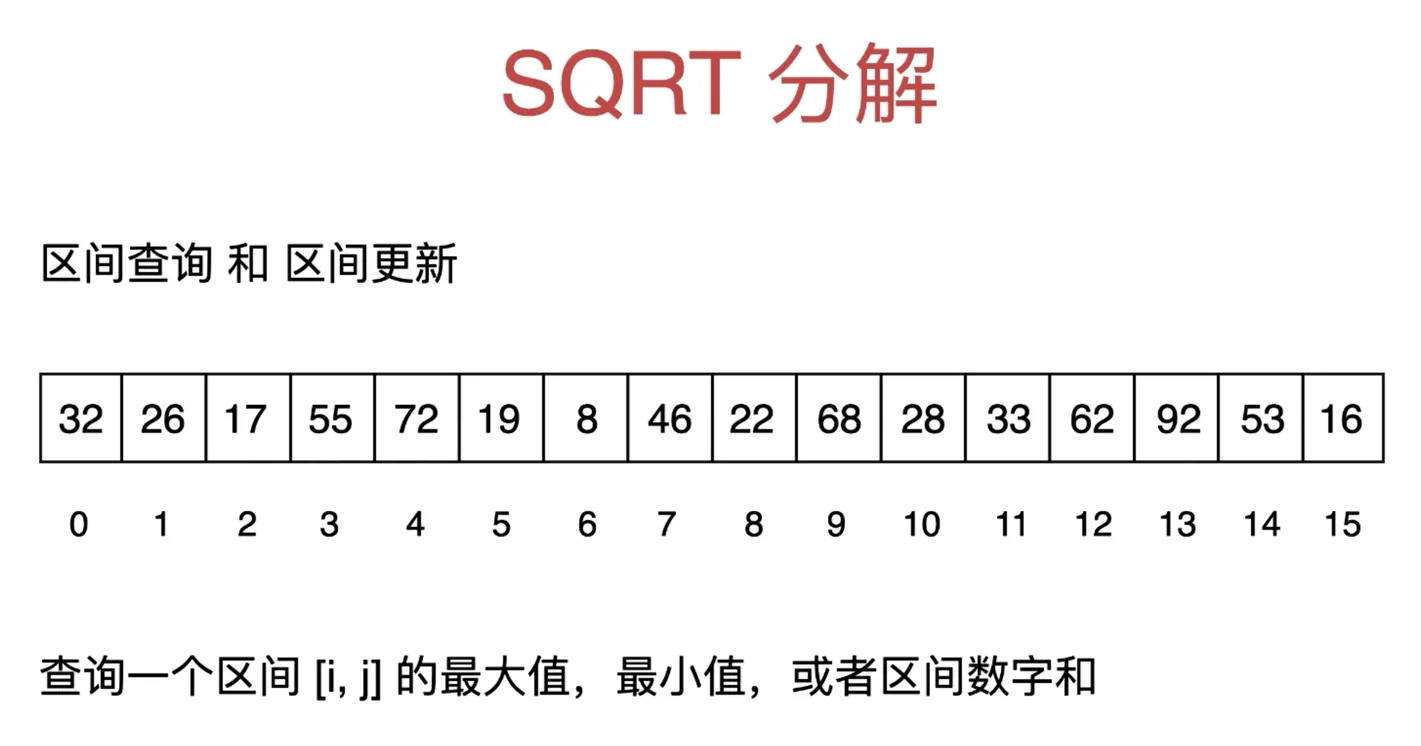
SQRT 分解区间查询
基本思想:把一个含有 N 个元素的数组分成 √n 份
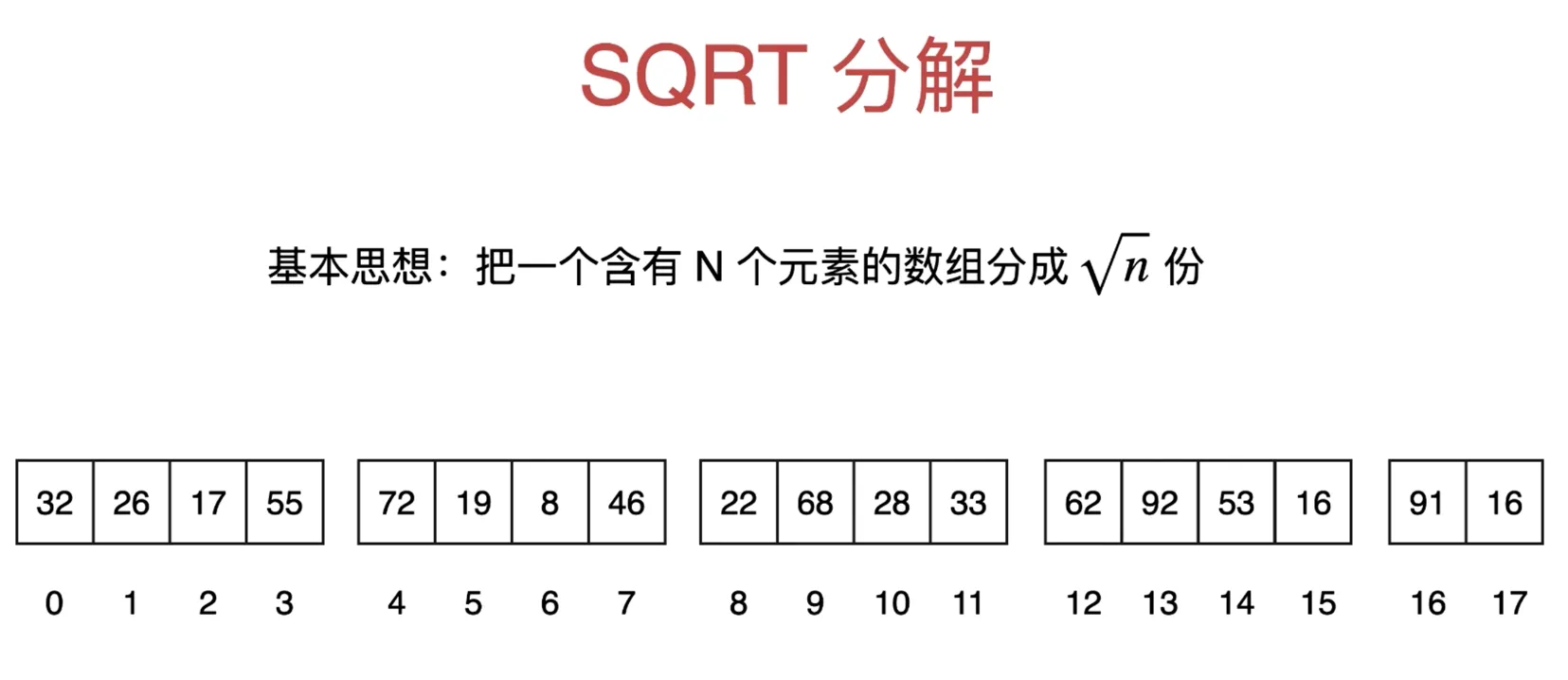 然后计算每一组的和
当查询的左右端点都在同一组时,比如查询
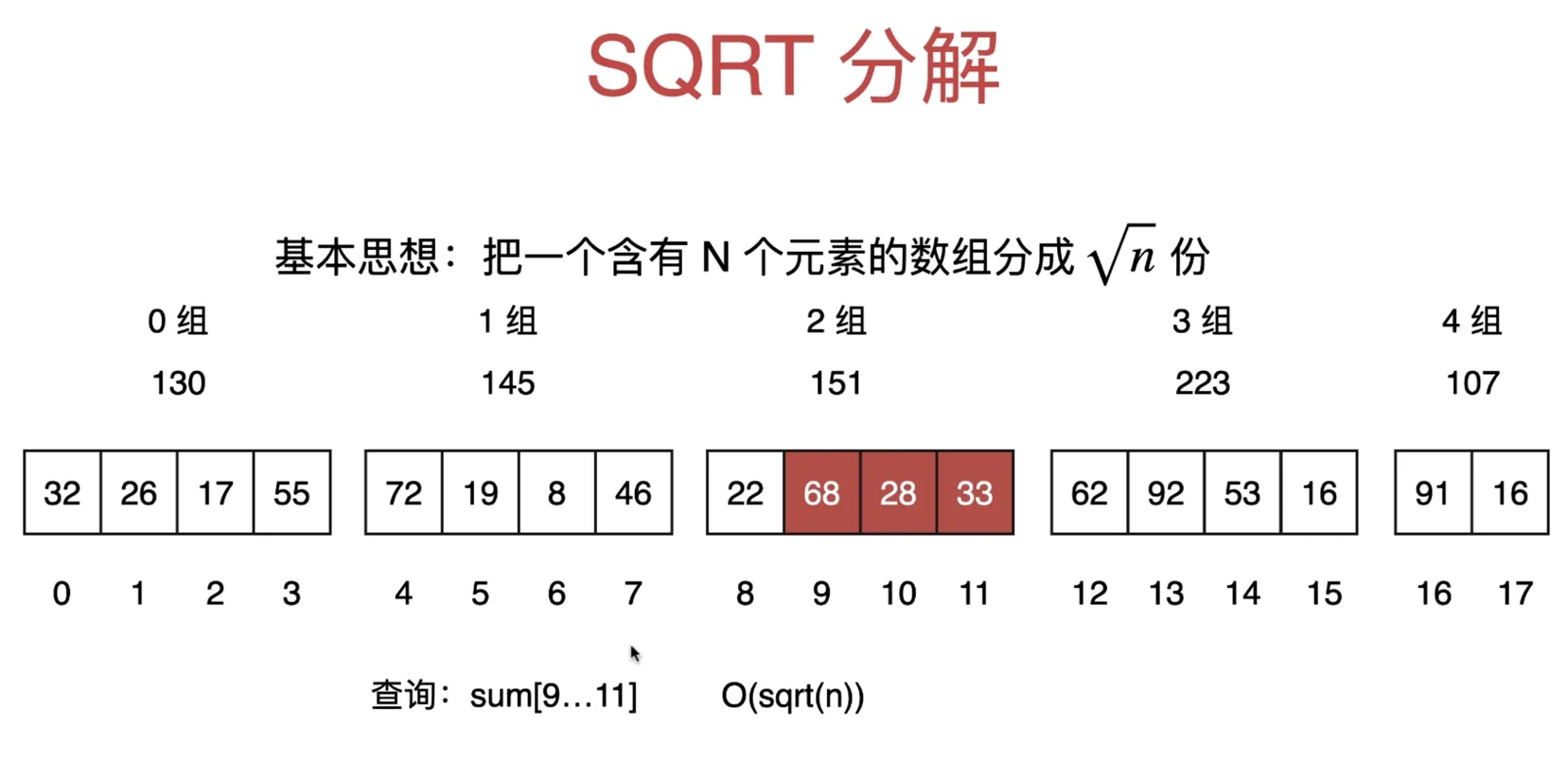
然后计算每一组的和
当查询的左右端点都在同一组时,比如查询 sum[9..11], 9/4 = 2 11/4=2, 都在 2 组, 计算和即可遍历从 复杂度 O(sqrt(n))
 当查询的左右端点不在同一组时,比如查询
当查询的左右端点不在同一组时,比如查询 sum[6...9], 端点在 1 组和 2 组,相连的,遍历从 6-9,求和,复杂度 O(sqrt(n))
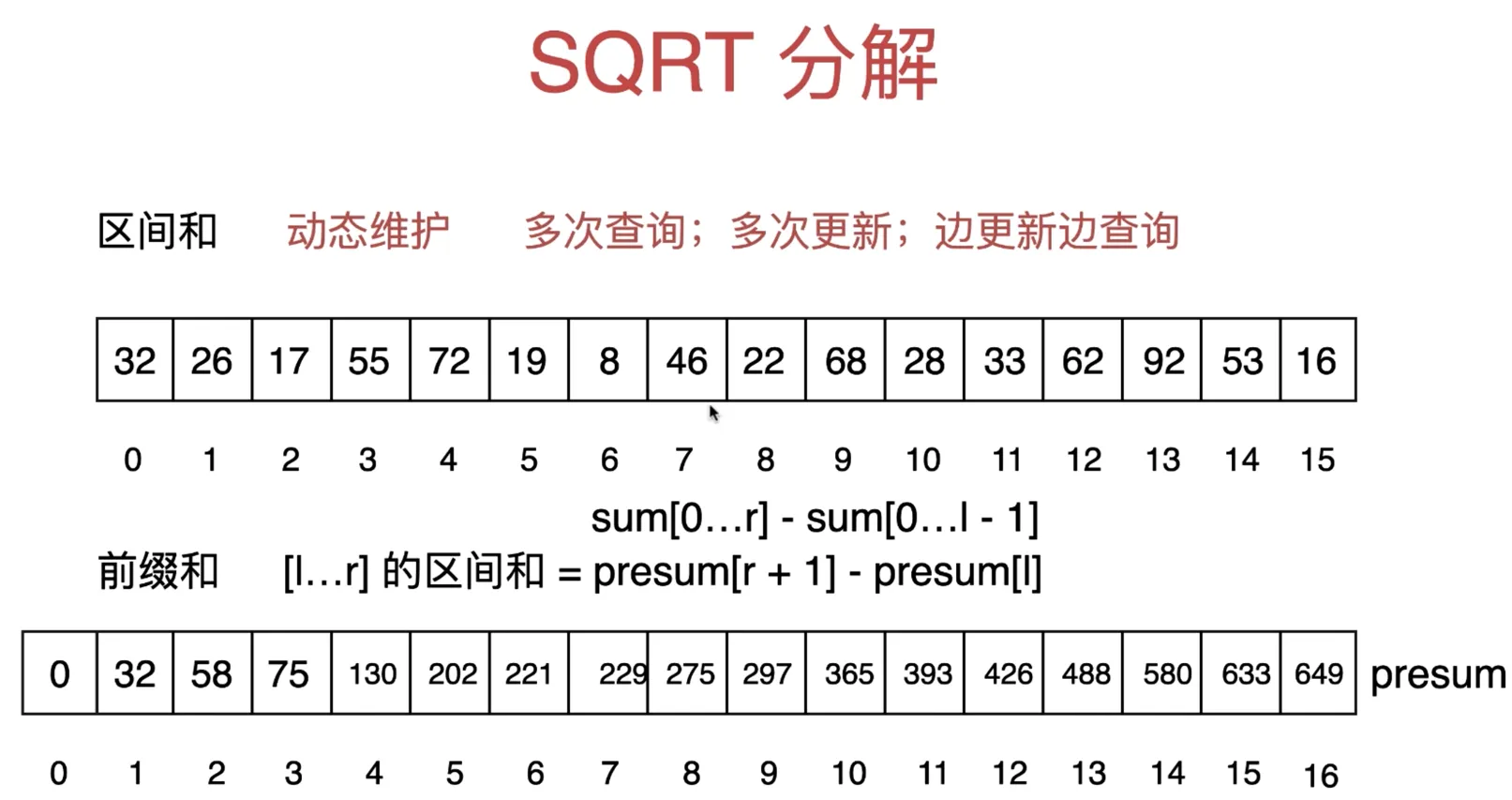
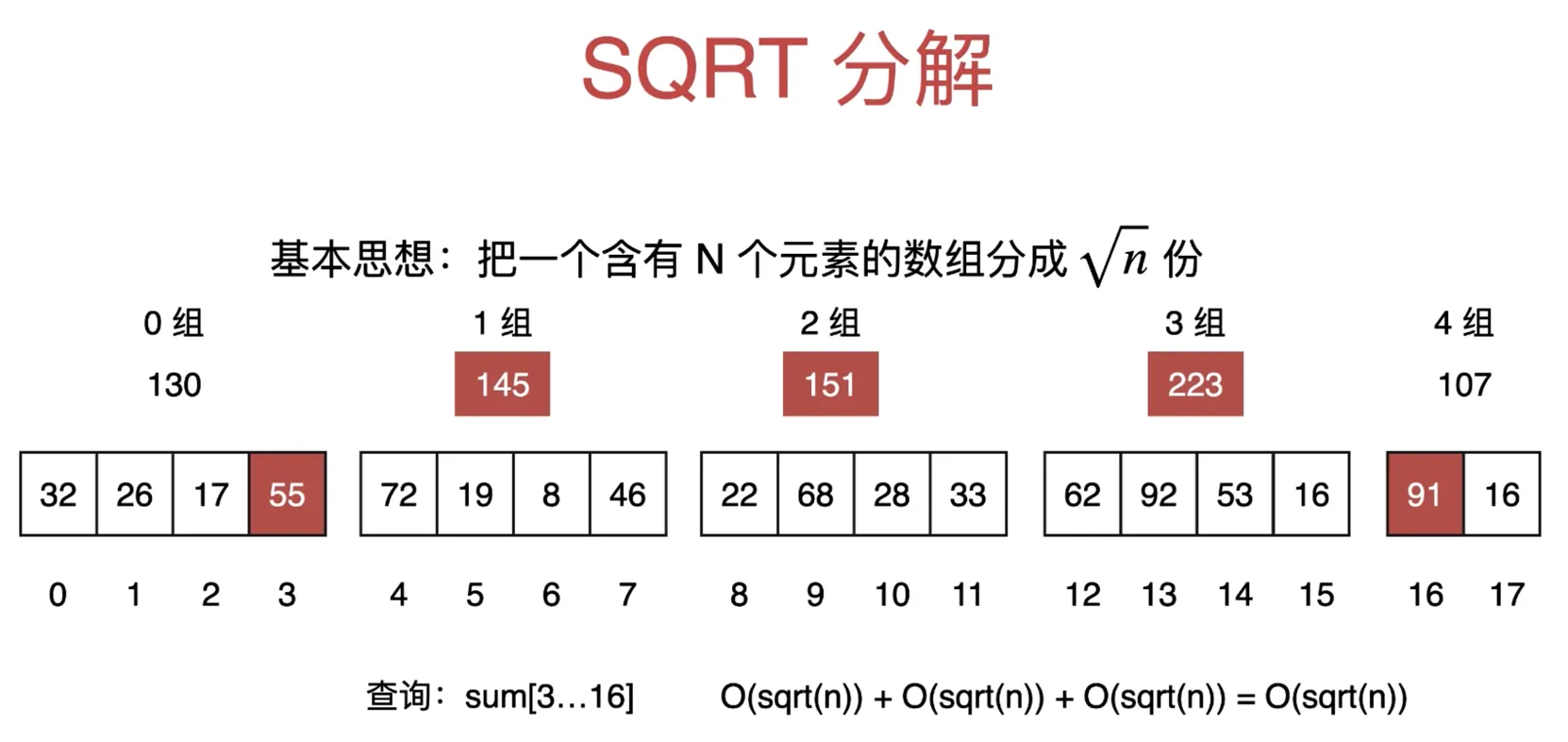
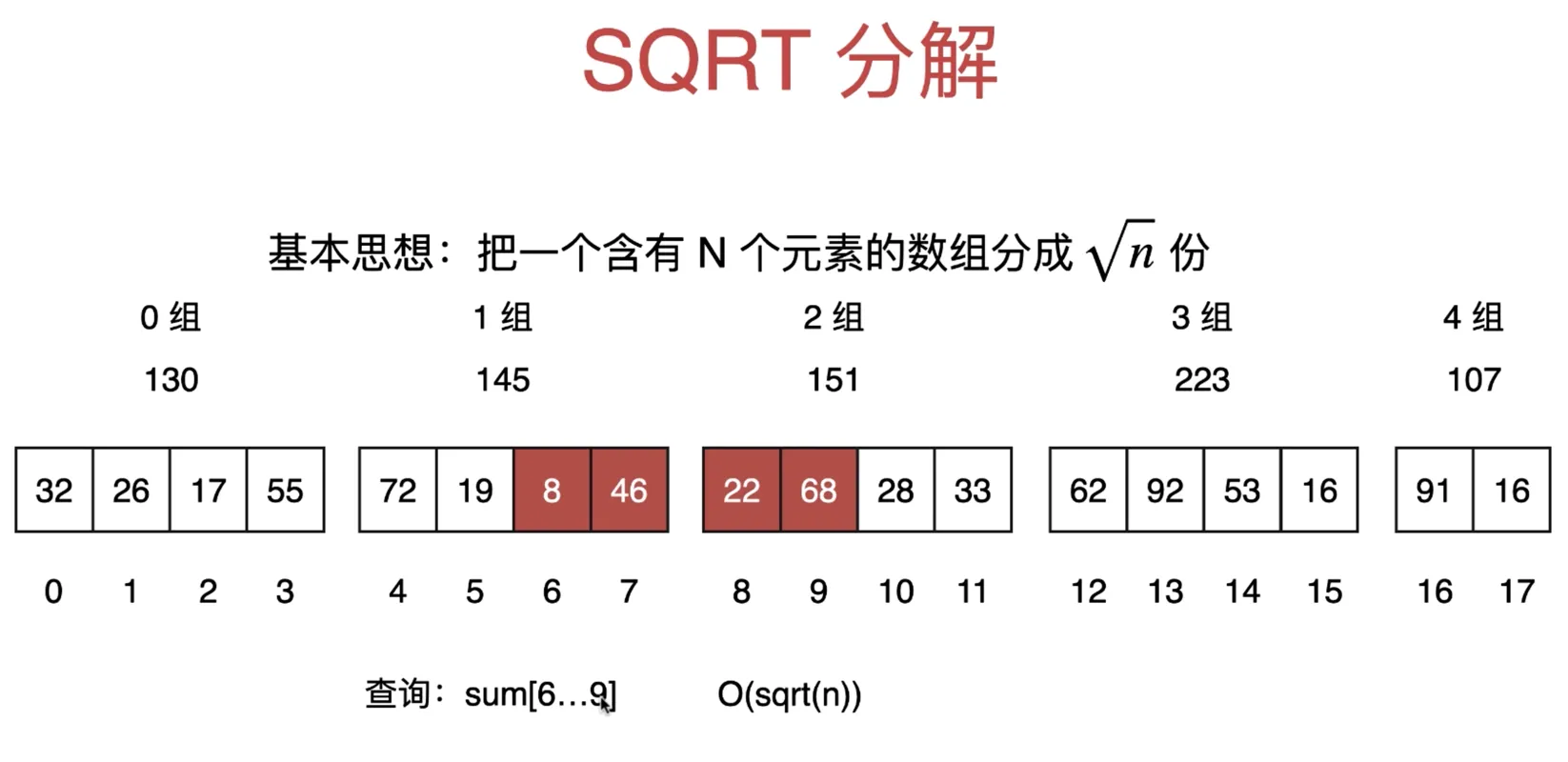 查询
查询 sum[3...16], sum(3) + 预处理的区间和 + sum(16),复杂度 O(sqrt(n))
SQRT 分解的单元素更新
update: data[6] = 66
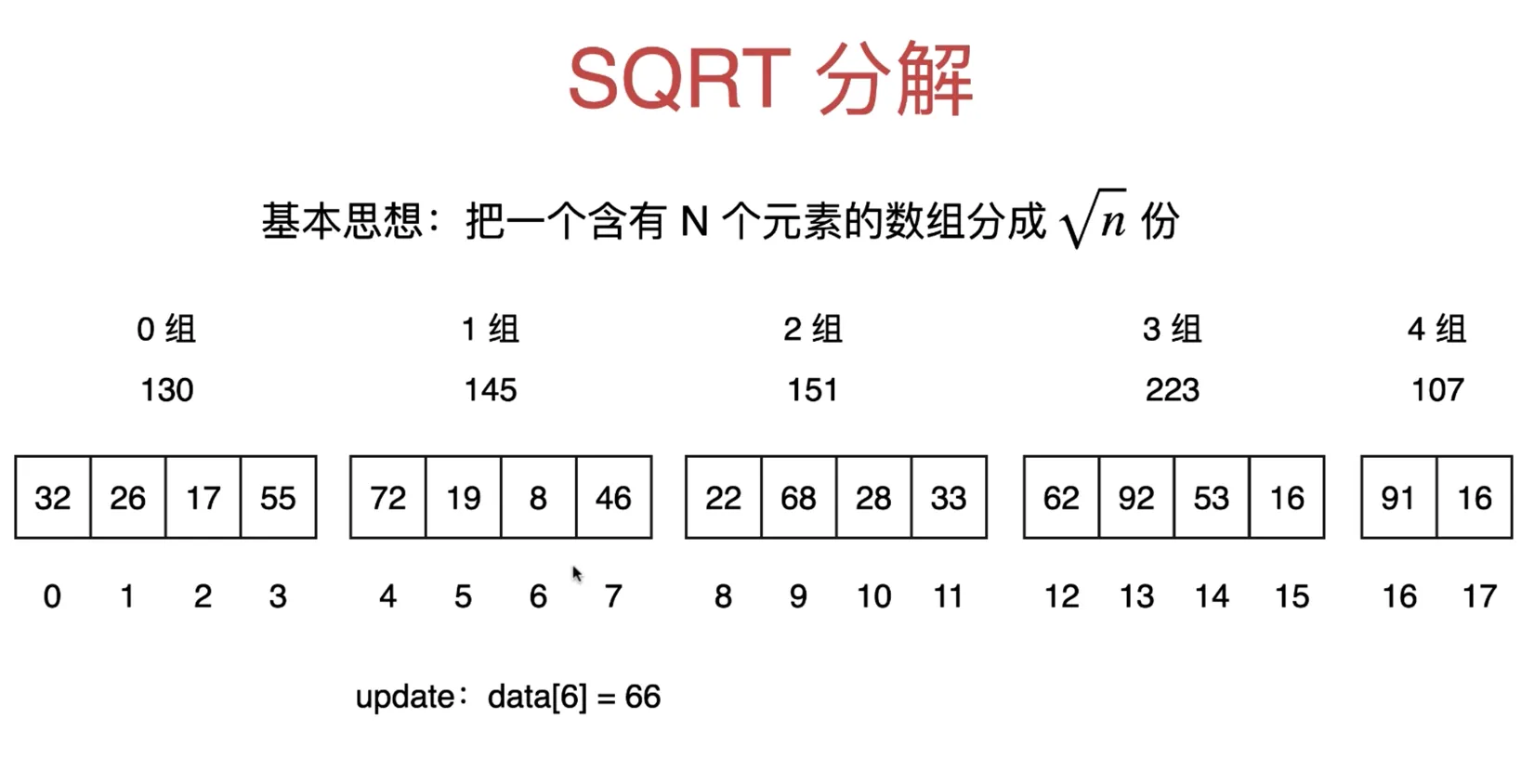
- 直接更新原始数组中 6 索引值为 66
重新计算这个区间的和,用原来的区间和 - 原来元素值 + 新的值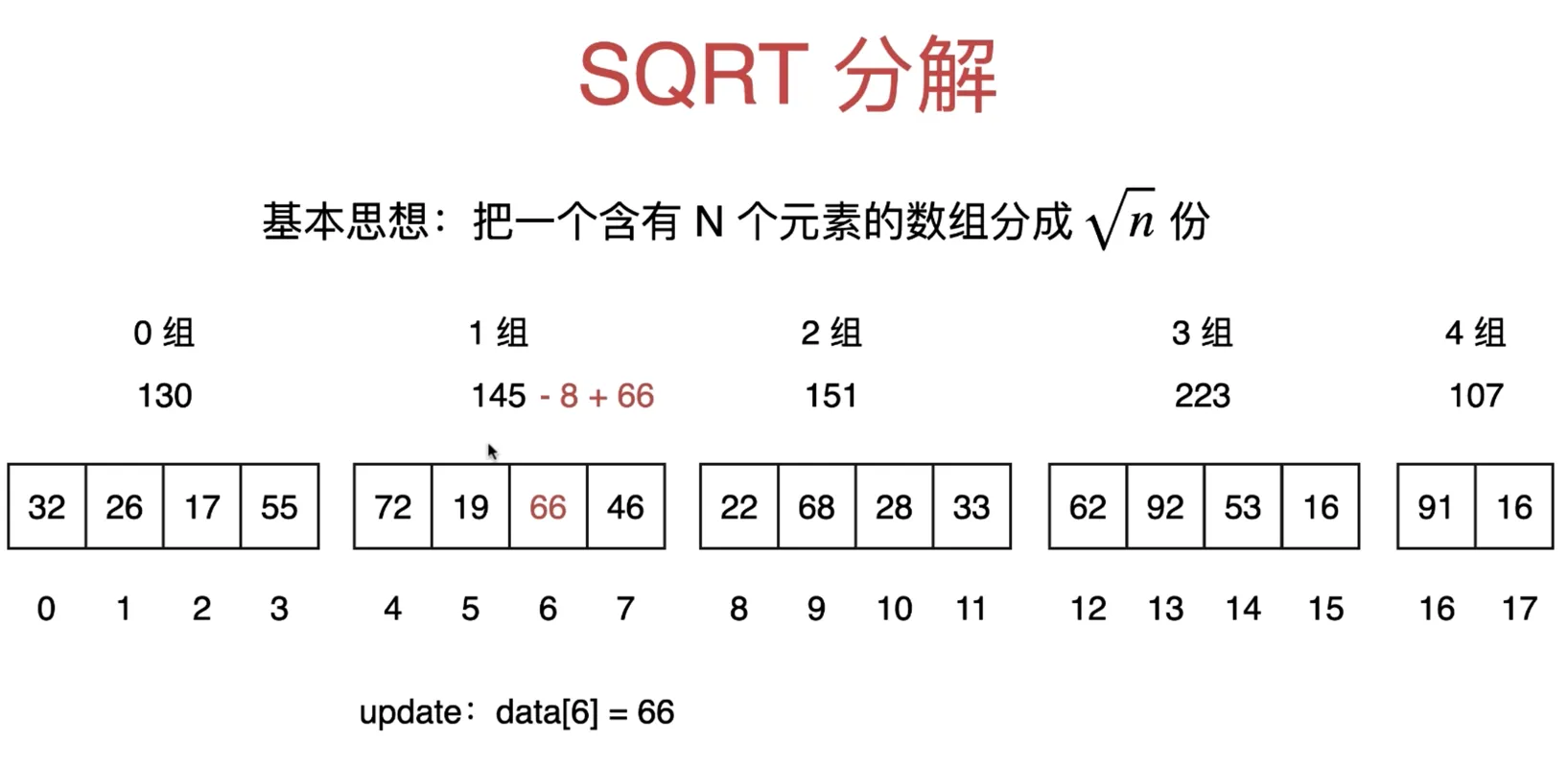
package SQRT;
import java.util.Arrays;
// LeetCode 303 307
public class NumberArray {
private int[] data, blocks;
private int N; // 元素总数
private int B; // 每组元素个数
private int Bn; // 组数
public NumberArray(int[] nums) {
N = nums.length;
if (N == 0) {
return;
}
B = (int) Math.sqrt(N);
Bn = N / B + (N % B == 0 ? 0 : 1);
data = Arrays.copyOf(nums, N);
blocks = new int[N];
for (int i = 0; i < N; i++) {
blocks[i / B] += data[i];
}
}
public int sumRange(int x, int y) {
if (x < 0 || x >= N || y < 0 || y >= N || x > y) {
return 0;
}
int bstart = x / B;
int bend = x % B;
int res = 0;
if (bstart == bend) {
for (int i = x; i <= y; i++) {
res += data[i];
}
return res;
}
for (int i = x; i < (bstart + 1) * B; i++) {
res += data[i];
}
for (int b = bstart + 1; b < bend; b++) {
res += blocks[b];
}
for (int i = bend * B; i <= y; i++) {
res += data[i];
}
return res;
}
public void update(int i, int val) {
if (i < 0 || i >= N) {
return;
}
int oldVal = data[i];
int b = i / B;
blocks[b] -= oldVal;
blocks[b] += val;
data[i] = val;
}
}非比较排序算法
不是元素之间不能比较,而是不借助 compareTo 主要应用于字符串排序
计数排序
LeetCode 75: 颜色分类 给定一个数组,只包含 0,1,2,对数组排序
之前使用三路快排来实现
假设有 cnt0 个 0; cnt1 个 1; cnt2 个 2;
|--cnt0 个 0--|--cnt1 个 1--|--cnt2 个 2--|
|-------------|-------------|------------|
0 cnt0 cnt1+cnt2 n
[l, r1] 区间有 r1 - l + 1 个元素
[l, r2) 区间有 r2 - l 个元素public void setColors(int[] nums) {
int[] cnt = new int[3];
for (int num : nums) {
cnt[num]++;
}
// 对 nums 排序,前中后 0 1 2
for (int i = 0; i < cnt[0]; i++) {
nums[i] = 0;
}
for (int i = cnt[0]; i < cnt[0] + cnt[1]; i++) {
nums[i] = 1;
}
for (int i = cnt[0] + cnt[1]; i < cnt[0] + cnt[1] + cnt[2]; i++) {
nums[i] = 2;
}
}注:cnt 的数组中,下标代表 nums 中的元素值(当前只有 0,1,2)三种元素,每一项存储了 nums 中值为 i 的数量之和
当前代码的局限性
只能处理 0,1,2 这三种元素
int[] cnt = new int[3];
for(int num : nums) {
cnt[num]++;
}如果数字的可能范围是 [0, R)
那么可以改写为 int[] cnt = new int[R]
计数排序需要的空间:O(R) 只适用小数据范围
如果数字的可能范围是 [L, R]
int[] cnt = new int[R-L+1]
cnt[num-L]++
如果取值范围是[0, 101), 不可能写 101 个 for 循环
总结 cnt 和 index 对应关系
0: [0, cnt[0])
1: [cnt[0], cnt[0] + cnt[1])
2: [cnt[0] + cnt[1], cnt[0] + cnt[1] + cnt[2])
3: [cnt[0] + cnt[1]+ cnt[2], cnt[0] + cnt[1] + cnt[2]+ cnt[3])
可以看到,排序就是
把 [0, cnt[0]) 设置为 0
把 [cnt[0], cnt[0] + cnt[1])) 设置为 1
把 [cnt[0] + cnt[1], cnt[0] + cnt[1] + cnt[2]) 设置为 2
…… 0 1 2 3
cnt 2 3 5 6
index 0 2 5 10 16
新开辟数组 index, 把 [index[i], index[i+1]) 区间的值为 i
index 中值的计算
index[1] = index[0] + cnt[0] (0+2=2)
index[2] = index[1] + cnt[1] (2+3=5)
index[3] = index[2] + cnt[2] (5+5=10)
……
public class Solution {
public void setColors(int[] nums) {
// 处理元素取值范围是 [0, R) 的计数排序
int R = 3;
int[] cnt = new int[R];
for (int num : nums) {
cnt[num]++;
}
// [index[i], index[i + 1]) 的值为 1
int[] index = new int[R + 1];
index[0] = 0;
for (int i = 0; i < R; i++) {
index[i + 1] = index[i] + cnt[i];
}
for (int i = 0; i < index.length - 1; i++) {
for (int j = index[i]; j < index[i + 1]; j++) {
nums[j] = i;
}
}
}
}